Всем привет!
Надеюсь все уже успели оправиться от революции цветов и званий и даже, может быть, попробовать написать раунд в новом для себя положении. Последний раунд собрал космическое количество народу: 8000 человек! И, не побоюсь это сказать, с технической точки зрения раунд прошёл без малейших нареканий! Будем считать, что 15-минутный перенос контеста был частью нашего хитрого плана по достижению рекорда :)
Спешим сообщить, что команда Codeforces способна не только подкручивать цвета и формулы, но и постоянно работать над развитием проекта.
Зайдя на страницу с соревнованиями, вы можете теперь видеть список авторов каждого из раундов! Более того, в профиле у человека теперь есть пункт "проблемсеттинг", по которому можно посмотреть на список всех контестов, к подготовке которых человек имел отношение.
Endagorion, например, выглядит так.









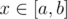 в дереве функция
в дереве функция  подсчётов градиента мы практически научились решать задачу. Осталось только понять, где именно расположен ответ. Заметим, что глобальный оптимум, скорее всего, окажется внутри какого-то ребра. Тогда, как нетрудно видеть, оптимальной вершиной является один из концов этого ребра, а именно, одна из двух последних рассмотренных в процессе нашего алгоритма вершин. В какой именно можно определить, явно вычислив значение функции в них и взяв меньшее.
подсчётов градиента мы практически научились решать задачу. Осталось только понять, где именно расположен ответ. Заметим, что глобальный оптимум, скорее всего, окажется внутри какого-то ребра. Тогда, как нетрудно видеть, оптимальной вершиной является один из концов этого ребра, а именно, одна из двух последних рассмотренных в процессе нашего алгоритма вершин. В какой именно можно определить, явно вычислив значение функции в них и взяв меньшее. .
.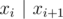 для (
для (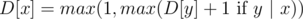 по всем
по всем 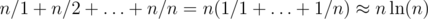 .
.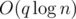 .
. 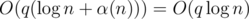 .
.



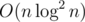 , получите виртуальную медаль!
, получите виртуальную медаль!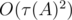 , где
, где 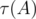 — количество делителей числа
— количество делителей числа 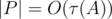 ). Значит, общая сложность решения —
). Значит, общая сложность решения — 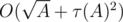 .
.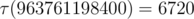 . Полезная оценка, не являющаяся, тем не менее, точной асимптотикой, заключается в том, что
. Полезная оценка, не являющаяся, тем не менее, точной асимптотикой, заключается в том, что 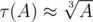 )
)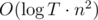 . А потом до
. А потом до 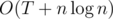


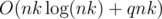 или
или 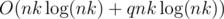 . Для каждой возможной суммы денег
. Для каждой возможной суммы денег 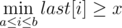 . Это значит, что для хранения величины last можно воспользоваться деревом отрезков. Аналогично проверяем для столбцов. Выходит решение, отвечающее на все запросы off-line за время
. Это значит, что для хранения величины last можно воспользоваться деревом отрезков. Аналогично проверяем для столбцов. Выходит решение, отвечающее на все запросы off-line за время 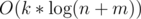 .
.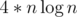 running time. But unfortunately the statement contained wrong constraints, so we reduced input size during the tour. Nevertheless, we will add the harder version of this task and you will be able to submit it shortly.
running time. But unfortunately the statement contained wrong constraints, so we reduced input size during the tour. Nevertheless, we will add the harder version of this task and you will be able to submit it shortly.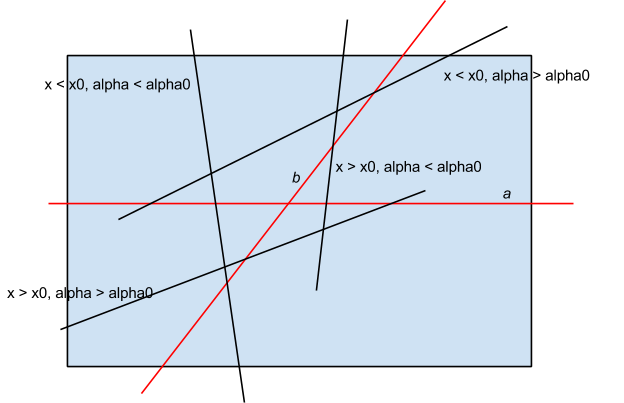
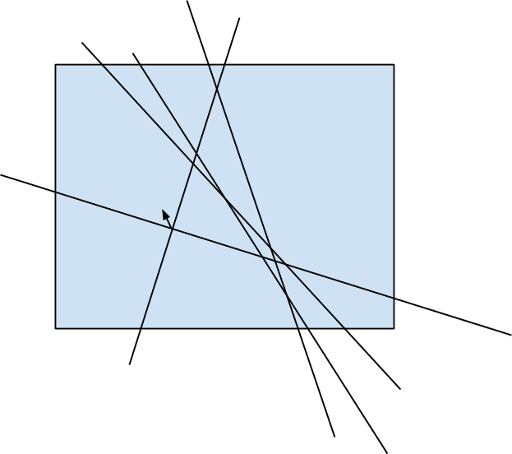
 by fixing the first side of the angle and then adding lines in ascending order of polar angle, and then by keeping the number of lines that intersect the base line to the left and that intersect the base line to the right. Key idea is that the exact of four angles formed by the pair of lines
by fixing the first side of the angle and then adding lines in ascending order of polar angle, and then by keeping the number of lines that intersect the base line to the left and that intersect the base line to the right. Key idea is that the exact of four angles formed by the pair of lines 

