Hello Codeforces,
This is the second blog on the series about the applications of the rotating calipers technique. If you haven't read the first part yet, make sure to check it out, as much of the terminology that was introduced throughout the first part is going to be used here without further explanation. In this blog, a few more advanced applications will be presented.
Short recap of the main terminology
- Line of support: a line $$$l$$$ that intersects the boundary of the polygon such that the entire polygon lays on one side of $$$l$$$
- Anti-podal pair: a pair of vertices which have two parallel lines of support intersecting them
- Rotating calipers: an algorithm where parallel lines of support get rotated around the polygon while being kept on the boundary of the polygon at all times
Minimum-area enclosing rectangle of a convex polygon
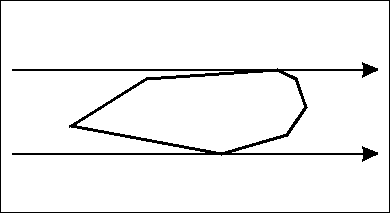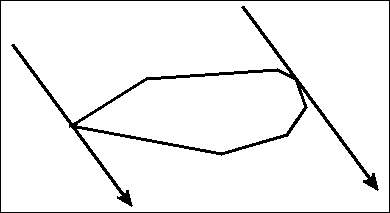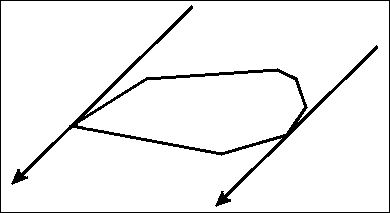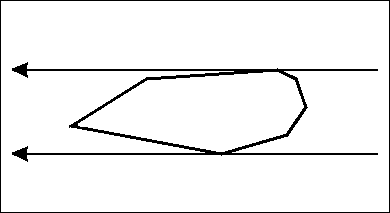
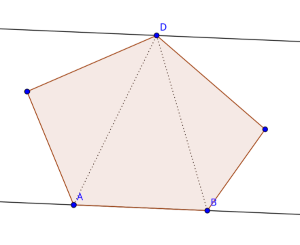
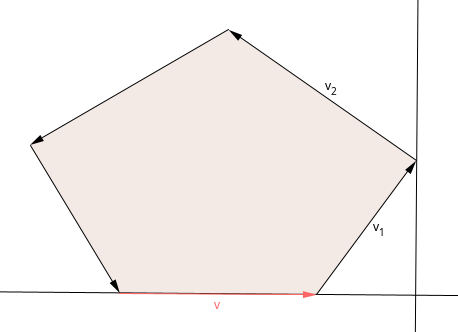
The first application that is going to be discussed is the minimum area enclosing rectangle problem. For a given polygon $$$P$$$, the problem asks us to find a minimum area rectangle $$$R$$$ such that all points of the polygon are inside that rectangle. It is quite clear why all 4 sides of the rectangle must lay on the boundary of $$$P$$$. However, an even stronger result can be obtained: If the area is minimum, then one of the sides of the rectangle has to intersect an edge of the polygon. To understand why, consider the contrary scenario: each side of the rectangle $$$R$$$ intersects with exactly one vertex of $$$P$$$, and the area of $$$R$$$ is still minimum possible. Let's call these vertices $$$p_a$$$, $$$p_b$$$, $$$p_c$$$, $$$p_d$$$, in clockwise order. $$$R$$$ has side lengths $$$l_1$$$ and $$$l_2$$$ respectively. An example of what this can look like:
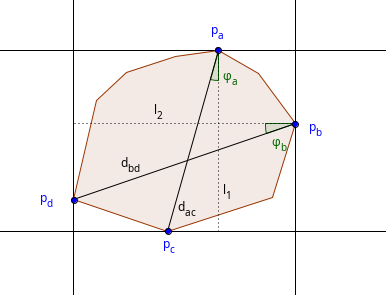
The area of the rectangle is $$$A = l_1 \times l_2$$$. Rotating the rectangle by a small angle $$$ \theta $$$ changes the side lengths of the rectangle. What happens usually is that there exists a direction of rotation where $$$l_1$$$ increases, and another direction where $$$l_1$$$ decreases. There are two possible scenarios of what might happen:
- There exists a direction of rotation which allows both $$$l_1$$$ and $$$l_2$$$ to be decreased.
- One direction of rotation would increase $$$l_1$$$ and would decrease $$$l_2$$$, and vice versa.
In the first case, it is clear that a rotation would result in a lower total area. However, for the second case, it isn't as clear why it is possible to get a smaller area. So, without loss of generality we will assume that $$$\varphi_{a} > \varphi_{b}$$$ and we rotate the polygon by $$$\theta$$$ degrees. The following also holds true:
Rotating by $$$\theta$$$ degrees would change last equation into:
To see why $$$A' < A$$$, we have to take a look at the cosine function for values between $$$0$$$ and $$$ \frac{\pi}{2}$$$:
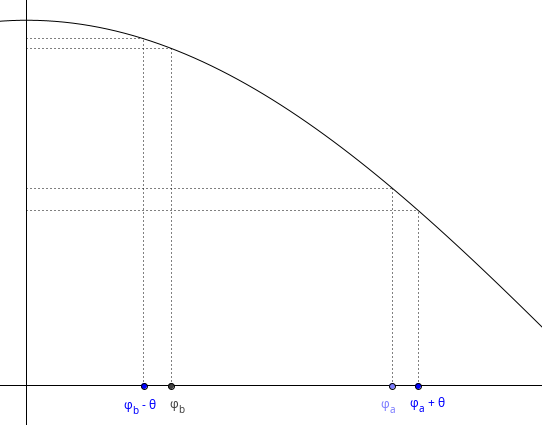
We can see that $$$cos(\varphi_a + \theta )$$$ got closer to 0 than $$$cos(\varphi_b -\theta )$$$ got to 1. Therefore, the total area must have gotten smaller.
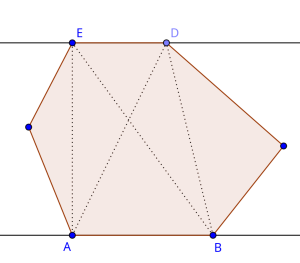
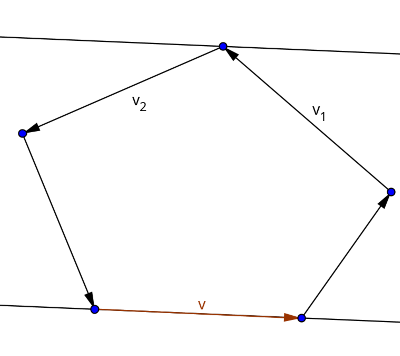
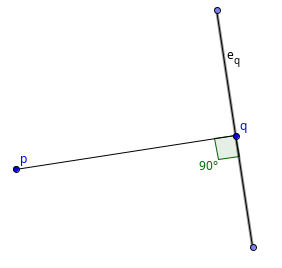
Now that we know that each minimum area enclosing rectangle touches at least one of the edges of the polygon, we can now use the rotating calipers technique to solve this problem. The only difference between the standard rotating calipers technique and this variation is that we maintain 4 lines instead of just two, and these 4 lines together must form an enclosing rectangle. Essentially, we are maintaining a "rotating rectangle" around the polygon. One of the main difficulties of the implementation would be the criteria on when to stop rotating because a $$$90^{\circ}$$$ degree has been reached. For that, we'll make use of the dot product. Take a look at the following image:
The following two properties hold true:
So, whenever there occurs a sign change in the dot product, we know that we can stop rotating further. The total runtime of this algorithm would be $$$O(4*n) \in O(n)$$$, since the enclosing rectangle contains 4 edges and maintaining them takes $$$O(n)$$$ steps each.
Minimum-perimeter enclosing rectangle
The minimum perimeter enclosing rectangle problem is very similar to the minimum-area version. Just as in the previous section, if the perimeter is minimum then at least one of the edges of $$$P$$$ must intersect with an edge of the rectangle. To see why this is the case, consider the opposite scenario. Define $$$p_i (1 \leq i \leq 4)$$$ to be the vertices that intersect with the rectangle. Also, define angles $$$\alpha_i$$$ and $$$\beta_i$$$ like this:
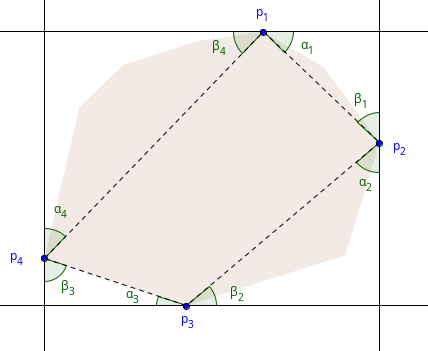
From the law of sines, we can conclude that the perimeter $$$p_m$$$ must be:
Let $$$\theta_{min} < 0 < \theta_{max}$$$ be the angles of rotation which make one of the edges of $$$P$$$ intersect with the rectangle. We can now reformulate the perimeter $$$p_m$$$ as a function with a variable $$$\theta \in [ \theta_{min}, \theta_{max} ]$$$, which represents the perimeter after we rotate the polygon by $$$\theta$$$ degrees:
Since $$$\alpha_i + \theta$$$ and $$$\beta_i - \theta$$$ are angles of a triangle, $$$|(\alpha_i + \theta) - (\beta_i - \theta)| \leq \frac{\pi}{2} $$$ must hold true. Each of the summands of $$$p_m(\theta)$$$ describe a concave function, since $$$cos(x)$$$ for $$$-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}$$$ is concave. The sum of concave functions describe a concave function as well, so $$$p_m(\theta)$$$ must be a concave function. One nice property about concave functions is that the minimum value of the function is determined by the "edge" values for $$$\theta$$$, in our case by either $$$\theta_{min}$$$ or by $$$\theta_{max}$$$. This would mean that we can rotate the polygon by either $$$\theta_{min}$$$ or $$$\theta_{max}$$$ degrees to make the perimeter smaller. By that rotation, we manage to make one edge of the polygon intersect with the rectangle.
Now that we know that the minimum-perimeter rectangle has at least one of the sides collinear with the polygon, we can apply more or less the same algorithm as above, but instead of calculating the minimum total area we calculate the minimum total perimeter.
Merge two convex hulls
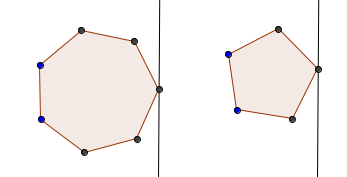
Merging two convex hulls into one convex hull can be done with a simple convex hull implementation. However, this is somewhat of an overkill, since we nearly don't have to do as many calculations with the rotating calipers technique as we would need to do with a regular convex hull implementation. To understand why using a convex hull algorithm would be an overkill here, let's take a look at an example:
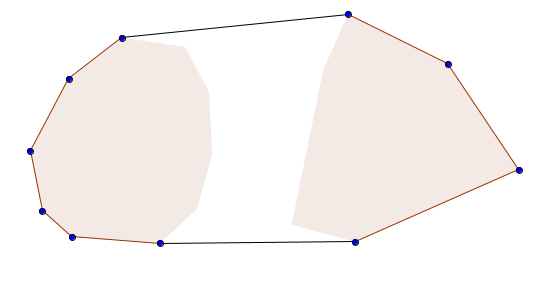
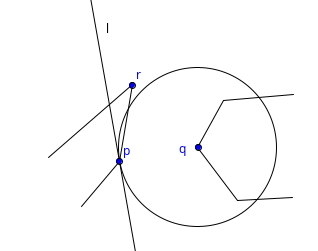
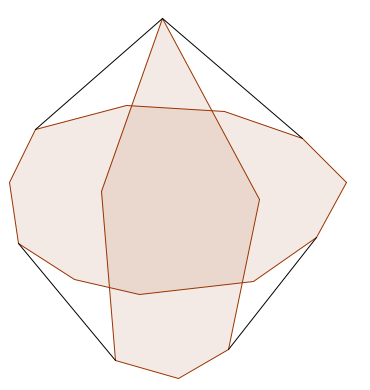
As we can see, to merge two convex hulls into one, we only need to find the two new edges that connect the two hulls and delete the vertices inside the interior. The edges that we need to find are called bridges. From the image above, we can see that the bridges, if extended, would form lines of support for both polygons $$$P$$$ and $$$Q$$$. So, in short, we need to find all lines of support that are lines of support for both polygons, and they must be lines of support in the same direction. A co-podal pair is a pair of vertices of $$$P$$$ and $$$Q$$$ that admit parallel lines of support in the same direction. So unlike with anti-podal pairs, which lay on opposite sides of the polygons, co-podal pairs must lay on the same side of the polygons respectively.
Consider a co-podal pair $$$p_i \in P$$$, $$$q_k \in Q$$$. The line $$$L = (p_i, q_k)$$$ is a bridge if and only if all vertices $$$p_{i-1}$$$, $$$p_{i+1}$$$, $$$q_{k-1}$$$ and $$$q_{k+1}$$$ lay on the same side of $$$L$$$. That holds true because if all of these vertices lay on the same side of $$$L$$$, then the line between $$$p_i$$$ and $$$q_k$$$ must be a line of support for both $$$P$$$ and $$$Q$$$. A simple algorithm description would be to generate all possible co-podal pairs and then check whether the 4 vertices mentioned above lay on the same side of the line between the co-podal pair. Note that this algorithm also works for intersecting polygons, a little bit of extra work has to be done however if one polygon is contained within the other. Also note that in certain cases, you need 4 bridges instead of two:
Critical support lines
Critical support (in short "CS") lines are lines of support of two polygons $$$P$$$ and $$$Q$$$ such that the polygons lay on opposite sides of the line. This line acts as a separating line between the two polygons. An image to visualize what we're trying to find here:
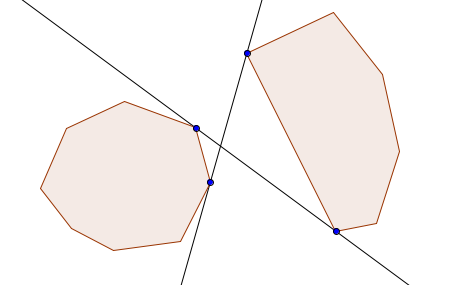
This problem is indeed very similar to the previous problem. Let $$$L = (p_i, q_k)$$$ with $$$p_i \in P, q_k \in Q$$$ be a CS line. The pair $$$(p_i, q_k)$$$ must be an anti-podal pair, since they admit the same line of support $$$L$$$, and they lay on opposite sides of the polygons. Also, the vertices $$$p_{i-1}$$$ and $$$p_{i+1}$$$ are not allowed to lay on the same side of $$$L$$$ as $$$q_{k-1}$$$ and $$$q_{k+1}$$$. Turns out, these two conditions are enough to determine whether a line is a CS-line or not.
Maximum width separating strip between two convex polygons
In this problem, we want to find the maximum width of a separating strip between two non-intersecting convex polygons $$$P$$$ and $$$Q$$$. A separating strip is defined by two parallel lines, one of which is a line of support for $$$P$$$, and the other is for $$$Q$$$. Between these two lines, there isn't allowed to be a vertex of neither $$$P$$$ nor $$$Q$$$:
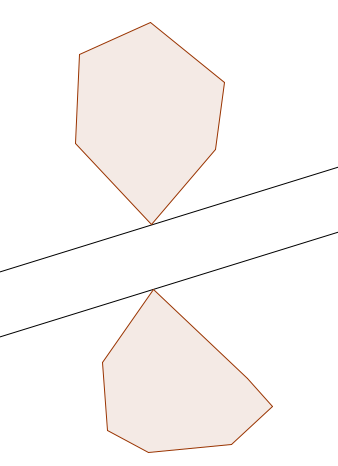
This is one example where we can use CS lines. If a vertex lays on the boundary of the separating strip, then it must be a vertex in between the two CS lines. Let the vertices $$$p_i \in P, q_k \in Q$$$ be the vertices that lay on the boundary of the separating strip. The pair $$$(p_i, q_k)$$$ must be an anti-podal pair. There are two possible cases that need to be considered:
- The line between $$$p_i$$$ and $$$q_k$$$ intersects one edge of either $$$P$$$ or $$$Q$$$. For that case, the rotating calipers algorithm is going to be used, iterating over every edge of $$$P$$$ and $$$Q$$$ and checking every anti-podal pair (a pair here denotes a pair of an edge and a vertex, not a pair of two vertices).
- The line between $$$p_i$$$ and $$$q_k$$$ doesn't intersect any edge. In that case, the width of the strip is going to be defined as the distance between the two vertices. However, we need an additional criterion to check whether such a pair even allows a strip with that width. Consider the line $$$L(p_i, q_k)$$$. A sufficient criterion would be if the angle between $$$L$$$ and each one of the edges $$$(p_{i-1}, p_i), (p_i, p_{i+1}), (q_{k-1}, q_k), (q_k, q_{k+1})$$$ to be greater that $$$90^{\circ}$$$.
Since there exist $$$O(n+m)$$$ anti-podal pairs for both cases, the total runtime of the algorithm would be, again, $$$O(n+m)$$$.
Minkowski sums of two convex polygons
In the last section of this blog, we will discover how to calculate the minkowski sums of two convex polygons using the rotating calipers technique. There exist other methods for achieving the same (such as sorting the edges by their polar angles) with the same time complexity, but this series wouldn't be complete without at least mentioning this application. So, what is the minkowski sum? The minkowski sum of two polygons $$$P$$$ and $$$Q$$$ is simply a new polygon that contains every possible sum of two points $$$p \in P$$$ and $$$q \in Q$$$. Formally, you can define the minkowski sum as:
while $$$p+q$$$ represents a vector addition. The first thing that we're going to look at is the fact that $$$P \oplus Q$$$ is a convex polygon as well. To see why this is true, we have to show that for every pair of points $$$pt_1, pt_2 \in P \oplus Q$$$, every point on the segment between $$$pt_1$$$ and $$$pt_2$$$ lays inside the minkowski sum as well. This segment can be described as:
Decompose $$$pt_1$$$ and $$$pt_2$$$ into their original vectors from $$$P$$$ and $$$Q$$$:
Now rewrite the line segment equation as:
The first summand must be a point between $$$p_1$$$ and $$$p_2$$$, and since $$$P$$$ is convex, it must lay inside $$$P$$$. Similarly, the second summand must lay inside $$$Q$$$. In total, this means that any point between $$$pt_1$$$ and $$$pt_2$$$ must lay inside the minkowski sum, therefore, the minkowski sum must be a convex polygon.
Now, what would you do if you wanted to construct the leftmost vertex of the minkowski sum? Since the $$$x$$$-value of the vertex would have to be minimum possible, it would only make sense to take the leftmost vertex of both $$$P$$$ and $$$Q$$$, since these vertices $$$x$$$-value is the smallest it could get. The same line of argument can be used if we want to compute the rightmost / highest / lowest vertex of the minkowski sum. Turns out, this argument can be generalized not for just only these 4 directions, but to all possible directions. So, if we want to have the diagonally left bottommost vertex of the sum, it only makes sense to take the diagonally left bottommost vertex of both polygons and sum them up etc. Such vertices are called extreme points for a specific direction. One nice property about these extreme points is that they form co-podal pairs. This holds true because parallel lines of support essentially have the same direction.
Since every vertex of the minkowski sum is also an extreme point for a specific direction, all vertices of that polygon must be sums of co-podal pairs of $$$P$$$ and $$$Q$$$. We can now use the rotating calipers algorithm to calculate the minkowski sum $$$P$$$ and $$$Q$$$.
The algorithm
First, we will calculate the point with the minimum $$$y$$$-coordinate and set that as our starting point. We then set up two horizontal lines that will act as parallel lines of support throughout this algorithm. This might look like this:
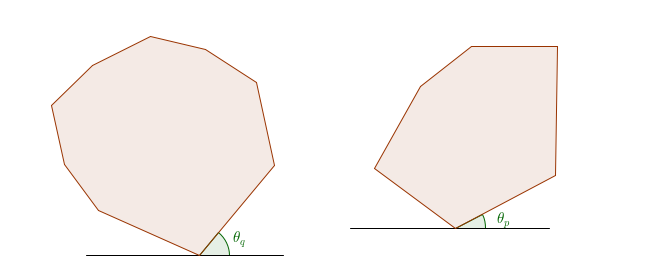
First, add the point with the minimum $$$y$$$-coordinate to our set of vertices. Then, while rotating around the polygon, we need to take care of a few cases. Assume that the sum $$$p_i + q_j$$$ was the last vertex that was added to the set of vertices:
- $$$\theta_p < \theta_q$$$: rotate by $$$\theta_p$$$ degrees and add $$$p_{i+1} + q_j$$$ to the set of vertices.
- $$$\theta_p > \theta_q$$$: rotate by $$$\theta_q$$$ degrees and add $$$p_i + q_{j+1}$$$ to the set of vertices.
- $$$\theta_p = \theta_q$$$: rotate by $$$\theta_p$$$ degrees and add $$$p_{i+1} + q_{j+1}$$$ to the set of vertices.
And that's it! The total runtime of this algorithm is $$$O(n+m)$$$, which is in fact optimal, since the minkowski sum has up to $$$n+m$$$ vertices.
Conclusion
Here, a few more applications of the paradigm were discussed. The huge number of problems that can be tackled using such a simple paradigm is the reason why I think that the rotating calipers is such an amazing algorithm. Hopefully, I was able to convince you of the same. If you have any questions about this blog, please let me know in the comments. There exist more applications of the algorithm, but I decided not to include them in this blog since they are too complex for a CP setting.