I'm the writer of this problem. Unfortunately, nobody submitted it during the contest.
Actually, the constraints have been weakened. My original constraints are max(1, m - 1000) ≤ n ≤ m and 1 ≤ t ≤ 109 due to I have an O((m - n)2) approach. rng_58 thought it's too complicated to solve it using an O((m - n)2) approach within the contest time. He found an O((m - n)3) approach that is quite different and easier to think of. ivan.metelsky gave an 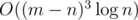 solution similar to rng_58's but needs less observations.
solution similar to rng_58's but needs less observations.
It's not hard to find that the answer is
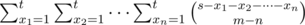
Because 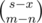 is a polynomial whose degree is m - n. Let
is a polynomial whose degree is m - n. Let

Then above summation can be rewrote to

Let 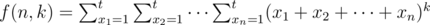 . It's not hard to find following recurrence relation:
. It's not hard to find following recurrence relation:
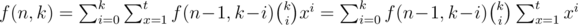
Due to n is very large, we have to use matrix multiplication to speed up it. Finally, we achieve an 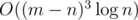 approach. bmerry's solution follows this idea and you can see it in arena.
approach. bmerry's solution follows this idea and you can see it in arena.
With a close observation with f(n, k)'s original form, it seems that there are at most n - m xi's power is greater than 0 after fully expanding (x1 + x2 + ... + xn)k.
So we do not need matrix, just choose some variables whose power is greater than 0 and only consider them. It optimizes previous approach to O((m - n)3). ftiasch's implementation in arena follows this idea.
I have posted my original idea in my personal blog. You can find it here.










