Hello, I'm the writer of SRM 655 Div1 Easy and Hard.

Div1 — Easy

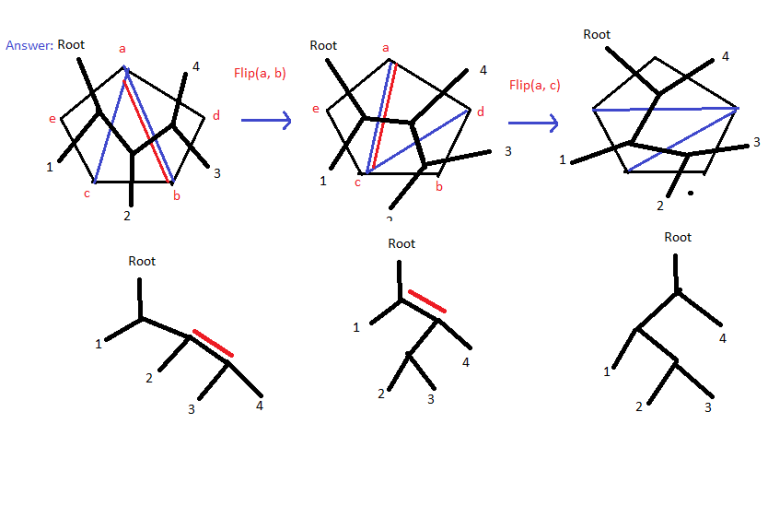
The key is to thinking from last operation: it will make the final board have a k by k monochrome rectangle.

for example, if we have:

BBBW
BWWW
BWWW
WWWW

Then we know in the last step we may paint the right-down 3 by 3 rectangle. And that means, before this step, these 3*3 cells can be any color. So the board will looks like:

BBBW
B???
B???
W???

And we can see the previous step could be upper-left 3 by 3 rectangle (because we can change '?' to 'B' and that is monochrome), so we get:

???W
????
????
W???

And we are done, because if we change '?' to 'W' that is all-white board.

So the algorithm is: keep finding k by k monochrome rectangles and paint it into '?', until can't do it. And check if the board is all-white. You can proof no matter the order of rectangle we choose to paint, we will get the same result.

Code: http://ideone.com/xM13nh

Fun fact: I come up with this idea when I was playing a mobile game: Strata. Usually puzzle games are NP-Hard, but I find this one is not. :P

Div1- Hard

First let's think about how can I solve it if we change blue points to a circle:

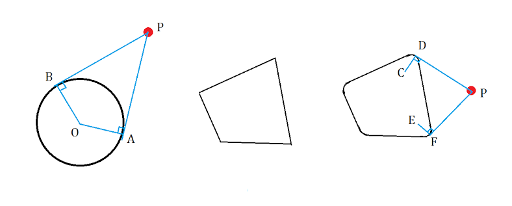
(If you can't see the picture, please use this url: http://postimg.org/image/ssvbih7sd/)

For a point P, we say it covers the direction [OA, OB] of that circle.

We can prove: "circle totally in the CH of points" if and only if the union of directions of each point covers is all 360 degree.

The polygon version is same. We can change the vertex to an infinite small arc of circle. Then P will cover the direction [EF, CD]. The condition will remain same.

So the problem becomes: we have lots of interval of directions, each one have a certain probability of occur, you are ask the probability that the union will be [-Pi, Pi]. That could be solved by DP (my solution is N^3).

Code: http://ideone.com/Yq4ReK

Fun fact: there is a simplified version (2 blue points instead of up to 100, but require n^2 solution) used in TCO 2012 round 3B Hard wrote by ivan.metelsky, but today he was solving this harder version during the contest!

And congratulations to tourist! He solved all 3 tasks with highest score with 7 successful challenge!

Hello, I'm the writer of SRM 651.

It turns out this round is unrated due to some system failure. Sorry about the inconvenience it caused. I hope Topcoder can improve their infrastructure soon so that can be as good as codeforces.

I will post the problem statement, reference solution and a short editorial here.

Welcome to discuss the tasks, as well as to give feedback about them!

Problem Statement: http://www.speedyshare.com/2kRaC/task.rar

Reference solution:

Div1-Easy: http://ideone.com/a9siv1

Div1-Medium: http://ideone.com/sbEZSH

Div1-Hard: http://ideone.com/9JXoSL

Div1-Easy: RobotOnMoon

Look at this example:

....
.S.#
....

There will be infinite long perfect safe sequence, why? because we have "RRR...". That means if there is one '#' at any of the 4 direction of 'S', then the answer will be -1..

Then look at this example:

#.##
.S..
#.##
#.##

since there is only 1 cell to the left of 'S', there can be at most 1 'L' in any perfect safe sequence, otherwise if all characters other than 'L' are missing, it will lead the robot to die. So we can have a maximal bound of length of any perfect safe sequence: we have at most 1 'L', at most 2 'R', at most 1 'U' and at most 2 'D'. And we could find "LRRUDD" is perfectly safe: we have only 1 'L' so it is impossible to move outside the board from the left edge, etc.

So if the answer is not -1, then it must be n+m-2.

Div1-Medium: FoxConnection3

The key is notice that there can be few "shapes" of the result connected foxes. In fact if n = 6 there can be at most 216 of them: http://oeis.org/A001168

And then we should figure out which fox goes to which position in the final shape. There will be 6! ways.

Then we need to decide the position of our final shape.

After decide the position, we will calculate how many steps do we need to get it. It is simply the sum of length of shortest paths from s[i] to t[i] where s[i] is the start position of fox[i] and t[i] is the end position of fox[i], because we can ignore "there cannot be two foxes in the same cell at the same time." by this way:

Suppose we want to move O to x in this situation:

.O..o...o.x.

There are 2 foxes block our way, but we can do this:

.o..o...o.x. -> .o..o.....o. -> .o......o.o. -> ....o...o.o.

The if we write down the equation, it will be something like abs(offsetX — u[0]) + ... + abs(offsetX — u[n-1]) + abs(offsetY — v[0]) + ... + abs(offsetY — v[n-1]). We can find we should set offsetX = middle number of u[] and offsetY = middle number of v[].

Div1-Hard: FoxAndSouvenir

It will be quite easy to get a solution run in O(n^4) for each query, a classic DP:

dp[i] = how may ways to get exactly i dollar.

initially we have dp[i] = {1, 0, 0, ...}

For each souvenir of price p, we update new_dp[i] = dp[i] + (i-p>=0 ? dp[i-p] : 0).

So how to improve this? One observation is that this kind of dp can be write into convolutions:

for example, new_dp[i] = dp[i] x {1, 0, 0, ..., 1, 0, .., 0}.

Then one possible improvement is FFT with 2D segment tree, but it will need O(n^4 (logn)^4) which is too slow.

Another observation is that, we shouldn't do lots of FFT to merge segments again and again, for example, the answer will be {1, 0, .. , 1, 0, ..} x {1, 0, .. , 1, 0, ..} x {1, 0, .. , 1, 0, ..} ... We should first transform all of them into frequence domain, do the pointwise product of all of them. then transform back the result into time domain.

The last observation is it: we can transform {1, 0, .. , 1, 0, ..} into frequence domain in O(n) by bruteforce instead of O(n logn) by FFT, because we only have 2 non-zero values. And we just need one point value in time domain, so we can get it by brutefoce in O(n) instead of paying O(n logn) to reconver all elements in time domain.

So the solution looks like: preprocoss s[i][j][k] — the pointwise product of index k in frequence domain of the subrectangle [0, 0] — [i, j]. Then for one query we can find the frequence domain value of index k by calculate s[xMax][yMax][k] * s[xMin-1][yMax][k]^(-1) * s[xMax][yMin-1][k]^(-1) * s[xMin-1][yMin-1][k].

We should do the DFT over GF(1000000009). And we can avoid 0s in s[i][j][k] by use a length of an odd number. There are lots of divisors of 1000000008, we can choose 3507, the smallest odd divisor that is no less than 2500.

Update 1 : here are the reference solutions for this contest:

1. Div2-A: http://ideone.com/JP1Ksj
2. DIv2-B: http://ideone.com/udz3bN
3. Div2-C / Div1-A: http://ideone.com/KVobNb
4. Div2-D / Div1-B: http://ideone.com/7MQqOm
5. Div2-E / Div1-C: http://ideone.com/z3FsU2
6. Div1-D: http://ideone.com/Y7j21a
7. Div1-E: http://ideone.com/Orbacp

Note that for Div2-E / Div1-C, it is for the harder version: we need to handle '1' in the cycle.

510A - Fox And Snake

There are 2 different ways to solve this kind of task:

First one is to simulate the movement of the snake head, and you draw '#'s on the board. The code will look like:

head = (1, 1)
repeat:
	repeat m-1 times: head move to right
	repeat 2 times: head move down
	repeat 2 times: head move down
	repeat m-1 times: head move to left
	repeat 2 times: head move down
	repeat 2 times: head move down
until head is out of the board

Another way is to do some observation about the result, you can find this pattern:

(4k+1) / (4k+3) line: "#######"
(4k+2) line: ".......#"
(4k+0) line: "#......."

510B - Fox And Two Dots

This task is essentially ask if there is a cycle in an undirected graph: treat each cell as a node, and add an edge if two cells are neighborhood and have some color.

There are lots of ways to do this, for example:

1. Run dfs / bfs, if an edge lead you to a visited node, then there must be a cycle.

2. For each connected component, test if |#edges| = |#nodes| - 1, if not then there must be a cycle.

510C - Fox And Names / 512A - Fox And Names

Let's first think about what S < T can tell us: suppose S = abcxyz and T = abcuv. Then we know that S < T if and only if x < u by the definition.

So we can transform the conditions name₁ < name₂, name₂ < name₃ ... into the order of letters.

Then the question become: do we have a permutation that satisfy those conditions. It is actually the classic topological order question.

One trick in this task is that, if we have something like xy < x then there is no solution. This is not covered in pretests. :)

510D - Fox And Jumping / 512B - Fox And Jumping

This task equals to: what is the minimal sum of costs that we can select k cards, so their GCD is 1.

First observation is that: GCD(x₁, x₂, ..., x_k) = 1 means that for any prime p, there exist i such that x_i is not dividable by p. So we only care about what prime factors a number contain. (So for example, 12 -> {2, 3}, 6 -> {2, 3}, 9 -> {3]})

The second observation is: If x ≤ 10⁹ then it has at most 9 prime factors.

So after we select one number, we only care about these 9 or less primes. Then this problem equals to set covering problem (SCP), it can be done by mask DP. It can run in about O(2^9 * n^2).

510E - Fox And Dinner / 512C - Fox And Dinner

First finding is: if a + b is a prime, then one of them is an odd number, another is an even number. (that's why we set 2 ≤ x_i)

Then we could find: every odd number have exactly 2 even number as neighborhood, and every even number have exactly 2 odd number as neighborhood. And that means we need |#even| = |#odd| to have a solution.

So it looks like bipartite graph matching, but every element matched 2 elements. And in fact it can be handled by maxflow: For each odd number, we add a node on the left side and link it from source with capacity equals to 2, and for each even number, we add a node on the right side and link it to sink with capacity equals to 2. And if sum of two numbers is a prime number, we link them with capacity equals to 1.

Then we solve the max flow, it have solution if and only if maxflow = 2 * |#even|.

We can construct the answer(cycles) from the matches.

Note: Actually this task is still solvable if we allow a_i = 1. But you need some clever way to deal with it. We think it is too hard so we removed this case. What do you think about this decision?

512D - Fox And Travelling

We could find that some nodes cannot be visited. And more specific, if one node is in a cycle then it cannot be visited. So what about the structure of nodes that we can visit?

Let's first find a way to get all nodes that could be visited. We can deal with this by something like biconnected decomposition, but that is not easy to implement. In fact we can use this simple method: each time we pick one node that have at most 1 neighborhood and delete it. Repeat this process until we can't do it anymore.

We could find these nodes are actually belonging to these 2 kinds: 1. A tree. 2. Rooted tree. (that means, the root is attached to a cycle)

The rooted tree case is simple: we can solve it by tree DP. The state will be dp[i][j] = the way to remove j nodes in the subtree rooted at i.

Then how to solve the unrooted tree case? The way to deal with that is to transform it into rooted case. We have 2 solution:

1. We select one unvisited node as the root by some rules: for example, we select one with minimal index. Then we just need to modify the DP a bit to adjust this additional condition.

2. We could find if the tree has n nodes and we visit k nodes in the end, then there will be max(1, n-k) ways to choose the root. That means if we choose every node as the root and sum up them, we will count this case exactly max(1, n-k) times. So we just do the rooted DP for from node n times, and divide max(1, n-k) for ans[k].

The overall complicity is O(n⁴), and it can be optimize into O(n³) if you like.

512E - Fox And Polygon

Triangulation of polygon is something hard to think about. So the first key observation is that, we can transform this task into operations on rooted trees!

One Triangulation of polygon can be mapping to one rooted tree. And the flip operation can be mapping to the rotation of trees. (It is the operation we used to balance our BST) You can find the mapping from above picture. The red lines indicate the edge that will be flipped and the nodes we rotated.

Then we should find a standard shape of the tree, and solve this task: how to rotate any tree into this standard shape?

My solution is to choose the balanced tree as standard shape. The way to do that is this: find the node that the index is the middle number, rotate it to the top(that what we did for splay tree), and do the same thing for each subtree.

It is easy to see it could work in O(nlogn) steps.

Лиса Ciel возвращается!

Все приглашаются поучаствовать в Codeforces Round #290, который начинается в обычное время в ближайший понедельник.

Это мой четвёртый раунд на Codeforces, можете ознакомиться с моими предыдущими раундами: #190, #228, #270.

Последний Div1-раунд (#286) оказался очень непростым, поэтому мы решили уменьшить сложность раунда (например, Div1-E превратилась в Div1-D). Надеюсь, это позволит большому количеству людей насладиться всеми задачами раунда: в этот раз ни одна задача не требует продвинутых знаний наподобие линейной алгебры или преобразования Фурье.

Главным персонажем раунда будет Лиса Ciel и её жизнь: она учится программировать, играет, путешествует, принимает ужин, а также делает многое другое.

Как и на раунде #228, топ-20 участников, присутствующих на зимних сборах в Петрозаводске, будут награждены футболочками Codeforces. Футболку может получить любой участник сборов, член жюри, тренер, организатор или любой другой человек, так или иначе присутствующий на сборах.

Как обычно, спасибо Zlobober за ценные советы и помощь в подготовке моего раунда, и MikeMirzayanov за платформы Codeforces и Polygon.

Удачи!

Update1: Score Distribution is ... Div2: Standard (500 — 1000 — 1500 — 2000 — 2500), Div1: a bit unusual ... (500 — 1000 — 1500 — 2250 — 2250)

Update2: Editorial: http://mirror.codeforces.com/blog/entry/16173

Update3: Congratulation to our winners:

Div1:

1. Petr

2. Endagorion

3. mmaxio

4. jqdai0815

5. tourist

They are all people who solved 5 tasks!

Div2:

1. SkullSkin

2. joshkirstein

3. gabrielinelus

4. UnknownNooby

5. Andrey_WK

472A - Уроки дизайна задач: учимся у математики

One way to solve this is by bruteforce: there are O(n) different ways to decomose n as sum of two number. If we can check if a number is a prime in O(1) then the whole algorithm can run in O(n). You can use Sieve of Eratosthenes to do the pre-calculation.

And another way is try to prove this theorem. The prove is simple: if n is odd number, then 9 and (n-9) is an answer (n-9 is an even number at least 4, so a composite number), and if n is even number, then 8 and (n-8) is an answer (n-8 is an even number at least 4, also must be a composite number).

472B - Уроки дизайна задач: учимся у жизни

This task can be solve by greedy: the k people with highest floor goes together, and next k people with highest floor goes together and so on. So the answer is 2 * ((f[n]-1) + (f[n-k]-1) + (f[n-2k]-1) + ...) .

It is a bit tricky to prove the correctness of greedy, since people can get off the elevator and take it again. We can give a lower bound of the answer by flow analysis: between floor i and floor i+1, there must be no more than (# of f[i] >= i+1) / k times the elevator goes up between these 2 floors, and then there be same number of times goes down. We can find this lower bound matches the answer by above greedy algorithm, so it means the greedy algorithm gives an optimal answer.

472C - Уроки дизайна задач: недетеминированность

This one laso can be solved by greedy, let's think in this way: let pick one with smallest handle, then we let him/her use min(firstName, secondName) as handle. And go for the next one (2nd mallest handle), now he/she must choose a handle greater than handle of previous person, and if both meet this requirement, he/she can pick a small one.

This time the correctness of this greedy solution can be proved by exchange argument.

Note that if we change the goal of this problem: ask number of different permutations they can get, then it will be very hard. (I tried it for hours but can't solve.)

472D - Уроки дизайна задач: обратные задачи

Let's think it in the following way: for the minimal length edge, it must belong the the tree, ..., for the k-th minimal length edge(a, b), if there is already an path between a-b, then it can not be an edge of tree anymore, otherwise it must be edge of tree, why? Because otherwise there must be a path from a to b in the tree, that means a and b can be connected by edges with less length, but a and b is not connected.

So this Kruskal style analysis gives us this theorem: if there is an answer, then the answer must be the MST of that graph. (You can also guess this theorem and try to prove it.)

You can solve MST in O(n^2 log n), and then there are many way to check distance between notes on tree: you can just simply do dfs or bfs from each node, it can run in O(n^2). Or if you have pre-coded LCA algorithm, it can run in O(n^2 log n).

472E - Уроки дизайна задач: учимся у игр

First let's solve some special cases:

If the initial board and the target board contains different orbs, then there can't be a solution.

If n = 1 (or m = 1), then we can try all O(m^2) (or O(n^2)) possible moves.

And for the other cases, there always have solution. We first hold the orb with number target[1][1] in initial board. Then we want to move other orbs to their position.

So let's come up with a process to move orb from (a, b) to (c, d): it must be some continue path from (a, b) to (c, d), so we want to build a single move: it will move an orb from (a, b) to an adjacent cell (c, d). How to do that? We can move our touching orb to (c, d) first, and then move to (a, b). But there are some concerns: in this move, the touching orb shouldn't pass any already-done cells, and it shouldn't pass (a, b) when we get to (c, d).

That means we need a good order to move orbs. We can do it in this way: first, as long as there are more than 2 rows, we move the orbs to last row (from left to right or right to left). And then it must be 2xm boards: we do it column by column from right to left. We can find that in this order, there always exist paths for our touching orb to get (c, d).

472F - Уроки дизайна задач: меняем цель задачи

You need to know some knowledge about linear algebra and notice the operation of xor on 32 bit integers equals to + operation in a 32 dimension linear space. If you don't know, you should learn it from the editorial of similar tasks, for example, Topcoder SRM 557 Div1-Hard.

We need to know some basic properties of our operation:

1. we can swap two number a and b by: a^=b, b^=a, a^=b.

2. This operation is inversible, the inverse is itself.

By property 1 we can do the Gaussian elimination of each set of vectors.

By property 2 we can use this way to build an answer: use some operation to make A[] into a base (linear independent vectors that the span will be A[]), then transfer it into a base of B[], then use the inverse of Gaussian elimination to recover B[].

So now we have two bases: {a1, a2, ..., ax} and {b1, b2, ..., by}. If there exists some bi such that it can't be expressed as a linear combination of {a1, a2, ..., ax}, the solution can't exists.

Otherwise there always exists a solution: first we build b1 and put it in the first position. Suppose b1 = a2 ^ a3 ^ a8, then we swap any of them, say, a2 into position one, and then xor it with a3 and a8, then we get b1. Note that after this operation {a1, a2, ..., ax} will remain a base. And we need to ensure we don't erase already-done numbers in a.

472G - Уроки дизайна задач: увеличиваем ограничения

Let's start with a simpler task: we have string A and B (|A|, |B| <= n), we have q queries and each query we ask the Hamming distance between A and a substring of B with length equals to |A|.

How to solve this? We need to notice compute A with different offset of B is similar to the computation of convolution, so it can be done by FFT.

We use +1 to replace '1' and we use -1 to replace '0', and then we do the convolution of A and reverse B. We can extract the answer of all possible query of "the Hamming distance between A and a substring of B with length equals to |A|."!

Then let's come back to our problem, how to use this way to make a faster solution? We can use a way like sqrt decompose: we divide A into L blocks, for each block, we compute the convolution of this part with B, it will takes O(n*L*logn). And for each query, we can use the pre-calculated results to speedup (if a whole block contains in the query, we can compute it in O(1)). So each query needs no more than O(L) operation.

If n = q then this solution can run in O((n*logn) ^ 1.5). But in practice it has some issues: for example, we can use bit operation to speedup like __builtin_popcount(). I tried to set constraints to fail solution with only bit optimization, but seems I failed: I apologies to allow this kind of solutions passed. (I used __builtin_popcount() to test such solution, but in fact cnt[x<<16] + cnt[x>>16] is much faster than the builtin fucnion)

(Also, you can use your knowledge about real world computers to solve this task: http://mirror.codeforces.com/contest/472/submission/8014415)

Хотите выиграть футболу? Или узнать как придумывать задачи для соревнований по программированию? А как насчет порешать 7 задач за два с половиной часа?

Если ответ хотя бы на один вопрос из перечисленных выше -- да, тогда Codeforces Round #270 непременно для вас. Раунд был разработан мной в Калифорнии, и приготовлен в системе Polygon (оригинал: designed by me in California, assembled in polygon). Спасибо MikeMirzayanov за прекрасную систему и Gerald за помощь в организации и тестирование раунда. Раунд стартует в обычное время в воскресенье, не упустите возможность посоревноваться!

Организаторы Marathon24 решили сделать подарок лучшим участникам раунда! Лучшие 25 участников получат специальные футболки от Marathon24! Большое им спасибо!

Эта картинка всего лишь для привлечения вашего внимание. Настоящие футболки будут иметь специальный дизайн от Marathon24!

Существует несколько статей, которые призваны научить, как стать автором задач для соревнований по программированию. Например, Problemsetter's Memoir и Way of Problemsetter. Но все они детально рассматривают только лишь процесс подготовки задач. Возможно, вы не знаете как начать готовить контесты по той причине, что у вас нет идей для задач.

В последние три года я подготовил очень много задач. Например, два Codeforces раунда (#190 и #228), также я подготовил ровно 100 задач для Topcoder. Поэтому я решил написать небольшой учебник, чтобы поделиться своими знаниями по придумыванию задач с общественностью... Стоп, как насчет привести контест, в условиях задач которого будут содержаться советы по придумыванию задач. Так я пришел к идее: в каждой задаче контеста будет описываться определенный способ придумать новую задачу, затем в качестве примера в условии будет описан процесс придумывания новой задачи этим способом; эту новую задачу вам и предстоит решить!

Обратите внимание, этот раунд будет немного специфическим: все участники (и Div1, и Div2) будут соревноваться в одном и том же контесте, а контест будет состоять из 7 задач! Продолжительность контеста увеличена до двух с половиной часов.

В конце я хочу немного рассказать о себе (как это сделал marat.snowbear в предыдущем анонсе). Меня зовут Gaoyuan Chen, и родом я из Китая. Я жил в Beijing в течение 23 лет (до этого августа), а затем поступил в университет южной Калифорнии в Лос Анджелесе, чтобы научиться разработке игр. Как разработчик игр я постарался сделать раунд как можно более интересным (конечно, в раунде есть задача про известную игру). Когда я переехал в штаты, я стал использовать Facebook, так что если вы хотите узнать меня лучше или пообщаться со мной в чате, заходите на мою страницу: https://www.facebook.com/cgy4ever.

Остальная информация, например, разбалловка задач (возможно, последняя задача будет иметь стоимость 3500!) будет опубликована позднее.

Желаю всем удачи и удовольствия от решения задач!

Update1 : Разбалловка: 500 — 1000 — 1500 — 2000 — 3000 — 3000 — 3500

You can find the editorial and my solutions here: https://github.com/cgy4ever/CF228

389A - Лиса и игра с числами

First we know that: in the optimal solution, all number will be equal: otherwise we can pick a and b (a < b) then do b = b — a, it will make the answer better.

Then we need an observation: after each operation, the GCD (Greatest common divisor) of all number will remain same. It can be proved by this lemma: if g is a divisor of all number of x[], then after the operation, g is still the divisor of these numbers, and vice versa.

So in the end, all number will become the GCD of x[].

Another solution that can pass is: While there exist x[i] > x[j], then do x[i] -= x[j]. We can select arbitrary i and j if there exist more than 1 choice.

389B - Лиса и крест

Let's define the first # of a shape is the cell contain # that have the lexicographical smallest coordinate. Then the first # of a cross is the top one.

Then let x be the first # of the given board. (If the board is empty, then we can draw it with zero crosses.) x must be covered by a cross, and x must be the first # of the cross. (You can try 4 other positions, it will cause a lexicographical smaller # in the board than x)

So we try to cover this x use one cross, if it leads some part of the cross covers a '.', then there will be no solution. If not, we just reduce the number of # in the board by 4, we can do this again and again.

389C - Лиса и коробки / 388A - Лиса и коробки

We need some observation:

1. There exists an optimal solution such that: in any pile, the box on the higher position will have a smaller strength.

2. Let k be the minimal number of piles, then there exists an optimal solution such that: The height of all piles is n/k or n/k+1 (if n%k=0, then all of them have the height n/k).

We can prove them by exchange argument: from an optimal solution, swap the boxes in it to make above property holds, and we can ensure it will remain valid while swapping.

Then for a given k, we can check whether there exist a solution: the i-th (indexed from 0) smallest strength needs to be at least i/k.

So we can do binary search (or just enumerate, since n is only 100) on k.

389D - Лиса и минимальный путь / 388B - Лиса и минимальный путь

First we need to know how to calculate the number of different shortest paths from vertex 1 to vertex 2: it can be done by dp: dp[1] = 1, dp[v] = sum{dp[t] | dist(1,t) = dist(1,v) — 1}, then dp[2] is our answer.

We need to do dp layer by layer. (first we consider vertexes have distance 1 to node 1, then vertexes have distance 2 to node 1 and so on.) So we can construct the graph layer by layer, and link edges to control the dp value of it.

My solution is construct the answer by binary express: If k is 19, then we need some vertexes in previous layer such that the dp value is 16, 2 and 1. So we just need a way to construct layer with dp value equals to 2^k.

In the first layer, it contains one node: 1, it has the dp value 1. In the next layer, we can construct 2 nodes, with dp value equals to 1. (We use [1 1] to denote it). And the next layer is [1 1 2], then [1 1 2 4], [1 1 2 4 8] and so on. So we need about 30 layers such that gets all 2^k where k < 30. It uses about 500 nodes.

389E - Лиса и игра в карты / 388C - Лиса и игра в карты

First let's consider the case which all piles have even size. In this case, we can prove: in the optimal play, Ciel will gets all top most half cards of each pile, and Jiro gets the remain cards.

We can prove by these facts: Ciel have a strategy to ensure she can get this outcome and Jiro also have a strategy to ensure this outcome. (For Jiro this strategy is easy: just pick the card from pile that Ciel have just picked. For Ciel it's a little bit harder.)

Why we can conclude they are both the optimal strategy? Ciel just can't win more, because if she played with Jiro with above strategy, Jiro will get the bottom half of each pile.

Then we come back with cases that contain odd size piles. The result is: for odd size pile, Ciel will get the top (s-1)/2 cards and Jiro will get the bottom (s-1)/2 cards. Then what about the middle one? Let's denote S is all such middle cards. Then we define a reduced game: In each turn, they pick one card from S. The optimal play for this game is easy: Ciel gets the max one, and Jiro gets the 2nd largest one, and Ciel gets the 3rd largest one and so on.

We can prove Ciel have a strategy to get: all top half parts + cards she will get in the optimal play in the reduced game. And Jiro also have a strategy to get: all bottom half parts + cards he will get in the optimal play in the reduced game. And these strategy are optimal.

388D - Лиса и идеальные наборы

A perfect set correspond to a linear space, so we can use base to represent it. We do the Gauss–Jordan elimination of vectors in that set, and can get an unique base. (Note that we need to to the all process of Gauss–Jordan elimination, including the elimination after it reached upper triangular)

And we can construct the bases bit by bit from higher bit to lower, for a bit:

1. We can add a vector to the base such that the bit is the highest bit of that vector. And at this time, all other vector will have 0 in this bit.

2. Otherwise we need to assign this bit of each vector already in the base. If now we have k vector, then we have 2^k choices.

And when we do this, we need to know what's the maximal vector in this space. It's not hard:

1. If we add a vector, then in the maximal vector, this bit will be 1.

2. Otherwise, if we don't have any vector in base yet, then this bit will be 0. Otherwise there will be 2^(k-1) choices results in this bit of maximal vector will be 0, and 2^(k-1) choices results in 1.

So we can solve this task by DP bit by bit.

388E - Лиса и метеоритный дождь

All tasks beside this are very easy to code. And this one focus on implementation.

We can represent the orbit of each meteor by a line in 3D space. (we use an axis to represent the time, and two axis to represent the position on the plane.)

Then the problem becomes: we have some lines in 3D space (they are not complete coincide), find a largest clique such that each pair of lines touch at some point.

We need this observation: If there are 3 lines in the optimal clique, and these 3 lines are not share a common point, then all line in this clique will on a plane.

By using this observation, we only need to consider 2 cases:

1. All lines in the clique have a common point.

2. All lines in the clique are on the same plane.

Both are easy tasks in theory, but it needs some coding.

There are two ways:

1. Use integer anywhere. Note that the coordinates of intersection can be rational number, but can't be irrational, so we could do this. We can use some way to encode the plane, direction.

2. Use floating number. To count same number of points, we can sort (x, y, z) by using the following compare function: if (abs(A.x — B.x) > eps){return A.x < B.x} otherwise { if(abs(A.y-B.y)>eps){return A.y < B.y} otherwise return A.z < B.z}.

Привет всем!

В понедельник третьего февраля 2014 года в 19:30 по московскому времени состоится Codeforces Round #228 (Div1 + Div2).

Этой мой второй раунд на Codeforces (кликните сюда, чтобы посмотреть предыдущий). Как обычно, в раунде будет семь задач: две — только для Div2, две — только для Div1 и три общие задачи. Точно так же, как и в прошлый раз, главным героем задач раунда будет лиса Ciel.

Благодарю Gerald за тестирование задач и MikeMirzayanov за проект Codeforces и систему Polygon.

Желаю удачи и фана от решения задач!

Распределение баллов будет анонсировано позже. А разбор задач будет опубликован сразу после системного тестирования.

Кроме всего прочего, вчера в Китае отмечали новый год. Поздравляю всех, кто отмечал этот праздник! И, конечно, я очень рад, что именно я автор первого контеста в новом году.

Update1: Приятная новость для участников Петрозаводских сборов. Top 20 участников сборов по итогам этого раунда, которые придут на закрытие, получат футболки от Codeforces.

Update 2: Распределение баллов по задачам стандартное. (500-1000-1500-2000-2500).

Update 3: Приносим извинения, раунд перенесен на 10 минут по техническим причинам.

Update 4: Продолжительность соревнования увеличена на 5 минут.

Update 5: Contest ended, thanks for your participating! I'll post the editorial soon.

Update 6: разбор.

Победители:

DIV1:

1. tourist
2. PavelKunyavskiy
3. Egor
4. 2222
5. dreamoon_love_AA

К сожалению, никто не решил задачу Е. Решение Egor-a могло пройти тестирование, если бы TL был бы равен 7 секундам, вместо 6. Какая жалость!

DIV2:

1. I_love_Hoang_Yen
2. iaacboy
3. GoldExperience
4. shivatejesh
5. lordpawel

Только они решили все предложенные задачи!

Update 1 Added links to my code.

Update 2 The links to my code seems not work, so I push my codes on github, and you find all of them here: https://github.com/cgy4ever/cf190

Update 3 Fixed my solution of Div1-C (Div2-E). In this problem, we must find centroid of tree instead of center of tree. Thanks RomaWhite for pointing this out and provide test case. And it seems that many solutions can pass the system test will fail on his test case (including my model solution). I feel apologetic for the weak test cases and wrong solution.

Update 4 Reformat the passage, I hope it would looks better.

322A - Ciel and Dancing

Let's define remainNew = # of people haven't danced before. So at beginning remainNew = n+m, and we have:

• During the 1st song, remainNew must decreased by at least 2. (Because the boy and girl must haven't danced before.)
• During the k-th (k>1) song, remainNew must decreased by at least 1. (Because one of the boy or girl must haven't danced before.) So the answer must be no more than n+m-1.

And it's not hard to construct one schedule get this maximal possible answer:

1 1
1 2
...
1 m
2 1
3 1
...
n 1

322B - Ciel and Flowers

If there are no "mixing bouquet" then the answer will be r/3 + g/3 + b/3. One important observation is that: There always exist an optimal solution with less than 3 mixing bouquet.

The proof is here: Once we get 3 mixing bouquet, we can change it to (1 red bouquet + 1 green bouquet + 1 blue bouquet)

So we can try 0, 1, 2 mixing bouquet and make the remain 3 kind of bouquets use above greedy method. Output one with largest outcome.

322C - Ciel and Robot 321A - Ciel and Robot

Note that after Ciel execute string s, it will moves (dx, dy). And for each repeat, it will alway moves (dx, dy). So the total movement will be k * (dx, dy) + (dx[p], dy[p]) which (dx[p], dy[p]) denotes the movement after execute first p characters. We can enumerate p since (0 <= p < |s| <= 100), and check if there are such k exists.

Note that there are some tricks:

• We can divide dx or dy directly because they both can become zero.
• Another trick is that k must be non-negative.

Many people failed on this test case (which no included in the pretest):

-1 -1
UR

322D - Ciel and Duel 321B - Ciel and Duel

We have 3 solutions to this problem:

= 1. greedy =

There are 2 cases: we killed all Jiro's cards, or not.

If we are not killed all of Jiro's cards, then:

1. 1. We never attack his DEF cards, it's meaningless.
2. Suppose we make k attacks, then it must be: use Ciel's k cards with highest strength to attack Jiro's k cards with lowest strength, and we can sort the both k cards by strength to make attack one by one. (If there are an invalid attack, then we can't have k attack)

If we kill all Jiro's card: Then for all DEF cards, we consider it from lower strength to higher: if its strength is L, then we find a card of Ciel with strength more than L (If there are many, we choose one with lowest strength). Then we can know if we can kill all DEF cards. And then we choose |x| cards with highest strength of Ciel, try to kill Jiro's remain card.

Note that if we could kill all ATK cards, the order doesn't matter: the total damage will be (sum of strength of Ciel's remain card) — (sum of strength of Jiro's remain card).

= 2. DP =

Above solution looks complicated, can we solve it with few observation? Yes we can. The only observation is that:

There always exist an optimal solution that: If Ciel's two card X's strength > Y's strength, and X, Y attacks on A and B with the same position, then A's strength > B's strength. We already use this observation in above solution.

Then what can we do? Yes, we can sort all Ciel's card, all ATK card of Jiro, all DEF card of Jiro.

Let's DP[pCiel][pATK][pJiro][killAll] be the state that next unconsidered card of Ciel, Jiro's ATk, Jiro's DEF are pCiel, pATK, pJiro, and killAll=1 if and only if we assume at the end we can kill all Jiro's card.

Then we have 4 choice:

1. Skip, this card don't attack.
2. Attack on the next ATK card.
3. Attack on the next DEF card.
4. Assume Jiro has no cards and make a direct attack.

= 3. MinCostMaxFlow =

Well, what if we want to solve this problem with no observation?

Ok, if you are good at construct flow algorithm, it's an easy thing to solve this by flow.

Please see my solution for details. It just considered the matching relationship.

322E - Ciel the Commander 321C - Ciel the Commander

This is a problem with construction on trees. And for these kind of problems, we usually use two method: up-down or down-up. So we have 1 solution for each method:

= 1. up-down construction =

Suppose we assign an officer with rank A at node x. Then for two distinct subtree rooted by x, says T1 and T2: There can't be any invalid path cross T1 and T2, because it is blocked by node x. (It's clear that we can't make 2 rank A officer.)

So we can solve these subtree independently: the only different is that we can't use rank A anymore.

Then the question is: which node should x be? It could be good if any subtree will has a small size. And if you have the knowledge of "centroid of tree", then you can quickly find that if x be the centroid of this tree, the subtree's size will be no more than half of the original tree. So we only needs about log2(n) nodes and 26 is enough.

= 2. down-up construction =

The above solution involves the concept of "centroid of tree" but you might not heard about that, don't worry, we have another solution can solve this problem without knowing that, and it's easier to implement.

Suppose we choose 1 as the root and consider it as a directed tree, and on some day we have the following problem:

We have some subtree rooted at T1, T2, ..., Tk, and they are already assigned an officer, we need to assign an officer to node x and link them to this node. Well, a normal idea is: we choose one with lowest possible rank.

The rank of x should satisfy:

1. If there are a node with rank t exposes at Ti and a node with t exposes at Tj (i!=j), then rank of x must be higher than t. (Otherwise the path between them will be invalid.)
2. If there are a node with rank t exposes at Ti, then the rank of x can't be t.

So we can use this rule to choose the lowest possible rank. But can it passes? Yes, it can, but the proof is not such easy, I'll introduce the main idea here:

• We assign each node a potential: p(x) = {2^('Z' — w) | w is exposed}. For example, if 'Y' and 'Z' are exposed, then p(x) = 1 + 2 = 3.
• We can proof p(x) <= |# of nodes of the subtree rooted by x| by proof this lemma: When we synthesis x with T1, T2, ..., Tk, p(x) <= 1 + p(T1) + ... + p(Tk). It's not hard to proof, but might have some cases to deal with.

321D - Ciel and Flipboard

For this problem we need a big "observation": what setup of "flips" are valid? What means set up of "flips", well, for example, after the 1st step operation of example 1, we get:

1 1 0
1 1 0
0 0 0

It means the left top 2x2 cells are negatived.

Given a 0-1 matrix of a set up of "flips", how can you determine if we can get it by some N x N (I use N instead of x here, it don't make sense to write something like x x x.) flips.

To solve this problem, we need the following observation:

1. For any i, any j<=x: setUp[i][j]^setUp[i][x]^setUp[i][j+x] will be 0.
2. For any i, any j<=x: setUp[j][i]^setUp[x][i]^setUp[j+x][i] will be 0.

It's quite easy to proof than find that: after each operation, there always be 0 or 2 cells lay in {setUp[i][j], setUp[i][x], setUp[i][j+x]} or {setUp[j][i], setUp[x][i], setUp[j+x][i]}.

So what? Well, then there must be no more than 2^(N*N) solutions, since if we determine the left top N x N cells, we can determine others by above equations.

And then? Magically we can proof if one set up meets all above equations, we can get it. And the proof only needs one line: think the operation as addition of vectors in GF2, then we have N*N independent vector, so there must be 2^(N*N) different setups we can get. (Yes, I admit it need some knowledge, or feeling in linear algebra)

Then the things are easy: we enumerate {setUp[1][N], setUp[2][N], ..., setUp[N][N]}, and determine others by greedy. (More detailed, by columns.)

You can find details in my code.

321E - Ciel and Gondolas

This problem may jog your memory of OI times (if you have been an OIer and now grows up, like me). Maybe some Chinese contestants might think this problem doesn't worth 2500, but DP optimization is an advanced topic in programming contest for many regions. It's quite easy to find an O(N^2 K) DP:

• dp[i][j] = max{ k | dp[i-1][k] + cost(k+1...j)}

(dp[i][j] means the minimal cost if we divide 1...j foxes into i groups)

There are many ways to optimize this kind of dp equation, but a large part of them based one the property of cost function. So we need to find some property independent of cost function.

Let opt[i][j] = the smallest k such that dp[i][j] = dp[i][k] + cost(k+1...j) Then intuitively we have opt[i][1] <= opt[i][2] <= ... <= opt[i][n]. (I admit some people don't think it's intuitively correct, but it can proof by some high school algebra)

Then how to use this stuff?

Let n = 200 and suppose we already get dp[i][j] for i<=3 and now we have to compute dp[4][j]: If we first compute dp[4][100], then we can have opt[4][100] at the same time.

And when we compute dp[4][1] ... dp[4][99], we know that the k must lay in 1...opt[4][100]. When we compute dp[4][101] ... dp[4][200], we know that k must lay in opt[4][100]...n.

Let's formalize this thing: We use compute(d, L, R, optL, optR) to denote we are computing dp[d][L...R], and we know the k must be in range optL...optR.

Then we have:

compute(d, L, R, optL, optR) = 

	1. special case: L==R.

	2. let M = (L+R) / 2, we solve dp[d][M] as well as opt[d][M]. Uses about (optR-optL+1) operations.

	3. compute(d, L, M-1, optL, opt[d][M])

	4. compute(d, M+1, R, opt[d][M], optR)

One can show that this solution will run in O(NlogN * K). Note that we don't need opt[d][M] at the center of interval optL...optR. We can proof at each recursive depth, the total cost by line 2 will be no more than 2n. And there are at most O(log(n)) depths.

Привет всем!

Не хотите ли Вы потренироваться перед предстоящим контестом ACM/ICPC Finals?

Codeforces Round #190 пройдет в пятницу, 28-го июня, в 19:30 MSK. Это последний шанс потренироваться перед финалом, не упустите его!

Я cgy4ever из Китая, и это мой первый раунд Codeforces. Я надеюсь, он понравится вам.

Как обычно, будет 7 задач: 2 для Div2, 2 для Div1 и 3 для обоих дивизионов. Я готовил эти задачи. Хотелось бы поблагодарить Gerald и sdya за тестирование задач, и MikeMirzayanov за проект Codeforces и Polygon.

Удачи и фана вам на раунде!

Update 1: The score distribution for Both Division is regular (500-1000-1500-2000-2500). The main character of all problem will be: Fox Ciel. (See here for more info)

Update 2: Also thanks Aksenov239 for helping prepared this round, including translate the problem statement into Russian. And I'm sorry for the delay of judgement at the beginning of this round. Fortunately it goes better now.