Hello, Codeforces!
Today, 17th of October at 17:35 MSK Codeforces Round #377 for second division participants will take place. As usual, first division participants are able to participate out of rating.
The round problems are taken from the problemset of regional stage of the All-Russian school team programming olympiad which was taking place yesterday in Saratov. The problemset for onsite competition was invented and prepared by Mike MikeMirzayanov Mirzayanov, Ilya IlyaLos Los, Danil danilka.pro Sagunov, Vladimir vovuh Petrov and Roman Roms Glazov. We are thankful for pre-solving competition problems to many of Saratov State U teams' participants. One problem in the round will have a bit harder version than at the competition.
Nikolay KAN Kalinin and Tatyana Tatiana_S Semenova helped us preparing problems and translating for the round — thank you! Thanks to Mike MikeMirzayanov Mirzayanov for the Codeforces and Polygon systems.
There will be 6 problems and 2 and a half hours to solve them at the round. We wish you the best luck!
If you are a participant of the yesterday competition in Saratov, please, do not register for the round and do not participate in it, also do not discuss the problems before the round ends.
UPD Scoring: 500-1000-1500-2000-2000-2500
UPD2
Congratulations to the winners!
Div.2
Div.1
As soon as the time of registration to the round was a bit early, there may be some first division participants taking part in a line with a second division participants. There are not many of them, so (and due to technical problems) this will be left as is.
Due to NEERC subregionals in Saratov, rating will be updated tomorrow.
UPD3 Editorial









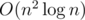 .
.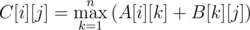
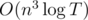 .
. solution.
solution.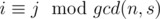 . Let's use this idea and fix
. Let's use this idea and fix 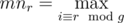 .
.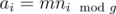 . For finding all such subarrays we will use two pointers approach and for every good
. For finding all such subarrays we will use two pointers approach and for every good 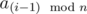 is not good we will find
is not good we will find 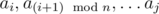 are good and
are good and 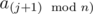 is not good. Let
is not good. Let 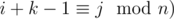 . Any it's subarray is superior, so it gives us arrays of length
. Any it's subarray is superior, so it gives us arrays of length 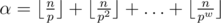 , where
, where 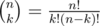 , the maximum
, the maximum 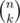 is calculated as
is calculated as 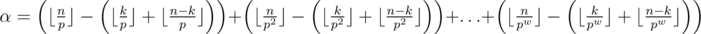 .
.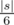 . Now, let's calculate dynamic programming on every vertex
. Now, let's calculate dynamic programming on every vertex 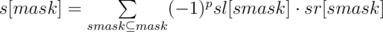 , where
, where 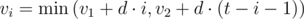 . You can iterate through
. You can iterate through 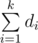 . This is easily explained by the fact that if there is a way to get the amount of
. This is easily explained by the fact that if there is a way to get the amount of 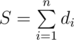 . Fix the dice
. Fix the dice  . There is also possible to get
. There is also possible to get 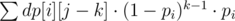 . Simple calculation of this value for each state gives
. Simple calculation of this value for each state gives 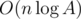 .
.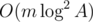 .
.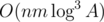 . One could notice that some of the edges are useless and reduce it to
. One could notice that some of the edges are useless and reduce it to 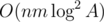 .
.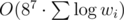 .
.
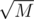 blocks containing
blocks containing 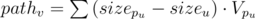 for every vertex
for every vertex 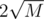 ). Next, mark every vertex being LCA of some pair of already marked vertexes, using DFS. We can prove that final number of these vertexes is at most
). Next, mark every vertex being LCA of some pair of already marked vertexes, using DFS. We can prove that final number of these vertexes is at most 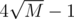 . After all this we got 'compressed' tree, containing only needed vertexes. Parent of vertex
. After all this we got 'compressed' tree, containing only needed vertexes. Parent of vertex 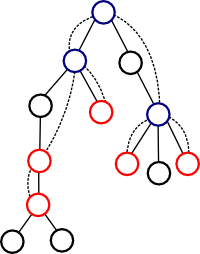
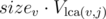 . After that, we got compressed subtree where subtree of a vertex
. After that, we got compressed subtree where subtree of a vertex 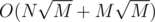 complexity, but in
complexity, but in 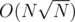 .
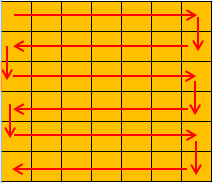
.
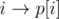 and
and 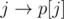 will become edges
will become edges 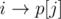 and
and 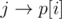 respectively. Then if
respectively. Then if 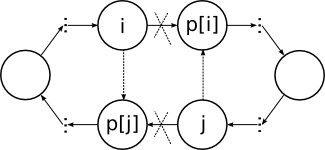
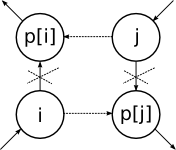
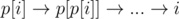 . As soon as every cycle is broken with linear asymptotics, this case solution works with
. As soon as every cycle is broken with linear asymptotics, this case solution works with  asymptotics, you may think how.
asymptotics, you may think how.
