I'm interested in whether we can Construct a tree if we know the Starting Time and Ending Time of all the Vertices.
For Example:
- Number of Vertices :4
- Starting time ST[i]:2 4 1 3
- Ending time FT[i]:2 4 4 4
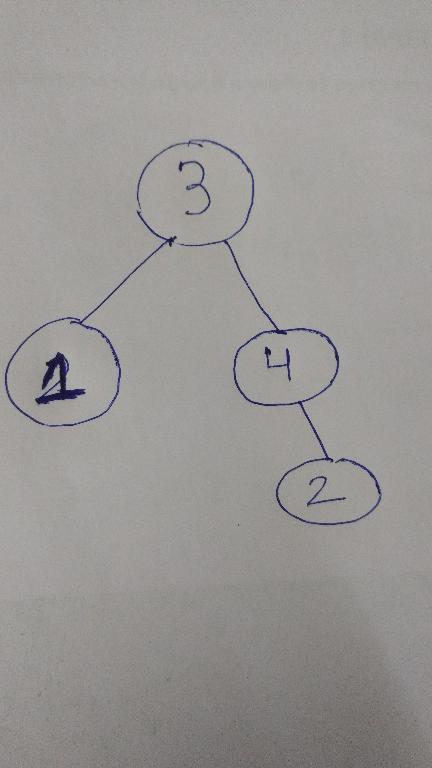
The Tree Looks Like:
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
I'm interested in whether we can Construct a tree if we know the Starting Time and Ending Time of all the Vertices.
For Example:
The Tree Looks Like:

Hello everyone,
I was working on a problem where i was given an integer p and was asked to calculate the number of digits after the decimal point in 1/p.
Ex:- Input: 100 Output: 2 as (1/100=0.01)
#include<bits/stdc++.h>
using namespace std;
int main()
{
float p;
cin>>p;
float q=1/p;
int cnt=0;
cout<<q<<"\n";
while(fmod(q,10.0)!=0)
{
q=q*10;
cnt++;
//cout<<q<<" "<<cnt<<"\n";
}
cout<<cnt-1<<"\n";
}
What i was trying to do is multiply (1/n) till it is divisible 10 and then simply print count-1 .
But the output this code is giving me is 12 in place of 2 for p=100.
Help would be appreciated :)
| Название |
|---|


