В свете происходящих сейчас законодательных мракобесий возникло настойчивое желание перевезти всё своё "хозяйство" на зарубежное доменное имя и хостинг.

Давайте попробуем поголосовать, какое название вам бы больше всего понравилось:

https://polldaddy.com/poll/7857563/

(С фантазией у меня туго, так что не стесняйтесь предлагать свои варианты — конечно, предварительно проверяя их на свободность, например, тут)

UPD Всем спасибо, голосование завершено. Результаты: победил вариант e-maxx.io (25%), вторым по популярности оказался e-maxx.us (16%).

Меня недавно спрашивали про задачу о наименьшем общем предке. А именно, о поиске LCA без какого бы то ни было препроцессинга дерева, чтобы один запрос отвечался за время O(r), где r — расстояние между вершинами запроса.

Если ограничений по памяти нет, то решение придумывается почти мгновенно: будем параллельно поднимать вверх обе вершины, и помечать в двух массивах, какие вершины мы посетили по первому пути, и какие — по второму пути. Как только мы шагнём в вершину, которая есть в обоих путях — это и есть LCA.

Но такое решение требует O(n) памяти или, если использовать hash-set, то O(r) памяти.

Мне же засел в голову такой вопрос: а есть ли решение практически без дополнительной памяти, т.е. с потреблением памяти O(1)? (Разумеется, нужно сохранить ту же временную асимптотику O(r).)

Оказалось, да. Предлагаю и вам поломать голову над этой симпатичной задачкой. (Возможно, боян? Я не встречал).

Как всегда, свои варианты решения в комментариях прячьте под правками, чтобы никто случайно не прочитал решение раньше времени.

Сегодня пришло письмо из MIT, потребовали удалить Кормена (англ. версию) и все другие книги издательства MIT.

Кормена английскую версию убрал, русскую оставил (она издавалась Вильямсом, так что напрямую, видимо, не принадлежит MIT'у).

Других книг MIT у меня вроде нет.

Но всё равно обидно.

Пользуясь случаем,

а что Вы думаете о копирайтах на научные/учебные книги?

Тема копирайта, конечно, изрядно заезжена в последнее время, но интересно мнение именно среди людей, которые более-менее часто обращаются к техническим книгам/статьям.

Моё имхо: в данном случае копирайт — это чистое зло. Авторов таких книг и статей могут поддерживать (и поддерживают) университеты.

Кроме того, зачастую университетам предоставляется бесплатный доступ к онлайн-библиотекам, а людей, готовых покупать статьи/книги, вне университетов очень мало. Следовательно, доходы от продажи должны быть весьма скромными. Кроме того, многие классические книги свободно доступны в крупных библиотеках, но чем виноваты жители провинции?

А вот вред от препятствия распространению информации — совсем немаленький. Ох, сколько раз я злился, когда не мог найти в свободном доступе те или иные статьи с алгоритмами: часто так бывает, что все современные статьи ссылаются на какую-нибудь классическую "древнюю" работу, а самой этой работы в открытом доступе как раз-то и нету.

UPD (почему-то потерялось при отправке):

Слава богу, что есть в рунете добрые люди, которые, пользуясь открытыми доступами из своих университетов, выкачивают те или иные нужные статьи. Ну разве не бред вся эта ситуация?

UPD2 стёр

Занимаясь исправлением и дополнением статьи на емаксе, с удивлением обнаружил, что, оказывается, хорошо известная нам временная оценка, данная Тарьяном ещё в 1975 г., ставится под сомнение!

На прошлом опенкапе нам "посчастливилось" обнаружить в g++ новую багу (тут предыдущая бага, которая недавно обсуждалась здесь).

Бага проявляется в сложных рекурсивных функциях при включенной оптимизации -O2.

В нашем случае это было дерево отрезков, и приводило это к неверному ответу даже на семпле (хотя без -O2 всё работает). Ещё интересным было то, что если пытаться добавить дебаг-вывод (с cout/cerr/printf) - то всё начинало работать верно :) Конечно, сами по себе эти признаки могут означать, что это кривое решение, но, по всей видимости, это не так.

В общем, после контеста минимизация нашего дерева отрезков привела к такой минимальной программе: на pastebin.

По дебаг-выводам видно, что при включении -O2 функция auxillary() вызывается два раза, один раз возвращая единицу, другой раз - ноль, а query() в итоге возвращает ноль, хотя её результат получается как сумма результатов auxillary().


Впрочем, в баг-трекере другой человек сумел сделать гораздо более простой пример: на pastebin.

Ссылка на баг здесь: http://gcc.gnu.org/bugzilla/show_bug.cgi?id=48837.

В данный момент этот баг подтверждён, а также подтверждено, что он проявляется на (!внимание!) g++ 4.3.3 - 4.6.0.

Т.е. все версии GCC за последние 2.5 года. Мда...

P.S. С подобным странным поведением решений на g++ мы сталкивались давно, но обычно как-то не придавали значения - ну, наверное, решение кривое; прошло на вижаке - и слава богу. Оказалось, что не всё так просто, и, значит, в голове надо держать ещё один фактор - кривость компилятора.

P.P.S. А на финале будет тот же g++...

Самый важный шаг на пути к решению этой задачи - понять, что достаточно рассматривать только такие повороты пылесоса, когда одна из его сторон полностью прижата к стороне комнаты.

Приглашаю на него всех школьников, только что вернувшихся из ЛКШ.Зима - чтобы не давать лишней передышки своим мозгам, а студентов - чтобы отвлечься от всех забот-хлопот, связанных с таким страшным явлением как Сессия :)

Контест окончен, в этот раз никому не удалось сдать все задачи.

Поздравляем победителя RAVEman!

Разборы задач:

• задача C
• задача D
• задача E

Кому, как мне, надоело каждый раз залогиниваться при заходе на кодфорсес (что связано с известными всем лагами и неудобствами), можно открыть в настройках браузера окно с Cookies и поставить у всех Cookie от Codeforces параметр "Expire" ("Истекает") куда-нибудь в 2015 год.

Приглашаем всех на очередной раунд Codeforces Format!

На этом раунде я буду заменять Артема Рахова в его ставшей уже привычной роли администратора контеста. Дело в том, что Артём отправился участвовать в онсайте соревнования TopCoder Open (Algorithm). Удачи, Артём! :)

Я со своей стороны постараюсь провести раунд без заминок.

Раунд окончен, результаты.

Выиграл участник с ником a4461497, а среди участников первого дивизиона - kuniavski.

Разбор задачи "B. Codeforces World Finals"

Для решения требовалось научиться проверять заданную дату XD.XM.XY на корректность (учитывая число дней в каждом месяце, високосность, и т.д.). После этого решение заключалось просто в переборе всех возможных 6 перестановок трёх чисел (BD,BM,BY), проверке каждой перестановки на корректность, и сравнении полученной даты с датой проведения финала DD.MM.YY. Сравнение можно было делать, просто прибавив 18 к числу лет, и сравнив эти две даты как тройки чисел (год,месяц,день).

Единственный случай, который вызывает вопрос, - это 29-ое февраля. Легко понять, что вышеописанное решение правильно работает в таком понимании, что несчастный, имеющий день рождения 29-го февраля, в 3/4 случаях будет отмечать день рождения 1-го марта. А вот в реальной жизни - интересно, как в таком случае поступают :)

Разбор задачи "D. Задача Царя?"

В этой задаче для правильного решения требуется следующая цепочка рассуждений (хотя, если некоторые шаги опустить или осуществить не полностью, всё равно получатся правильные решения :) ):

• Заметим, что после того, как мы пришли в город n + 1, дальнейший ответ зависит только от самого левого и самого правого из непосещённых городов (и ответом на задачу будет - пойти в ближайший к n+1-ому городу из них, а потом пойти в другой город). Отсюда сразу получаем решение для случая k = n + 1, и этот случай мы дальше не рассматриваем.
• Часть пути до города n + 1 - она покрывает какой-то отрезок городов на оси OX. Причём этот отрезок обязательно содержит точку k. Но таких отрезков может быть O(n²), поэтому пока это плохое решение.
• Можно понять, что если человек до перехода в город n + 1 как-то походил, но не посетил самый левый на оси город или самый правый, то тогда он совершил бессмысленное и невыгодное действие. В самом деле, ведь после прихода в точку n + 1 ответ будет однозначно определяться позициям самого левого и самого правого из непосещённых городов, а таким странным действием человек не изменит ни левую, ни правую границу, т.е. только ухудшит их.
• Остался случай, когда человек из города k пошёл в город n + 1 напрямик, и только потом спустился вниз. Во-первых, можно было просто вставить этот переход в программу, и больше не думать над ним :) Во-вторых, можно было всё же догадаться и доказать, что этот переход невыгоден. Для этого надо просто расписать два варианта пути: из k в n + 1, потом обратно в 1, потом в n (я считаю, что город 1 ближе к n + 1, чем n, и что k не совпадает ни с 1, ни с n), и второй вариант: из k в 1, потом в n + 1, потом в k + 1, потом в n. Выписыв явно эти две формулы, сократив одинаковые слагаемые, можно получить, что по неравенству треугольников второй вариант всегда лучше (не хуже).
• Таким образом, достаточно перебирать только два вида отрезков: [1;i] для i ≥ k, и [i;n] для i ≤ k (я считаю для удобства, что города отсортированы по абсциссе).
• Осталось аккуратно обработать каждый такой переход. Для этого перебираем все возможные i. Пусть, например, i ≤ k. Тогда надо попробовать такой переход: пойти из k в n, потом обратно в i, потом в n + 1, и потом обойти оставшуюся часть [1;i - 1]. Также обязательно надо попробовать второй переход: из k в i, потом в n, потом в n + 1, потом обойти оставшуюся часть [1;i - 1]. При i ≥ k - всё симметрично, получатся два других перехода.

Итого, не считая сортировки в начале программы (без которой, наверное, можно обойтись), получается решение за O(n).

Разбор задачи "A. Бухгалтерский учёт"

Первый способ решения: перебор

Переберём все возможные X, и проверим каждое, подходит ли оно под указанные A и B. Понятно, что имеет смысл перебирать только в тех же пределах, которыми ограничены сами A и B, т.е. от -1000 до 1000 (легко понять, что сузить эти рамки никак нельзя - для любого числа от -1000 до 1000 найдётся соответствующий тест). При фиксированном X проверять ответ надо было, n раз производя умножения, но аккуратно следя за тем, чтобы переменная не переполнилась (на что многие попадали), например, прекращая умножать, если текущее произведение уже вылезло за пределы [ - 1000;1000].

Второй способ решения: формула

Легко заметить, что если ответ есть, то это корень n-ой степени из отношения |B| и |A|, возможно, с изменённым знаком, - если A и B имеют разный знак, и n нечётно (если n чётно, то в этом случае, очевидно, ответа не будет). Поэтому можно было просто воспользоваться функцией возведения числа в степень (возводить надо было в 1 / n-ю степень), которая есть во многих языках, и проверить, что получилось целое число (разумеется, с учётом точности, - например, что оно отличается от ближайшего целого не более чем на 10^- 9).

Но здесь надо быть аккуратным со всякими нулями. Плохо, когда A = 0, и этот случай надо разобрать отдельно (B = 0 или B ≠ 0).

Вообще очень многие ошибались на тесте с A = 0 или B = 0, и если бы такие тесты не содержались в претестах, то, наверное, у половины людей задача бы упала :)

Разбор задачи "E. Хитрый и умный пароль"

Общая схема решения

Общая схема авторского решения следующая. Переберём позицию pos центра средней части middle ответа (той, которая является палиндромом). Дальше возьмём в качестве middle максимальный подпалиндром, имеющий середину ровно в позиции pos. После этого надо взять в качестве prefix и suffix такие максимальные по длине строки, что они удовлетворяют всем условиям задачи, и при этом не пересекаются с выбранной серединой.

Выполнив эту процедуру для каждой позиции pos и выбрав среди всех найденных ответов наилучший, - получим ответ на задачу.

Реализация

Фактически, задача состоит из двух подзадач:

Во-первых, определение максимальной длины палиндрома, имеющего центр в заданной позиции. Это делается за O(n) алгоритмом, описанным у меня на сайте. Иначе это можно делать с помощью бинпоиска и, например, хешей: переберём бинарным поиском эту самую искомую длину палиндрома, а внутри бинпоиска сравнивать две строки на равенство легко можно с помощью хешей (надо только посчитать два массива хешей для строки, и для её разворота).

Во-вторых, это определение длин и позиций максимальных частей prefix и suffix, не пересекающихся с заданной подстрокой [l;r]. Заметим, что если мы будем рассматривать все длины sufflen суффикса suffix в порядке увеличения, то для каждой такой длины sufflen в качестве prefix будет выгодно брать самое левое вхождение строки prefix = reverse(suffix). Таким образом, увеличивая длину suffix, мы можем сдвинуть prefix только вправо, но не влево. Обозначив через lpos[sufflen] эту самую позицию самого первого вхождения строки reverse(suffix(sufflen)), получаем, что эти lpos являются неубывающими величинами. Введём для удобства ещё величину rpos[len] = lpos[len] + len - 1 - позицию окончания вхождения этого суффикса (эти величины уже строго возрастают, как легко понять).

Итак, если бы мы знали значения этого массива lpos (а ещё удобнее - rpos), то в решении общей задачи (там, где после выбора максимального в pos палиндрома мы искали максимальные подходящие prefix и suffix) можно использовать бинарный поиск по длине sufflen (или просто предпосчитать заранее ответы на всевозможные запросы - тогда ответ на запрос будет за O(1)).

Осталось научиться считать массив lpos позиций вхождений ревёрснутых суффиксов.

Например, можно это делать хешами: пусть мы посчитали lpos[k], научимся считать lpos[k + 1]. Если строка s.substr(lpos[k], k + 1) совпадает с суффиксом длины k + 1, то lpos[k + 1] = lpos[k]. В противном случае, пробуем увеличить lpos[k + 1] на единицу, и снова выполняем сравнение, и т.д. Сравнение подстрок можно делать за O(1) с помощью хешей. И понятно, что в сумме тогда на построение всего массива уйдёт O(n) - ведь мы не могли совершить продвижений указателя вправо более, чем n раз.

Другой способ построения массива lpos, более "чёткий" - использовать префикс-функцию. Для этого сделаем строку reverse(s) + # + s, ну и просто в тех точках в правой половине полученной строки префикс-функция приняла значение k, поставить lpos[k] =  этой позиции (если, конечно, lpos[k] ещё не было присвоено какому-то другому значению - нам ведь надо искать самое первое вхождение).

Итак, в итоге довольно легко получить решение этой задачи за O(n) с помощью двух довольно известных подходов: массива палиндромностей за O(n) (алгоритм, кстати, сильно похожий на алгоритм вычисления z-функции), и хеши либо префикс-функция. Решение за можно было собрать вообще из одних хешей: ища максимальные палиндромы с помощью бинпоиска, и ища 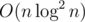sufflen тоже с помощью бинпоиска по вычисленному хешами массиву rpos.

Доказательство

Единственный неочевидный момент - почему при фиксированной pos - позиции середины центрального элемента middle - можно жадно брать максимальный палиндром с центром в ней.

Предположим противное: выгодно было брать не максимальный палиндром pal, а какой-то меньше. Посмотрим, что происходит, когда мы уменьшаем pal на единицу. Тогда длина средней части middle уменьшается на два, но зато увеличивается "свобода" для prefix и suffix. Но для каждого из них "свобода" увеличилась только на единицу: для prefix стал доступен один символ в конце, а для suffix - в начале. Значит, самое лучшее, что могло произойти, - это увеличение длины suffix на один (здесь мы пользуемся монотонностью rpos). Следовательно, при переходе от pal к pal - 1 мы потеряли два символа в длине middle, и могли выиграть максимум два символа в suffix и prefix. Значит, это уменьшение никогда не выгодно.

Другой подход к решению

Рассмотрим здесь другой способ решения этой задачи, который использовался многими участниками на контесте.

Давайте пойдём к решению с другой стороны: будем перебирать не позицию middle, а длину prefix и suffix. Теперь при фиксированных суффиксе и префиксе мы должны найти наибольший палиндром между ними, и не пересекающийся с ними.

Следует отметить, что жадность, похожая на предыдущее решение, не верна: выбрать максимальный палиндром с центром между prefix и suffix, и "обрезать" его так, чтобы он не налазил на prefix и suffix. Она неверна, потому что может быть было выгодно взять исходно не самый большой палиндром в промежутке между префиксом и суффиксом, но он станет самым выгодным после "обрезания".

Таким образом, при фиксированных префиксе и суффиксе (кстати, чтобы их зафиксировать, надо использовать какой-то из методов, описанных в предыдущем алгоритме) наша задача - научиться делать максимум в массиве палиндромностей "с обрезанием". Это значит, что поступает запрос вида "найти максимальный палиндром, целиком лежащий в отрезке [l;r]", и мы должны среди всех позиций i = l... r выбрать ту, которая даёт наибольший палиндром с центром в ней, т.е. максимизирует min(pal[i], min(r - i, i - l)). Ответить на такой запрос можно например следующим образом: будем искать искомую длину палиндрома бинарным поиском. Пусть x - фиксированная длина палиндрома внутри бинарного поиска, мы хотим проверить, есть ли такой палиндром или нет. Для этого надо проверить, есть ли на отрезке [l + x;r - x] хотя бы одно число, больше либо равное x, - а это можно сделать с помощью дерева отрезков, построенного над предварительно вычисленным массивом палиндромностей pal (как строить его эффективно, тоже описано в предыдущем алгоритме).

Тогда асимптотика решения будет , хотя её можно уменьшить до 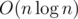, заменив дерево отрезков sparse-table (это когда для каждой позиции i и каждой степени двойки j предпосчитывают ответ на отрезке [i;i + j - 1]).

Сегодняшний контест подготовлен нами, командой Saratov SU 2 (Максим Иванов, Артем Рахов, Коля Кузнецов).

От Вас потребуется решить пять простых и не очень задачек для одного Царя, про которого вы вряд ли что-нибудь слышали раньше. Царь надеется, что задачи окажутся не очень сложными для Вас, и у него будет богатый выбор среди различных решений по каждой задаче.

UPD. Контест окончен, всем спасибо.

Таблица результатов.

Поздравляем rng_58 с победой!

Разборы задач: A, B, C, D, E.

Часто в олимпиадных задачах, чтобы оценить асимптотику алгоритма, требуется знать примерное число делителей поступающего на вход числа. Точнее, требуется знать максимальное число делителей среди всех чисел до, скажем, миллиарда.

Самая грубая оценка - O (sqrt(N)), а именно, не более двух квадратных корней из N.

Но часто это оказывается слишком грубой оценкой, неоправданно завышенной.

maths

"Страх перед нулём и единицей."

[ Dmitry Pavlov's livejournal ]

"Наша жизнь полна предрассудков и необоснованных страхов. Однако не все знают, что предрассудки и страхи во множестве присутствуют в математике. Сегодня я расскажу всего лишь про один такой предрассудок — страх перед нулём и единицей." ...

"Манифест Dieudonné («Все мы учились в одном гадюшнике…»)"

[ Dmitry Pavlov's livejournal ]

"Время от времени я начинаю разъяснять, почему геометрия, в том виде, как она сейчас преподаётся в школе, малоосмысленна, и почему ситуацию с этим необходимо менять. Вот, например, несколько недавних дискуссий, есть и другие: <links>. 

Недавно я прочитал предисловие к книге Dieudonné 1964 года Algèbre linéaire et géométrie élémentaire и обнаружил, что в этом предисловии ясно и понятно изложены все те мысли, которые я уже давно пытаюсь разъяснять в различных дискуссиях. По этой причине я решил воспроизвести русский перевод этого предисловия ниже."

science

"Обыкновенный скотч как источник рентгеновского излучения"

[ Igor Ivanov's livejournal ]

"Удивительное (и красивое!) -- рядом.

Сегодня в Nature опубликована статья, в которой рассказывается о простом эксперименте с забавными результатами. Оказывается при медленном разматывании скотча, которое происходит не равномерно, а рывками, наблюдаются короткие вспышки света. А также вспышки рентгеновского излучения с энергией в десятки кэВ!"

coding

"Программирование, как средство самовыражения"

[ a-ilyin's livejournal ]

"Это довольно большая (18кб) статья, написанная по мотивам одной дискуссии в ЖЖ. Первоначально была опубликована здесь.

 Я – как уже писал – разработчик программного обеспечения с более чем 25-летним стажем, а до этого – и параллельно с этим – был разработчиком электронной аппаратуры, как цифровой, так и аналоговой. Скажу очень кратко, что имел в том и другом некоторые успехи. ..."

humour

"Санкт-Петербурга не существует!"

[ che_telcontar's livejournal ]

"Прогуливаясь с lashner по Питеру 2 недели назад, мы занимали время словесной игрой. Потом решили выложить это в ЖЖ – в качестве доброго стёба над искателями/критиками Атлантид- Гиперборей, над альтернативными историками и «новыми хронологами». Я возвращался к тексту несколько раз и не пожалел букв. Теперь же не терпится увидеть отклики, критику и гневные опровержения. А может быть, вы найдете новые «доказательства»?"

http://code.google.com/codejam/schedule.html

На этот раз гораздо раньше всё, в мае-июне случится.

И, охохо, снова всего 25 человек в финале... Да, второй раз так вряд ли повезёт... :)