ikar's blog

Tutorial Good Bye 2013
By ikar, 11 years ago, translation, In English

Excuse me for my english, but I tried very hard to.=)

A: 379A - New Year Candles

Let cura amount of new candles, curb — amount of burnt out. Initially cura = a, curb = 0, after burning all cura new candles, amount of hours incremented by cura and curb +  = cura, lets make all burnt out candles into new cura = curb / b 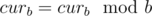, repeat this algorithm until we can make at least one new candle. #### B: 379B - New Year Present If wallet contains more then one coin, then between orders to "put a coin" we can orders to move to adjacent wallet then back. Since for each orders to "put a coin" we spend at most 2 other orders, number of total orders for maximum test equals 300 * 300 * 3 = 270000 it less then 106.

C: 379C - New Year Ratings Change

We can to sort ratings in nondecrease order, then iterate by them we can keep minimal rating not used before. If ai > cur, i's user recieve ai of rating and cur = ai + 1, else ai ≤ cur then i's user recieve cur of rating and cur increased by one.

D: 379D - New Year Letter

We can't fairly calculate sk because of length of this string which can be very large. But note that whole string not need, we just need number of AC substrings, first and last letter. That help us to easy calculate number AC substrings for any sk for some s1, s2. Let's iterate through s1, s2 using alphabet of A, C, and any other letter. We need just first and last letter and number of AC. Using some s1, s2 we can calculate sk.

E: 379E - New Year Tree Decorations

Let's keep union of first i pieces, S(i) denote the area of union for the first i pieces. Then to know visible part of i's piece we need to calculate S(i) - S(i - 1), (

Unable to parse markup [type=CF_TEX]

and with end at x = 1. Union looks like a downward convex polyline, lets represent it sequence of points, adjacent are connected. So calculate i's union, if new union will be contains new segment, this segment must intersects two segments of union, this intersection we can calculate for the amount of points in union. All points lower than new segment must be erased from union. Because each segment can add at most one point in union calculating of one range is O(n2).

F: 379F - New Year Tree

Coming soon.

G: 379G - New Year Cactus

This problem can be solved for tree by using of dynamic programming d[v][c][a], where v — vertex, c — type of vertex(whose toys are hanged or nothing are hanged there), a — number of toys hanged by Jack for this subtree, d[v][c][a] denote of maximum number of toys which can be hanged by Jill. Value d[v][c][a] can be calculated iterated through sons of v vertext and type of these vertices. Let's compress our cactus into tree by compressing each cycle into vertex. Vertex of tree will be looks like sequence of vertex from cactus which have edges not from this cycle and intermediates that belongs only to this cycle. Now we can calculate all d[v][c][a] for this tree but we must be carefully processing a vertices.

Tutorial of Good Bye 2013
  • Vote: I like it
  • +38
  • Vote: I do not like it

Comments Comments (50)
| Write comment?
»
11 years ago, # |
  Vote: I like it -6 Vote: I do not like it

problem A act optimally how to prove the algorithm acting optimmally ?

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    not really related to your question but actually a "brute-force" implementation can also AC 5571273 :)

    edit : it's clearly optimal since make new candle when ever we can, it have the same idea with the tutorial but this may be easier to understand :p

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it -11 Vote: I do not like it

      maybe it's not a good question seems trivial I think maybe the candle which is run out and then make a new one have different choice of run out candle and run out ones may have different levels and maybe not using them all in the same time or in different order maybe different. your answer is implement not brute force or exhaustion.I may have consider all the situation .I`d like an elegant simple approach to the proof.

      → Reply
»
11 years ago, # |
  Vote: I like it +10 Vote: I do not like it

This Tutorial is too simple that I can't understand how to solve D after I read it : (

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Look for example you need to calc s5 for strings s1 = CACACC and s2 = CACAA, represent s1 like 2 AC substring and first and last letter — CC,
    s2 = (1, CA)
    s3 = (3, CA) (AC + CC has no AC at the junction and we just take first and last letter)
    s4 = (4 + 1, CA) (+1 because of at the junction substring AC appears)
    s5 = (8 + 1, CA) (again).

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I got it now.

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        yes, enough to sort out first and last letter and count of AC for s1, s2.

        → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How can I obtain s1 and s2?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You could generate all strings using alphabet of 3 letters, important things in this strings would be first and last letter and amount of 'AC' substrings.

        → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Great!

      → Reply
»
11 years ago, # |
  Vote: I like it +16 Vote: I do not like it

This tutorial' english gave me cancer XD

→ Reply
»
11 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Any better explanation for problem E ?

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    You can separate the problem into K parts, because each part is independent of the others. To solve for just one part, you can keep the segments (points) that builds it, at first there is only one segment, from (xk,0) to (xk+1,0) and the area is currently 0. For each new segment (each new decoration) we must build the parts again. To add a new segment Bk, you need to check for every segment Ak that builds the part with the new segment Bk:

    • Segment A and B intersect: add the segments (A.x1, max(A.y1, B.y1)) to (intersect_x, intersect_y) and from (intersect_x, intersect_y) to (A.x2, max(A.y2, B.y2))
    • Segment A and B don't intersect: add the segment (A.x1, max(A.y1, B.y1)) to (A.x2, max(A.y2, B.y2))

    (The y coordinate for the B segment means the y for the current x). After building the parts again you have the old ones and the new ones. The amount of area that they add to the answer of this decoration is the new area minus the old area. The overall idea is not hard, it is just can be tricky to implement, specially for those who don't have much geometry skills :) (like me). You can check my code here: 5594115

    → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

i thought that struct is faster than pair,but it seems not, i changed it to pair and got ac the C problem

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What slowed you down wasn't struct, but the comparison function. See 5602813. I modified your comparison function and got AC, passing the arguments by reference and adding a "return false" at the end. Not sure why the latter is required but without it I got a WA in test #10.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      hi! thank you soo much for your explanation! its very clear and now i know where my code is wrong! it seems that it cant handle the sort when the 2 values is same, and adding "return false" seems to fix it all! thank you very much once again!

      → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    pair<int,int> is basically the same as struct {int first, int second}; with some predefined comparison operators and constructors.

    → Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Problem G how to write O(N^2) dynamic solution for tree. O(N^3) is simple, but O(N^2) is not so obvious. Answer in Russian is also acceptable.

→ Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can somebody, please, post at least a sketch of the actual solution on F? Thanks, Happy new year!

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve F?

→ Reply
»
11 years ago, # |
  Vote: I like it +8 Vote: I do not like it

How can I solve the problem F? Who can give me some idea? Thanks!

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This is a problem about LCA?

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 2   Vote: I like it +23 Vote: I do not like it

      Indeed, this is a problem about LCA. Let end_first and end_second be the endpoints of the diameter of the tree. When inserting an new node u we first have to compute the 2^j-th ancestor of u, for all j in range 0..log2(N). After that, notice that a possibly new diameter may start from j and end at end_first, or start at j and end end_second. So, you just compare the distances to get the new diameter, and you update properly end_first and end_second. I also have some code I wrote after the contest: http://mirror.codeforces.com/contest/379/submission/5603366. I hope this helps :)

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Thanks.My English is bad,but I still hope you can get gratitude from me！HaHa.

        → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        But I have another quetion now.When all nodes have two subtrees(except leaves),the height of a subtree is 1,another is [1,Q+1].In other words,the height of the new year tree is Q+2.Are you sure this solution will not be TLE？

        → Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

coming soon after X years?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve the problem F with Centroid Decomposition

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve question B?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve question F?

→ Reply