381A - Сережа и Дима
Просто проделаем все операции описанные в условии.
381B - Сережа и лесенка
Посчитаем количества каждого числа. Все различные числа, кроме максимального можно использовать не более 2-х раз. Максимальное же — только 1.
380A - Сережа и префиксы
Сгенерируем первые 100000 чисел. Будем по очереди обратывать запросы, если запрос попадает в точку доабвления 1 числа, то просто выведем его. Иначе посмотрим, какому элементу будет соотвествовать наш, и просто выведм его из предподсчитаного массива.
380B - Сережа и дерево
Сгенерируем дерево, как описано в условии. Для каждого запроса на добавление элементов. Просто для уровня будем добавлять отрезок. На запрос количества элементов будем просто проходить по всем нижним уровням, считая самую левую и самую правую вершину в поддереве. Далее для каждого уровня будем проходить по отрезкам, которые ему принадлежат и для каждого проверять — пересекается ли он с тем, что у нас сгенерирован на текущем этапе. Если да, то просто добавим элемент в множество. Сложность решения O(n·m).
380C - Сережа и скобочки
Будем поддерживать дерево отрезков, в каждой вершине будем хранить:
av — максимальную длину скобочной подпоследовательности
bv — сколько вне нее есть открытых скобок
cv — сколько вне нее есть закрытых скобок
Если нам нужно объединить две вершины с параметрами (a1, b1, c1) и (a2, b2, c2), то можно пользоваться следующими правилами:
t = min(b1, c2)
a = a1 + a2 + t
b = b1 + b2 - t
c = c1 + c2 - t
380D - Сережа и кинотеатр
Для того, что бы никто не обиделся достаточно, что бы все кроме первого человека содились возле уже сидящего. Теперь когда приходит любой челвек мы точно знаем, что по одну сторону от него никто не сидит. Будем использовать это. Будем поддерживать интервал точно занятых мест. Если первый человек не известен, то таких возможных интервала будет 2. Теперь лишь осталось аккуратно рассмотреть все случаи того как могли заходить люди, ведь на каждой итерации мы точно знаем сколько людей куда сядут.
380E - Сережа и деление
Заметим, что на любом конкретном отрезке нас интересует не более 60 чисел. Самое большое войдет в ответ с коэфициентом 1/2, следующее — 1/4, 1/8 и так далее. Таким образом для решения нужно для каждого числа знать: в сколько отрезков оно входит как максимум, как второй максимум, третий, и так далее до 60ого.
Что бы знать такую информацию достаточно найти 60 чисел больше заданого слева и справа. Это можно делать аккуратно написаным set-ом, или dsu.
Теперь имея такую информацию можно посчитать величину, которую элемент несет в ответ. Это не сложно сделать, зная позиции элементов, больших текущего. Пускай позиции элементов слева p1 > p2 > ... > ps1. А позиций справа q1 < q2 < ... < qs2. 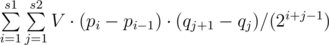 .
.
Все детали можно посмотреть в любом прошедшем решении.











Вау, да это самый быстрый разбор на свете! :)
Thanks Sereja
What a speedy tutorial!
I wonder how fast are you!
This is so obviously Google Translated. Look at the first sentence of div1 A: "100000 numbers" is translated as "number 100000". Nobody who knows English at least a little bit would reverse the order of words like that.
Needless to say, I really don't understand the solutions from it. At least I know a bit of Russian :D
Yap, it's kinnda hard to understand in this Google-Translated form. Could anybody care to take their time and rephrase the explanation a little since I had troubles solving the problem? (380A — Sereja and Prefixes). Thanks !
Here's the solution I came up with afterwards. (I think it's the same as the one described in the editorial)
First, calculate the first 105 numbers. This suffices because we know all the l's are within the range of 1 to 105, so all numbers created by the second type operation can be found in the first 105. Additionally, save the index of each of the type 1 operations. (save the position of each number)
Then, given the queries from q1 to qn, we can check two things: 1) If qi is in the set of indexes covered by type one operations, we are done. This is because we can just use a binary search to find the correct answer. 2) If qi is not, we can find which type 2 'range' qi is in. We can find the k such that k < qi < k + (cx * lx) for some x. Then, we can simply take , and this basically proves that a[qi] = a[tmp], where tmp is in the first 105 integers. (and so we can just look it up from the original calculations).
, and this basically proves that a[qi] = a[tmp], where tmp is in the first 105 integers. (and so we can just look it up from the original calculations).
sorry if the explanation isn't very good, I may revise it later.
EDIT: added latex (it says revision 8 because my internet was slow and I clicked it multiple times)
EDIT 2(9): The ranges you can calculate at the beginning, just make a matrix idx[m] and a number called curidx. When you scan in each line, you let idx[i] = curidx. Then, if it is type 1, you add one to curidx, and if it is type 2, you add c * l to curidx.
thanks for the explenation, i think it is very clear.
thanks a lot, I couldn't wrap my head around why the limit is 10**5 for storing sequence
Find out the maximum value of L .. All the array indices queried will depend on either provided value when type 1 is used as a input or on staring 1st L values when Type 2 is used .... Use a array to store 1st L values ... and Map can be used to store value larger than L when type 1 is given... Answer the query using this array or map used
в 380C: a = a1 + a2 + t
наверное имелось ввиду: a = a1 + a2 + 2*t?
А можно поподробней 380D - Сережа и кинотеатр?
В любой момент времени у нас может быть ровно 1 непрерывный отрезок сидящих людей, иначе, последний чувак, севший в интервал, занятый с двух сторон обидится.
Посмотрим, что происходит, когда чувак садится на своё заранее заданное место: один конец текущего интервала севших должен упираться в его место, иначе не получится образовать непрерывный отрезок.
Мы знаем с какой стороны от него будет этот интервал, так как мы знаем, где сидит предыдущий, севший на заранее заготовленное место.
Таким образом, у нас в каждый момент времени есть отрезок севших, и мы смотрим на следующего чувака, у которого место фиксировано: для него точно можно узнать отрезок, который получится, когда он сядет (один конец в нём, другой — запихать оставшихся в другой конец отрезка).
Осталось научиться получать из одного отрезка другой, путём приклеивания нового чувака в один из концов — это какая-то С-шка.
В начале надо ещё перебрать, с какой стороны от первого сделать отрезок.
Спасибо, стало понятней.
:o Really weird that I missed that particular solution to C, I like such tricks with segment trees. But fortunately I came up with another solution. Let's calculate two arrays sum_pref_all, sum_pref_end. In order to calculate first, change ( to 1 and ) to -1 and calculate prefixes' sums. In order to calculate second change ( to 0 and ) to 1 and calculate prefixes' sums. Answer is 2 * (sum_pref_end[r] — sum_pref_end[l — 1] — sum_pref_all[l — 1] + c) where c is equal to min(sum_pref_all[l — 1], sum_pref_all[l], ..., sum_pref_all[r]. First part sum_pref_end[r] — sum_pref_end[l — 1] is a number of all ')' in this subword and sum_pref_all[l — 1] — c is a number of ')' which can't find their corresponding '('. In order to retrieve c of course build a segment tree.
UPD: I have updated this post, since I messed up sum_pref_all and sum_pref_end in few places.
I also have a very different solution for problem C (Div1). First I used a stack in order to match each closing paranthesis to the closest unmatched open paranthesis before it (if any). In the optimal answer for any query, a closing paranthesis is either matched with that open paranthesis or with none (I did not really prove it, but it seems reasonable). Then the problem becomes: for a given query [L,R] count how many intervals [x,y] are contained within [L,R] (where x is the position of an open paranthesis and y is the position of its matching closing paranthesis, if any). In order to solve this problem easily I sorted the queries by their left endpoint and handled them in this order. I also maintained a segment tree with the right endpoints of the intervals [x,y] such that x>=L (where L is the left endpoint of the current query). Answering a query then consists of simply computing a prefix sum for the interval [1,R] (i.e. how many right endpoints of intervals [x,y] with x>=L are located before or at the position R). Note that since we sorted the queries, when advancing from one query [L1,R1] to the next one [L2,R2], we remove from the segment tree the right endpoints of intervals [x,y] with L1<=x<L2 (if any). Then, a prefix sum is actually the same as the sum over the interval [L,R] (because there will be no more right endpoints in the segment tree located before L). A binary indexed tree can also be used instead of a segment tree.
In fact, I tried very similar approach during the contest but couldn't debug it within time :(. My approach is as follows:
Let the input string be the variable str[]. For each opening bracket ('(') find the corresponding matching closing bracket (')') and store the index in an array (say store[]). This can be done using stack as mugurelionut mentioned. Now, sort the queries (L,R) using the L value.
Now consider a Binary Indexed Tree, which is initialized as follows: the value of tree[store[i]] is 1, if str[i] is '(' and it has a matching closing bracket (ie., store[i] is valid) else it is 0. Now, for each query the required answer is the 2*(prefix-sum[R] — prefix-sum[L-1]) which can be calculated easily using BIT. The catch is when moving from one query to another (note they are sorted) , say [L1, R1] to [L2, R2] where L1 <= L2, you update the value of tree[store[L1]] = 0, tree[store[L1+1]] = 0 ... tree[store[L2-1]] = 0 (update only when the store[] values are valid for the given index).
This is still O(mlogn + nlogn) because number of prefix sum queries is O(m) and number of update queries is O(n) and each query is O(logn).
Although it sounds reasonable, could you prove it formally?
I've come up with almost the same idea with you!
Is this a tutorial ?
Поправь формулу в разборе Е, там V * p[i] внутри скобок.
спасибо, поправил.
По понятнее разбор задачи 380А, пожалуйста.
Уже понял...
For problem C,
In the contest, I also used a stack to match the paranthesis first, but then I chose an O(nsqrtn) approach (how stupid) which ultimately got me a TLE. QAQ.
Yes, O(N*sqrt(N)) was too much for this problem (with N being 1 million). But still, it might be an interesting an approach. Can you share it with us?
Sure~
The first part was exactly the same as "First I used a stack in order to match each closing paranthesis to the closest unmatched open paranthesis before it (if any). In the optimal answer for any query, a closing paranthesis is either matched with that open paranthesis or with none (I did not really prove it, but it seems reasonable)." :P
Then sort the queries by "Build sqrt(n) bucket due to the left point, put query [l,r] into (l/sqrt(n)+1)-th bucket, inside each bucket sort the queries by the right point" (also known as Mo Dui's algorithm in Chinese), and then brute-forced through all the queries using two pointers, checking whether a pair of paranthesis was added or deleted.
OK, I got it. So for the current bucket (containing the left endpoints of some queries) you can maintain the number of pairs of parantheses fully contained in buckets to its right (and up to the right endpoint of the current query). Then, you would consider the positions between the left endpoint of the current query and the end of its bucket (or the right endpoint of the query, whichever comes first) to check for possible extra pairs of parantheses starting there and contained in the query interval. At least that's how I would implement it and it would lead to an O(N * sqrt(N)) time complexity : O(N) for each bucket containing left endpoints of some queries, plus O(sqrt(N)) per query. I don't see how you would use the two-pointer algorithm, as the left endpoints of the queries from the current bucket are not also sorted (so you might have to go back and forth with the pointer pointing to the left endpoint of the current query — but that wouldn't be a problem, as this wouldn't amount to more than O(sqrt(N)) per query, anyway).
yes, the point for this algorithm is for the two pointers to go back and forth, but the time compensation would still be O(NsqrtN) ~
anyway, choosing this algorithm in this precise problem just seems a bit going too far... :(
I don't understood DIV2-D problem.Can it be solved with DP?
I know that it has been said already, but it's almost impossible to read this kind of tutorials in English (I mean when it's google translated). I would volunteer to translate the solutions from Russian to English, shouldn't take that much time and effort :)
I really cannot understand Sereja's D1-C solution at all. Could someone explain it? What are really stored in each of the segment tree nodes?
b : number of unused '('
c : number of unused ')'
a : number of "()"
for each interval (l, r) you can match X of '(' in interval (l, mid) with ')' in interval (mid+1, r).
and X = min(number of unused '(' in (l, mid), number of unused ')' in (mid+1, r)).
so for interval (l, r)
a(l, r)= a(l, mid) + a(mid+1, r) + X;
b(l, r)= b(l, mid) + b(mid+1, r)- X;
-X because we used X of them and made X "()".
c(l, r)=c(l, mid) + c(mid+1, r)- X;
in 380C can someone explain how is this case handled with segment tree?
left Node = ( ) ) => a = 2, b = 0, c = 1
right Node = ) ( ) => a = 2, b = 0, c = 1
par Node = ( ) ) ) ( ) => a = 2, b = 0, c = 2
but above explanation will give X = 0, a = 4, b = 0, c = 2
In the parent node, a=4.
a is the longest matching subsequence, not substring
thanks, i was solving the question assuming it to be substring. very bad:(
Задача с префиксами. "Иначе посмотрим, какому элементу будет соотвествовать наш" — как это понимать? Ведь это спуск за O(m) — не пройдёт по времени. UPDПонял.
Подсказка: 1 ≤ li ≤ 105
Объясните задачу Div.1 C, пожалуйста. Я вообще не понял разбор.
Другое решение:
Пусть у нас есть строка и мы хотим найти длину наибольшей правильной подпоследовательности.
Посчитаем баланс для каждой позиции строки.
Давай попробуем узнать сколько из закрывающих скобок мы точно не сможем использовать:
это будет
max(0, -minimum_balance).Хотелось бы узнать сколько из открывающих мы точно не сможем использовать.
Мы только что сделали тоже самое для закрывающих, тогда давайте перевернём строку, поменяем местами
(и)и посчитаем количество, как в предыдущем пункте.Оказывается, что ответ — это длина строки минус 2 предыдущих найденных величины.
Реализация
Не могу спокойно смотреть, когда слово "оказывается" употребляется в подобном контексте.
Пусть
min— минимальный баланс на отрезке[l, r], аb[]— массив балансов. Тогда если из отрезка удалитьb[l] - minпервых закрывающих скобочек, то баланс всех префиксов станет не меньше, чемb[l]. Аналогично, если удалитьb[r] - minпоследних открывающих скобок, то баланс всего отрезка окажется не больше, чем баланс любого префикса. При этом, баланс всего отрезка окажется равен нулю. Поэтому удалитьb[l] + b[r] - 2*minскобочек не только необходимо, но и достаточно.В задаче С я почему-то подумал, что нужно найти самую длинную подстроку, а не подпоследовательность. Ничего не придумал. А есть ли решение такой задачи за разумное время?
Можно попробовать за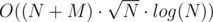
Определим f(pos) для открывающей скобки как позиция соответствующей ей закрывающей в проходе всей строки со стеком. Также определим link(pos) как f(pos) + 1 или - 1, если f(pos) не определена. Любая правильная скобочная подстрока с концами в l и r имеет вид: l → link(l) → link(link(l)) → ... → link(link(...)) = r + 1. Также посчитаем link(pos, p) = (2p раз пройти по link(pos)).
Разобьём строку на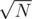 блоков и для каждой пары блоков посчитаем длину наибольшей подстроки, которая начинается в одном блоке и заканчивается в другом: перебираем начало строки в первом блоке и двоичным подъёмом по link подбираем наибольшую правую границу, которая не вылезает за правый блок (или возьмём посчитанный ответ для 2х вложенных отрезков блоков).
блоков и для каждой пары блоков посчитаем длину наибольшей подстроки, которая начинается в одном блоке и заканчивается в другом: перебираем начало строки в первом блоке и двоичным подъёмом по link подбираем наибольшую правую границу, которая не вылезает за правый блок (или возьмём посчитанный ответ для 2х вложенных отрезков блоков).
Теперь надо обработать запрос [l, r]:
Если l и r лежат в одном или соседних блоках, то посчитаем ответ стеком в лоб.
Иначе попробуем взять как ответ предпосчитанное значение для блоков, которые полностью лежат в [l, r].
Теперь переберём начало ответа в левом блоке и двоичным подъёмом найдём наибольшую подстроку, которая не вылезает за r.
После этого переберём конец ответа в последнем блоке и также найдём для каждого конца наибольшую подстроку, которая не вылезает за l (для этого нужно посчитать linkrev(pos, p) — тоже самое, что link(pos, p), только смотрим назад).
Кажется, можно за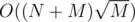 .
.
Если посчитать баланс balance[i] каждой позиции i от начала последовательности, то получится что для каждого запроса с параметрами (l, r) мы должны найти две позиции l' ≥ l, r' ≤ r, такие что balance[l'] = balance[r'], баланс внутри найденного отрезка не меньше чем на границе, и r' - l' максимально.
Выберем в последовательности k равномерно отстоящих друг от друга позиций checkpoint[j](j = 0..k - 1), будем считать, что каждой позиции checkpoint[j] соответствует кусок от checkpoint[j - 1] + 1 до checkpoint[j].
Для каждой закрывающей скобки(в позиции i) найдем максимальный идущий от неё к началу интервал, на котором баланс не меньше, чем в ней. Так как последовательность балансов в каком-то смысле непрерывна, то чтобы найти для закрывающей скобки ближайшую позицию, в котором баланс меньше, нужно просто найти, где находится ближайшая позиция с балансом balance[i] - 1. Это можно сделать за один проход по последовательности храня для каждого баланса, где он последний раз встретился. То же самое сделаем для открывающих скобок в сторону конца.
Теперь само решение: будем идти от конца к началу(от позиции n - 1 до позиции 0, пусть в данный момент мы находимся в позиции i), постепенно отвечая на запросы, и все время поддерживая в checkpoint'ах лучшую на данный момент подстроку, которая начинается не раньше позиции i и заканчивается где-то в его куске.
Когда мы только пришли в позицию i, мы должны пересчитать лучшие значения в checkpoint'ах, они могли изменится, только если в ответе задействована позиция i, для этого для каждого checkpoint'а, мы должны определить ближайшую слева к нему позицию с балансом balance[i](тут есть некоторые подводные камни, например, чтобы это сделать быстро, нужно изначально для каждого баланса выписать все места, где он встречается и оставить в списке только те, которые являются ближайшими к checkpoint'у(таких будет не больше k) + если окажется, что внутри отрезка есть позиция i' с балансом меньше, чем balance[i], то для одного из checkpoint'ов нужно взять максимальную(но не большую, чем i') позицию с balance[i]). Обновление работает за O(K)
Когда мы хотим обработать запрос, то мы должны пройтись по всем checkpoint'ам + возможно наш ответ попал в кусок, который заканчивается между двумя checkpoint'ами, для этого куска нам нужно в каждой его позиции найти самую левую с таким же балансом, но так чтобы между ними баланс был не меньше, это делается с помощью вспомогательной части, которая перед решением. Ответ на запрос работает за O(K + N / K).
Получается решение за O(NK + M(K + N / K)). При K2 = M получается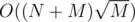 , что может быть даже уложилось бы в time limit при текущих ограничениях.
, что может быть даже уложилось бы в time limit при текущих ограничениях.
Ещё, наверное, можно за O((N + M)·logN), если я нигде не наврал:
Посчитаем также link(pos), link(pos, p), linkrev(pos) и len(pos), lenrev(pos) — наибольшая длина подстроки, которая начинается/заканчивается в позиции pos. Сделаем дерево отрезков по len и lenrev.
Теперь запрос [l, r]:
найдём максимум на этом отрезке по len — этот максимум может вылезать за r, тогда обрежем его двоичным подъёмом. После этого мы получили [l ≤ l', r' ≤ r]. Ответ может лежать либо в [r' + 1, r], либо в [l, l' - 1].
Попробуем взять в ответ максимум по lenrev на [r' + 1, r] — он точно не вылезет за r', так как он лежит внутри первого не взятого блока для изначально найденного ответа. (Имеется в виду, что если link(pos) = R, то все link(pos < i < R) < R, тоже самое для linkrev).
Ещё попробуем взять в ответ максимум по len на [l, l' - 1]: он не вылезет за r, так как если он вылезает, то он содержит в себе изначально найденный ответ (либо изначальный ответ является продолжением нашего, либо изначальный ответ лежит внутри блока нашего ответа), в любом случае, тогда бы наш ответ являлся глобальным максимумом ещё на первом шаге.
Ответом я называю последовательность pos → link(pos) → link(link(pos)) → ...
Блоком ответа я называю отрезок между pos и link(pos), между link(pos) и link(link(pos)) и т.д.
А если последовательность такая(запрос выделен квадратным скобками)?
[(()])
Тогда максимум по len в первой круглой скобке и её блок вылезает за пределы запроса, при этом link, я так понимаю, нам не поможет, так как он ссылается на конец последовательности?
Так как максимум сразу вылезает, то l' = r' = 0 (не можем взять ни один блок), тогда мы посмотрим на максимум по lenrev на отрезке [1, 2] и найдём linkrev[2] = 0, то есть найдём ( ( ) ).
Согласен, все похоже на правду.
UPD: Может быть зря согласился :) А что насчет такого?
Я ведь правильно понимаю, что когда max len не подходит мы пытаемся найти max по lenrev на всем отрезке?
Нет, максимум по lenrev мы ищем на [r' + 1, r] — то есть правее того места, где мы обломались, проходя по link.
В примере выше найдутся все 2 ответа :)
Максимум по len на всём отрезке: ([())|(()])|, не можем пройти ни один блок, значит смотрим максимум по lenrev на ([())(|()|]). Находим, то что находим.
Потом смотрим на максимум по len на ([|())|(()]). Опять находим ()
Судя по всему, если r' выступает за r, то max(maxlenrev(l' + 1..r), maxlen(l..l' - 1)) будет достаточно. Так что, я все же соглашусь с решением.
Ну я писал, что мы обрезаем ответ, так что r' ≤ r.
А так всё хорошо :)
UPD: всё-таки брать max по lenrev на отрезке [l', r] плохо, так как он может вылезти за левую границу:
пример: (([))(())((])).
[l', r'] -- (([))|(())|((]))
В тоже время lenrev восьмой скобки указывается в начало строки.
Ну так я предложил брать максимум на отрезке [l' + 1, r] только в том случае, если r' выступает за r. Может быть, я неправильно понял, что такое r', но я думал, что это граница после уменьшения её до тех пор, пока она не влезет.
Да, r' — та самая граница после уменьшения.
Она не может вылезать, за r.
Наверное, ты имеешь в виду брать максимум на [l' + 1, r], если первый же блок вылезает за r, но в таком случае l' = r'.
И я не очень понял, как может быть, что
r' выступает за r, еслиэто граница после уменьшения её до тех пор, пока она не влезет.380C — Sereja and Brackets I think a = a1 + a2 + t
should be a = a1 + a2 + 2*t
Else you can output
2*aat the outputAlso storing
ais not required as it is:length_of_sequence - b - cIn the problem C: 380C — Sereja and Brackets,
It should be a = a1 + a2 + (2)*t instead of a = a1 + a2 + t
Or still: a = a1 + a2 + t, then output 2*a.
I have seen some DP solutions for problem C Sereja and Brackets. Can anyone explain how a DP solution would work?
PS: BTW, the tutorial quality is very poor (at least the English version).
I think the problem author should give his tutorial to somebody who can translate that in English, just similar as preparing problems. Hope there won't be more google translated, unreadable tutorials in the future
380A — Sereja and Prefixes
why can the kth of element, kth can be fit in 64-bit integer ?
Kth can't but size of arr can!
Can the problem Sereja and Brackets be converted into an equal problem of : Given a set or intervals and queries (of type l_i and r_i), find the number of intervals within that range ?
I know this is very old, but it may help someone that's studying: on problem Sereja and Brackets there is a way easier solution. The key observation here is that the closing bracket will be chosen greedly, that is, the last opened bracket can be closed with the first available bracket everytime, yelding the optimal bracket matching for any query. That observation being made, the problems is reduced to counting the matchings inside the interval of the query. I did this by first storing the right side of each query in it's corresponding position and then sweeping the string from left to right, keeping a Fenwick Tree (BIT) for the matchings: when a left bracket finds a closing bracket, I add 1 to the position of the left bracket. When I hit a spot that contains some query end, I answer this query with RSQ(Li,Ri).
Here is the pseudocode:
And here is my AC submission: 7108258
nice solution .
deleted
This blog is really helpful for those struggling to understand the editorial for 380C — Sereja and Brackets . Also a great resource to learn Segment Trees.
In Div1C — Sereja and Brackets, what if, instead of a subsequence, a substring is asked? How would we proceed?
I misread the problem and was trying to solve this problem, but couldn't find a very efficient merge function in the segment tree that could solve this problem with the given constraints. I'm curious if there is a way...
u basically kesp track of minimum prefix, and final sum , the minimum should be non negative, and sum should be 0 , which can easily be merged with segment trees and by sum i also mean this, if its an opening bracket u add 1, else u subtract 1
In sereja and brackets ~~~~~ struct Info{ int open,close,full; Info(int _open,int _close,int _full){ open=_open; close=_close; full=_full; } }; vector<Info*>segtree; string s; Info * merge(Info * left,Info * right){ int open=left->open+right->open-min(left->open,right->close); int close=left->close+right->close-min(left->open,right->close); int full=left->full+right->full+min(left->open,right->close); Info*ans=new Info(open,close,full); return ans; } void build(int index,int st,int en){ if(st==en){ segtree[index]=((s[st]=='(')?new Info(1,0,0):new Info(0,1,0)); return; } int mid=(st+en)/2; build(2*index,st,mid); build(2*index+1,mid+1,en); segtree[index]=merge(segtree[2*index],segtree[2*index+1]); } Info* query(int index,int st,int en,int l,int r){ if(st>=l && en<=r) return segtree[index]; if(st>r || en<l) return new Info(0,0,0); int mid=(st+en)/2; return merge(query(2*index,st,mid,l,r),query(2*index+1,mid+1,en,l,r)); } void solve() {
cin>>s; s=" "+s; int n=sz(s); n--; segtree=vector<Info*>(4*(n)); fo(i,4*(n)) segtree[i]=new Info(0,0,0); build(1,1,n); int m; cin>>m; while(m--){ int a,b; cin>>a>>b; cout<<(query(1,1,n,a,b)->full)*2<<"\n"; }}
void solve() {
cin>>s; s=" "+s; int n=sz(s); n--; segtree=vector<Info*>(4*(n),new Info(0,0,0)); build(1,1,n); int m; cin>>m; while(m--){ int a,b; cin>>a>>b; cout<<(query(1,1,n,a,b)->full)*2<<"\n"; }} ~~~~~ this passes. I dont understand the difference between the two.
hi, can anyone explain me why Im having the wrong answer on test 3? I can't figure it out. here is my code:
void sort(int array[], int size) { int i,j; for(i = 0; i < size — 1; i++) { for(j = 0; j < size — 1 — i; j++) { if(array[j] < array[j+1]) { int temp = array[j]; array[j] = array[j+1]; array[j+1] = temp; } } } }
int main() { int n,i; int sumD = 0, sumS = 0;
scanf("%d", &n); int *arr = (int *)malloc(n * sizeof(int)); for(i = 0; i < n; i++) { scanf("%d", &arr[i]); } sort(arr, n); int k = 0; int m = 1; while(k < n) { sumS += arr[k]; k += 2; } while(m < n) { sumD += arr[m]; m += 2; } printf("%d %d", sumS, sumD); return 0;}
In 380C, I get TLE on test 12; help me, please :
include <bits/stdc++.h>
using namespace std;
struct node { int mo, dg, ca; int l,r; node () { mo = dg = ca=0; l=r = 0; }
}; node operator+(node a, node b) { node t; t.l = a.l; t.r = b.r; t.ca = a.ca + b.ca; int tc; tc = min(a.mo,b.dg); t.ca += 2*tc; t.mo = a.mo — tc + b.mo; t.dg = a.dg + b.dg — tc;
typedef vector tnode; void maketree (tnode &tr, string s, int id, int l, int r) { tr[id].l =l; tr[id].r = r; if (l == r){
if (s[l-1] == '(') tr[id].mo = 1; else if (s[l-1] ==')') tr[id].dg = 1; return; } int m = (l+r)/2; maketree(tr,s,id*2, l,m); maketree(tr,s,id*2+1, m+1,r); tr[id] = tr[id*2] + tr[id*2+1]; return; } node getcap (tnode tr, int id, int u, int v) { node t; if (tr[id].l>v || tr[id].r<u) return t; if (tr[id].l>=u && tr[id].r<=v) return tr[id]; return getcap(tr, id*2, u,v) + getcap(tr, id*2+1,u,v); } int main(int argc, char const *argv[]) { ios_base::sync_with_stdio(false); cin.tie(NULL); // freopen("380c.inp","r", stdin); string s; cin>>s; int q; cin>>q; tnode st(4*s.size()); maketree(st,s,1,1,s.size()); while (q--){ int u,v; cin>>u>>v; node re =getcap(st,1,u,v); cout << re.ca <<endl; } return 0; }
Can someone say why am I getting a TLE on tc13 , I have used the usual segment tree approach for solving it . 271336839