| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
Расскажите, пожалуйста, или дайте ссылку, где можно почитать про O(E) алгоритм поиска узкого остовного дерева.
Узкое остовное дерево неориентированного графа G есть остовное дерево G, в котором наибольший вес ребра минимален среди всех возможных остовных деревьев.
Этот коммент можно не читать
Возможно, тем, что он работает не за O(E)? :)
мне кажется алгоритм должен выглядеть как алгоритм поиска к-той порядковой статисткики по ходу дела нужно поддерживать DSU (возможно с "откатами", т.е. уметь отменять добавление рёбер до некоторого старого значения). т.е. примерно такая рекурсия. разбиваем рёбра на две половины так, что в первой половине рёбра имеют меньшие веса, чем во второй. добавляем рёбра с меньшими весами в DSU, если у нас осталось одно множество, то надо взять поменьше рёбер. если несколько множеств, то побольше. Неуверен, но кажется можно такое реализовать за O(E)
Блин :D
вроде можно, да?
Да, можно. DSU с откатами нужен. то есть запоминаем какие значения в массиве мы меняли на какие, и потом в обратном порядке выполняем замены.
Если делать DSU с откатами, то нельзя применять эвристику сжатия путей. Или я не прав?
Я слабо в теме разбираюсь, а почему нельзя изменения эти тоже в стек записывать, а потом откатить?
почему нельзя?
код
Меня тут умные люди поправили, что от эвристики сжатия путей не будет никакого толка, так как доказательство её эффективности основывается на факте, что ранг родителя только растёт. При откате это условие перестаёт выполняться. Вы можете проверить на больших тестах, даёт ли прибавку в скорости эта эвристика.
Привет) Меня тут попросили уточнить, уточняю:
На случайных тестах сжатие путей дает выигрыш. На не случайных не дает. Не случайный тест:
Построили join-ами полное бинарное дерево. При этом соединяли мы всегда корни, поэтому сжатие путей ничего не сжало.
Породили новую версию.
Сделали в новой версии запрос от листа за время Theta(logn).
goto 2
Спасибо за уточнения. Наш случай отличается от общего тем, что мы не откатываем изменения после одного запроса за O(log(N)), мы выполняем серию запросов. Допустим на самом первом шаге рекурсии мы построили полное бинарное дерево из N/2 вершин. в следующем шаге рекурсии у нас есть E/2 запросов, и их суммарная стоимость не сможет быть N logN из-за сжатия путей на этом шаге. Тем не менее имхо асимптотика ухудшилась и стала нелинейной(не могу оценить достоверно).
А что если безоткатно сжимать пути перед вызовом рекурсии? т.е. для множества вершин из рёбер [L, R) вызвать Get и забыть про эти изменения.
Посмотрел исходную задачу. Решается она так. Найдем вес max ребра:
Ищем ребро-медиану за O(E)
Проверяем за O(V+E) меньше ответ медианы или больше. Для этого за O(V+E) сжимаем компоненты связности, образованные ребрами меньшими медианы. И за O(E) для всех больших медианы ребер проверяем, соединяют ли они разные компоненты.
Делаем за O(V+E) переход к задаче с E/2 ребрами. Если ответ меньше медианы, выкинем все ребра большие медианы. Если же ответ больше медианы, сожмем компоненты связности, получим новый граф.
Чтобы всё это решение работало за O(E) достаточно поддерживать V = O(E). Нужно после каждого уменьшения задачи выкидывать вершины степени 0 и перенумеровывать оставшиеся.
Как по весу max ребра восстановить дерево, думаю, понятно.
Сойдет? =)
По поводу СНМ: когда я пытаюсь думать, как бы соптимизить сжатие путей, чтобы получилась линия, я получаю именно описанное выше. Сжимать, так сжимать!
Оффтоп: раз уж зашла речь о к-той порядковой статистике, дайте пару задач на неё, чтоб сдать можно было. Спасибо.
Фигня, потому что откатывать нельзя.
Спасибо Eledven.
1) делим ребра на 2 равных множества, так что веса ребер в первом не больше весов во втором;
2) проверяем, не образуют ли остов ребра из первого множества;
3) если образуют, то рекурсивно находим ответ для данного подграфа;
4) если не образуют, то рассматриваем граф из сконденсированных несвязанных компонент и ребер из 2-го множества.
5) на последнем шаге алгоритма мы соединим ребром две оставшихся компоненты; вес этого ребра будет ответом на задачу.
статья с этим алгоритмом опубликована Камерини в 78-м году
статья в википедии: http://en.wikipedia.org/wiki/User:Yuxwiki/Camerini%27s_algorithm
Я так понимаю, что основное свойство этого алгоритма, заключается в том, что ребро вес которого равен величине узкого остовного дерева всегда передаётся в следующий рекурсивный вызов.
Доказательство: Пусть это будет ребро e. Пусть e попало в сконденсированную компоненту. Очевидно, что существует цикл c, состоящий из ребёр вес которых меньше чем вес e. Добавим этот цикл в узкое остовное дерево T, заменим e на любое ребро из цикла c, а остальные рёбра из цикла почистим без нарушения связности. Очевидно, что тогда T не узкое остовное дерево.
Минимальное основное дерево является узким. Допустим, что это не так. Тогда, удалим из минимального дерева самое большое ребро. Оно разбилось на две компоненты. Между ними есть путь в узком. Посмотрим на ребро пути, которое не лежит в минимальном. Оно меньше удаленного, потому что иначе минимальное было узким. Но тогда минимальное не было минимальнм, потому что если удалить самое большое и добавить это, получится меньше.
Но мы не можем найти минимальное остовное дерево за O(E). Сортировка рёбер портит оценку.
А как же фибоначчиева куча и не очень плотные графы?
всмысле алгоритм крускала на фибоначчиевой куче? O(E) вроде не достигнуть.
наверное имелось ввиду через алгоритм Прима. его ещё можно через sqrt-декомпозицию за
.
Да, конечно Прима, оговорился.
Можно за O(E) в среднем. Почитать можно вот тут.
узкое дерево не обязательно является минимальным. Кстати, его легко найти за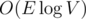
— бинпоиском по весу максимального ребра
Извиняюсь за минус, не сразу понял что Вы написали.
Под логарифмом значится V — число вершин? Как сделать бинпоиск с LogE понятно, а LogV не очень.
Ну log E = O(log V), когда нет кратных ребер. Если кратные ребра есть — от них можно избавиться за ElogV опять же
Ты прав, но указание V под логарифмом могло иметь именно такой смысл, что мы ищем в диапазоне из V весов.
Для теста из 3х вершин и ребер (x = 1, y = 2, w = 1) (x = 1, y = 2, w = 2) (x = 2, y = 3, w = 100). Можно выбрать и не мин остов. То есть это доказательство только в одну сторону. Может этим можно как то пользоваться?
http://e-maxx.ru/algo/mst_prim
Вместе с примером выходит, что MST сильнее узкого ST.