Hello Everyone!
I Think Problem D in Div 2 RD225 = problem B in Div 1 RD225 too hard!!! because just 46 person got AC (2 person in Div 2 & 44 person in Div 1 !!)
and if you have some algorithm for this problem that got AC please share it here!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Hello Everyone!
I Think Problem D in Div 2 RD225 = problem B in Div 1 RD225 too hard!!! because just 46 person got AC (2 person in Div 2 & 44 person in Div 1 !!)
and if you have some algorithm for this problem that got AC please share it here!
| Name |
|---|



It's mentioned that
My idea was:
in each row, there are "good" intervals of cells that we can get to from (1, 1)
a volcano splits a good interval into 2 (one or both possibly empty); if there's no volcano between 2 cells from different good intervals, they're merged (more generally, if we can get to some cell, we can get to all cells to its right until a volcano (or the border of the map)
simulating this process efficiently (using set<>s for non-empty good intervals) for all rows is enough for comparably large n and m; for n large, merge chunks of empty rows into one
there are at most O(m) non-empty good intervals; each volcano now leads to operations that take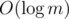 time; the same time is taken by merging 2 good intervals, and there are O(m) empty rows (after the above mentioned merging), so the time is
time; the same time is taken by merging 2 good intervals, and there are O(m) empty rows (after the above mentioned merging), so the time is 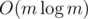
I think my idea is right but i overlooked something.
If you imagine a graph where each node is a volcane and two volcanes share an edge if they share a common point, then you only need to check if (1, 1) is cut-off from (n, n).
You do this my imagineing that walls are also nodes in the graph and checking if coresponding walls are connected.
Edit: nevermind i got it, where i was wrong.
That was my idea at first. Remember 325D - Reclamation? There was also this problem where you needed to find the smallest square such that blocking (free) cells in such square will separate the top left and bottom right corner, and it used a similar idea.
I soon found a test case where this approach failed :D
Well, my idea came from http://www.spoj.com/problems/DINOSM/
But i forgot that the guy from problem statement can only move down and right...