Can be solved offline in $$$\mathcal{O}((n+q)\log n)$$$ using segment tree (just scale segment endpoints or use implicit segment tree). Sort queries by their starting endpoints (break ties arbitrarily). Let $$$a$$$ be an array (initially filled with zeros). For every segment $$$(l_i, r_i)$$$ increment $$$a_{r_i}$$$ by 1. Now, iterate through queries. You start at point $$$1$$$. In order to answer queries for segments $$$(1, r_i)$$$ you need to find sum $$$a_1+a_2+\dots+a_{r_i}$$$ (which can be done in $$$\mathcal{O}(\log n)$$$ using segment tree). Then, let's say there was a segment starting at $$$1$$$ and ending in some $$$r_i$$$. Obviously, it will never be in an answer to any other query, thus we can easily erase it (decrement $$$a_{r_i}$$$ by 1). Every segment will be added and removed only once thus final complexity is $$$\mathcal{O}((n+q)\log n)$$$

Let's take all segments and sort them by their left endpoint (break ties arbitrarily, scale them before). Now, take all segments (sorted) and create an array $$$a$$$ where $$$a_i = r_i$$$ (i.e. $$$i$$$-th element of this array corresponds to right endpoint of $$$i$$$-th segment in sorted order). Given a query $$$(l, r)$$$ we need to binary search on segments to find first segment with $$$l \leq l_i$$$ (Let's say it is $$$x$$$-th segment). The problem thus reduces to finding the number of elements less than or equal to $$$r$$$ on suffix $$$(x, \dots)$$$. You can use Wavelet tree to do the job in $$$\mathcal{O}(\log^2 n)$$$ per query so final complexity is $$$\mathcal{O}((n+q)\log^2 n)$$$.

PS. (Maybe there is a way to exploit the fact that we are doing queries on suffixes and not intervals, but I cannot think of anything clever right now).

Problem 6

The problem: for each query, find the number of fixed paths nested in the queried path.

Let's run Euler tour of the tree and record for each node $$$v$$$ the time we entered it $$$(tin[v])$$$ and the time we left it $$$(tout[v])$$$. Consider a fixed path $$$(u, v)$$$, where $$$tin[u] < tin[v]$$$ (I assume $$$u ≠ v$$$ for any fixed path).

There are 2 cases:

Case 1. $$$u$$$ is not an ancestor of $$$v$$$ (i.e. $$$LCA(u, v) ≠ u$$$). Then, any queried path that contains $$$(u, v)$$$ must start in the subtree of $$$u$$$ and end in the subtree of $$$v$$$. Note that for any node $$$x$$$ in the subtree of $$$u$$$, $$$tin[x] ∈ [tin[u], tout[u]]$$$. So $$$(u, v)$$$ will be nested in the queried path $$$(x, y)$$$ iff $$$tin[x] ∈ [tin[u], tout[u]]$$$ and $$$tin[y] ∈ [tin[v], tout[v]]$$$ or vice versa.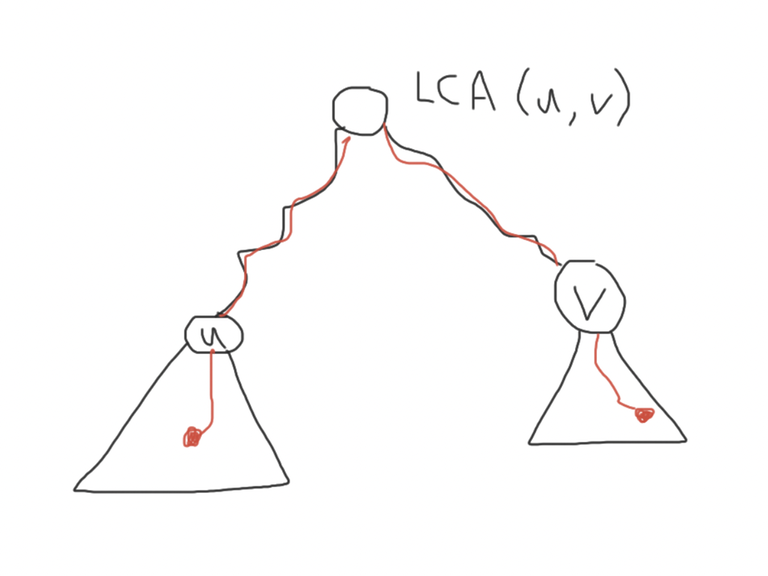

Case 2. $$$u$$$ is an ancestor of $$$v$$$ (i.e. $$$LCA(u, v) = u$$$). Let $$$w$$$ be the highest ancestor of $$$v$$$ below $$$u$$$. $$$w$$$ can be found using binary lifting in $$$O(log \;n)$$$ per path ($$$O(n \; log \; n)$$$ pre-processing is needed). It is easy to see that a queried path contains $$$(u, v)$$$ iff it starts in the subtree of $$$v$$$ and ends outside the subtree of $$$w$$$. So $$$(u, v)$$$ will be nested in the queried path $$$(x, y)$$$ iff $$$tin[x] ∈ [tin[v], tout[v]]$$$ and $$$tin[y] ∈ [0, tin[w] - 1] ∪ [tout[w] + 1, 2n - 1] $$$ or vice versa.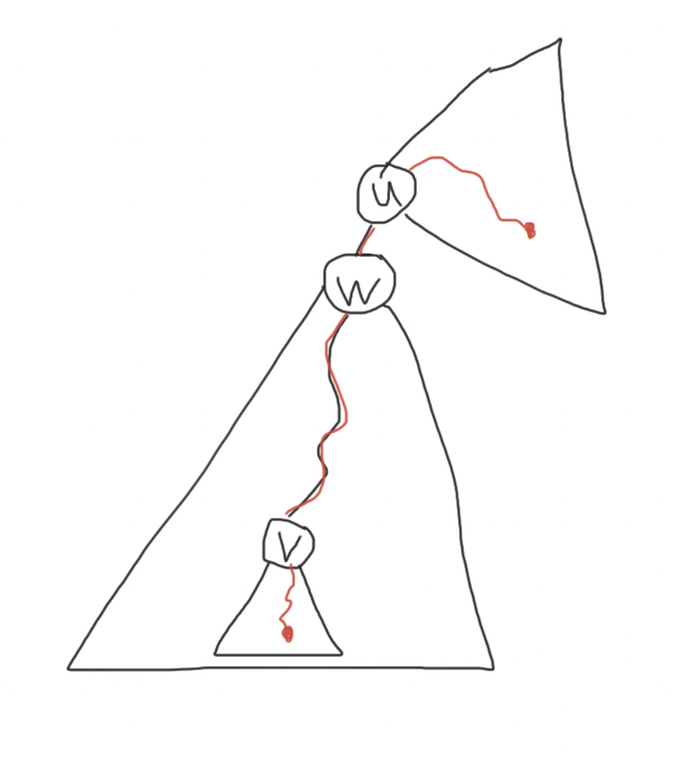

Any queried path $$$(x, y)$$$ can be represented as a point with coordinates $$$(tin[x], tin[y])$$$. Then, any fixed path creates 1 or 2 ranges for both coordinates, effectively making 1 or 2 rectangles on the plane. The answer to the query is the number of rectangles containing the queried point. This quite classical problem can be solved off-line using a difference array and a Fenwick tree in $$$O(q \; log \; n)$$$. So the total time complexity of the solution is $$$O((n + q) \; log \; n)$$$ and memory is $$$O(n \; log \;n)$$$. However, memory is $$$O(n \; log \; n)$$$ just because of the binary lifting construction, which is needed to find $$$w$$$. This subproblem is just a Level Ancestor problem and can be easily solved off-line in $$$O(n + q)$$$, e.g. by maintaining a vector of nodes on the path from the root to each vertex, so the needed $$$w$$$ can be accessed by a single array index in $$$O(1)$$$. This optimization would reduce memory complexity to $$$O(n)$$$.

See the code of the unoptimized $$$O((n + q) \; log \; n)$$$ solution below:

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 20, NN = 2 * N, LOG = 18;

vector<int> g[N];
int tin[N], tout[N], timer;
int par[N][LOG];
vector<pair<pair<int, int>, int>> bal[NN];
vector<pair<int, int>> queries[NN];
int ans[N];

void dfs(int v, int p){
  tin[v] = timer++;

  par[v][0] = p;
  for (int i = 1; i < LOG; i++) par[v][i] = par[par[v][i - 1]][i - 1];

  for (auto u : g[v]){
    if (u != p) dfs(u, v);
  }

  tout[v] = timer++;
}

bool is_anc(int u, int v){
  return tin[u] <= tin[v] && tout[v] <= tout[u]; // Returns true if u is ancestor of v
}

int lift(int u, int v){
  // Lift u to the highest node before v
  for (int i = LOG - 1; i >= 0; i--){
    if (!is_anc(par[u][i], v)) u = par[u][i];
  }
  return u;
}

void add(int l1, int r1, int l2, int r2){
  bal[l1].push_back(pair{pair{l2, r2}, +1});
  bal[r1 + 1].push_back(pair{pair{l2, r2}, -1});
}

int bit[NN];

void add(int idx, int delta){
  for (; idx < NN; idx |= idx + 1) bit[idx] += delta;
}

int sum(int r){
  int res = 0;
  for (; r >= 0; r = (r & r + 1) - 1) res += bit[r];
  return res;
}

int main(){
  int n, m, q;
  cin >> n >> m >> q;
  // n - no. of vertices, m - no. of fixed paths, q - no. of queries
  for (int i = 1; i < n; i++){
    int a, b;
    cin >> a >> b;
    g[a].push_back(b);
    g[b].push_back(a);
  }
  dfs(1, 1);
  while (m--){
    int u, v;
    cin >> u >> v;
    assert(u != v);
    if (tin[u] > tin[v]) swap(u, v);
    if (is_anc(u, v)){
      int w = lift(v, u);
      add(tin[v], tout[v], 0, tin[w] - 1);
      add(tin[v], tout[v], tout[w] + 1, NN - 2);
      add(0, tin[w] - 1, tin[v], tout[v]);
      add(tout[w] + 1, NN - 2, tin[v], tout[v]);
    }
    else{
      add(tin[u], tout[u], tin[v], tout[v]);
      add(tin[v], tout[v], tin[u], tout[u]);
    }
  }
  for (int i = 0; i < q; i++){
    int a, b;
    cin >> a >> b;
    queries[tin[a]].push_back({tin[b], i});
  }
  for (int i = 0; i < NN; i++){
    for (auto [p, delta] : bal[i]){
      auto [l, r] = p;
      add(l, delta);
      add(r + 1, -delta);
    }
    for (auto [x, id] : queries[i]){
      ans[id] = sum(x);
    }
  }
  for (int i = 0; i < q; i++) cout << ans[i] << endl;
}