Hello, Codeforces!
Recently I was solving problems on data structures from the archive, and I came up with ideas for several problems. I would like to share them with you and get your opinion on them. This blog is indirectly inspired by similar blog by BERNARD. I will also be very happy if you suggest solutions to problems (faster than $$$O(nq)$$$) or their modifications in the comments. Any feedback is very important!
Anyways, let's move on to the tasks.
Problem 1. There is a set of $$$n$$$ segments given by the boundaries $$$l_i$$$ and $$$r_i$$$ ($$$0$$$ <= $$$l_i$$$ <= $$$r_i$$$ <= $$$10^9$$$). There are also $$$q$$$ queries, each defined by a segment with boundaries $$$x_i$$$ и $$$y_i$$$ ($$$0$$$ <= $$$x_i$$$ <= $$$y_i$$$ <= $$$10^9$$$). For each query, you need to find the number of segments nested in the query segment.
Problem 2. Similar to problem 1, but there are queries of adding segments to the set.
Problem 3. Similar to problem 2, but there are queries of removing segments from the set (it is guaranteed that the segment to be removed is in the set).
Problem 4. Similar to problem 2, but after adding a segment, a new version of the set is created and you need to answer online queries for a specific version of the set.
Problem 5. Similar to problem 1, but in 2D/kD (i.e. the set consists of rectangles on the plane, you need to find the number of rectangles on the query rectangle).
Problem 6. Similar to problem 1, but instead of segments we will use simple paths in the tree, it is necessary to find the number of paths nested in the query path.
Problem 7. Similar to problems 1-4, but each segment has its own weight and it is necessary to find not the number, but the minimum / maximum among the weights of the nested segments.
Problem 8. Similar to problem 7, but you need to find the number of different weights of nested segments.
Problem 9. Similar to problem 7, but you need to find the median / k-th statistics by the weights of the nested segments.
Problem 10. There is a set of $$$n$$$ segments on the coordinate plane given by two points whose coordinates do not exceed $$$10^9$$$. It is necessary to answer queries for the number of segments from the set in the rectangle.
Problem 11. Similar to problem 10, but you need to be able to perform the same operations as in problems 1-4 and 7-9.











P1. $$$\mathcal{O}((n+q)\log n)$$$, offline
Can be solved offline in $$$\mathcal{O}((n+q)\log n)$$$ using segment tree (just scale segment endpoints or use implicit segment tree). Sort queries by their starting endpoints (break ties arbitrarily). Let $$$a$$$ be an array (initially filled with zeros). For every segment $$$(l_i, r_i)$$$ increment $$$a_{r_i}$$$ by 1. Now, iterate through queries. You start at point $$$1$$$. In order to answer queries for segments $$$(1, r_i)$$$ you need to find sum $$$a_1+a_2+\dots+a_{r_i}$$$ (which can be done in $$$\mathcal{O}(\log n)$$$ using segment tree). Then, let's say there was a segment starting at $$$1$$$ and ending in some $$$r_i$$$. Obviously, it will never be in an answer to any other query, thus we can easily erase it (decrement $$$a_{r_i}$$$ by 1). Every segment will be added and removed only once thus final complexity is $$$\mathcal{O}((n+q)\log n)$$$
P2 (and also P3 actually). $$$\mathcal{O}((n+q)\log^2 n)$$$, offline
Let's take all segments and sort them by their left endpoint (break ties arbitrarily, scale them before). Now, take all segments (sorted) and create an array $$$a$$$ where $$$a_i = r_i$$$ (i.e. $$$i$$$-th element of this array corresponds to right endpoint of $$$i$$$-th segment in sorted order). Given a query $$$(l, r)$$$ we need to binary search on segments to find first segment with $$$l \leq l_i$$$ (Let's say it is $$$x$$$-th segment). The problem thus reduces to finding the number of elements less than or equal to $$$r$$$ on suffix $$$(x, \dots)$$$. You can use Wavelet tree to do the job in $$$\mathcal{O}(\log^2 n)$$$ per query so final complexity is $$$\mathcal{O}((n+q)\log^2 n)$$$.
PS. (Maybe there is a way to exploit the fact that we are doing queries on suffixes and not intervals, but I cannot think of anything clever right now).
P1-P3 can all be solved online with an ordered set on a segtree. I believe 1, 2, 3, 4, 7, 8, 9 can all be solved using 2d segtree
Problem 6
The problem: for each query, find the number of fixed paths nested in the queried path.
Let's run Euler tour of the tree and record for each node $$$v$$$ the time we entered it $$$(tin[v])$$$ and the time we left it $$$(tout[v])$$$. Consider a fixed path $$$(u, v)$$$, where $$$tin[u] < tin[v]$$$ (I assume $$$u ≠ v$$$ for any fixed path).
There are 2 cases:
Case 1. $$$u$$$ is not an ancestor of $$$v$$$ (i.e. $$$LCA(u, v) ≠ u$$$). Then, any queried path that contains $$$(u, v)$$$ must start in the subtree of $$$u$$$ and end in the subtree of $$$v$$$. Note that for any node $$$x$$$ in the subtree of $$$u$$$, $$$tin[x] ∈ [tin[u], tout[u]]$$$. So $$$(u, v)$$$ will be nested in the queried path $$$(x, y)$$$ iff $$$tin[x] ∈ [tin[u], tout[u]]$$$ and $$$tin[y] ∈ [tin[v], tout[v]]$$$ or vice versa.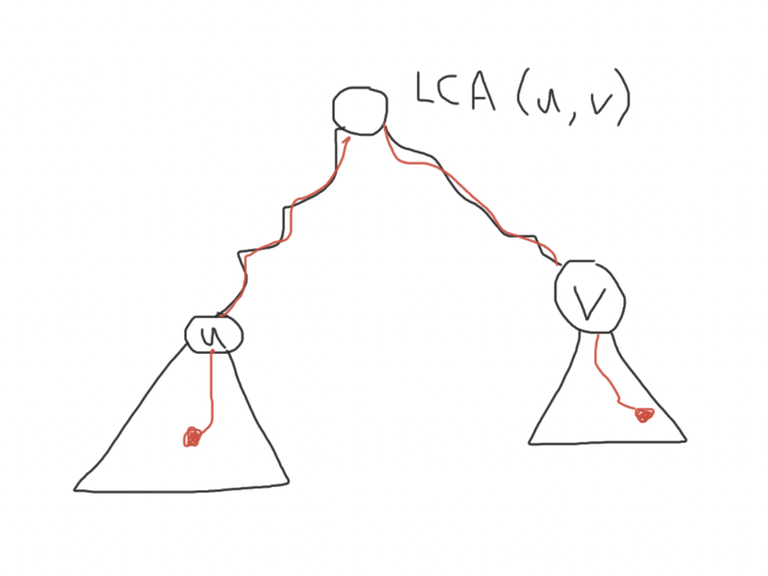
Case 2. $$$u$$$ is an ancestor of $$$v$$$ (i.e. $$$LCA(u, v) = u$$$). Let $$$w$$$ be the highest ancestor of $$$v$$$ below $$$u$$$. $$$w$$$ can be found using binary lifting in $$$O(log \;n)$$$ per path ($$$O(n \; log \; n)$$$ pre-processing is needed). It is easy to see that a queried path contains $$$(u, v)$$$ iff it starts in the subtree of $$$v$$$ and ends outside the subtree of $$$w$$$. So $$$(u, v)$$$ will be nested in the queried path $$$(x, y)$$$ iff $$$tin[x] ∈ [tin[v], tout[v]]$$$ and $$$tin[y] ∈ [0, tin[w] - 1] ∪ [tout[w] + 1, 2n - 1] $$$ or vice versa.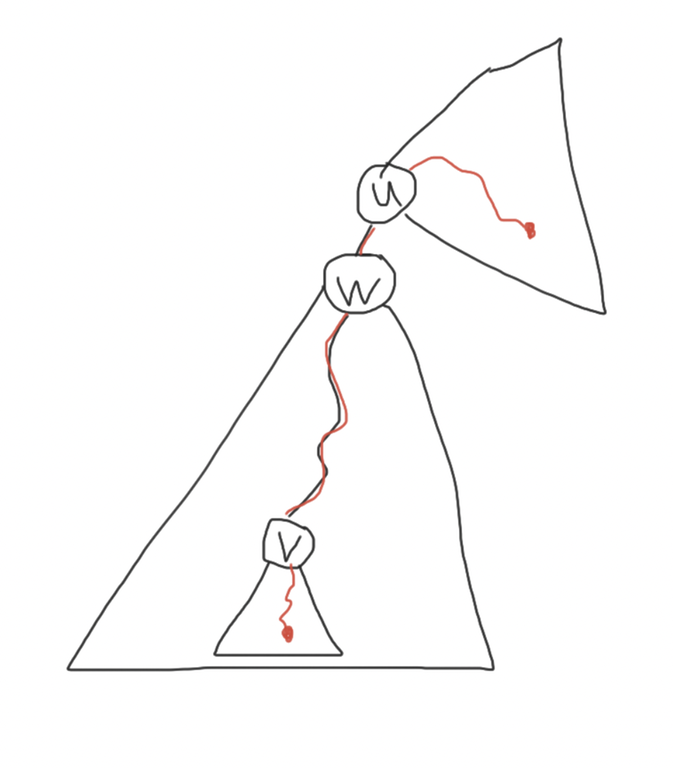
Any queried path $$$(x, y)$$$ can be represented as a point with coordinates $$$(tin[x], tin[y])$$$. Then, any fixed path creates 1 or 2 ranges for both coordinates, effectively making 1 or 2 rectangles on the plane. The answer to the query is the number of rectangles containing the queried point. This quite classical problem can be solved off-line using a difference array and a Fenwick tree in $$$O(q \; log \; n)$$$. So the total time complexity of the solution is $$$O((n + q) \; log \; n)$$$ and memory is $$$O(n \; log \;n)$$$. However, memory is $$$O(n \; log \; n)$$$ just because of the binary lifting construction, which is needed to find $$$w$$$. This subproblem is just a Level Ancestor problem and can be easily solved off-line in $$$O(n + q)$$$, e.g. by maintaining a vector of nodes on the path from the root to each vertex, so the needed $$$w$$$ can be accessed by a single array index in $$$O(1)$$$. This optimization would reduce memory complexity to $$$O(n)$$$.
See the code of the unoptimized $$$O((n + q) \; log \; n)$$$ solution below: