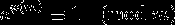Hi, I am having problem with solving this task from my math homework. If number p is prime and p^2+8 is also prime. Prove that p^3+4 is also prime number.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 11:56:59 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Suppose that p ≠ 3. Then thus p2 + 8 is not prime and we were wrong in our assumption. Then p = 3 and p3 + 4 = 31 which is obviously prime.
thus p2 + 8 is not prime and we were wrong in our assumption. Then p = 3 and p3 + 4 = 31 which is obviously prime.
How to prove that p2 = 1 mod 3?
Fermat's little theorem. If p is prime, then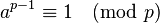
This is a special case of Euler's theorem, which is formulated like this for coprime a, m: