omg hi Codeforces!
I've been meaning to write a blog about this interesting, but not (as far as I know) documented trick for a while. I've decided to call it the Amogus trick after the first problem where I encountered and used it.
Prerequisites
- DSU
- Basic knowledge of 2-SAT (definitely not required, but it may make the blog easier to understand)
Focus Problem: 1594D - The Number of Imposters
First, let's solve an easier version of this problem, where we just need to find whether there exists a configuration of player roles (i.e. Crewmate or Imposter) such that all the statements made by players so far are true.
Let's look at the two different types of statements made by players separately.
Case 1: Player $$$i$$$ claims Player $$$j$$$ is a crewmate. Now, if Player $$$i$$$ is a crewmate, Player $$$j$$$ will also be a crewmate. Similarly, if Player $$$i$$$ is an imposter, Player $$$j$$$ will also be an imposter. The reversed versions of these statements are also true. Using this, we can create a virtual "edge" between Players $$$i$$$ and $$$j$$$, as their roles in the game will always be the same. More formally, for those familiar with 2-SAT or otherwise, we create the equivalency $$$v_i = v_j$$$.
Case 2: Player $$$i$$$ claims Player $$$j$$$ is an imposter. Now, if Player $$$i$$$ is a crewmate, Player $$$j$$$ will be an imposter. Similarly, if Player $$$i$$$ is an imposter, Player $$$j$$$ will be a crewmate. We can create a virtual "anti-edge" between Players $$$i$$$ and $$$j$$$, as their roles in the game will always be the different. More formally, we create the equivalency $$$v_i = !v_j$$$.
Adding edges is easy, we can just use normal DSU. But how do we deal with anti-edges? This is where the Amogus Trick comes in!
We can deal with these anti-edges by creating a DSU with $$$2n$$$ nodes, where nodes $$$1$$$ to $$$n$$$ represent player $$$i$$$ being a crewmate, and nodes $$$n + 1$$$ to $$$2n$$$ represent player $$$i - n$$$ being an imposter. Now, let's look at those cases again.
Case 1 results in both players having the same role in the game. Therefore, when such a statement is said, we can unite nodes $$$i$$$ and $$$j$$$, and similarly, unite nodes $$$i + n$$$ and $$$j + n$$$.
Case 2 results in both players having differing roles in the game. Therefore, when such a statement is said, we can unite nodes $$$i$$$ and $$$j + n$$$, and similarly, unite nodes $$$i + n$$$ and $$$j$$$.
Testcases 2 & 3 of the sample input in the problem, respectively, visualised with the Amogus trick:
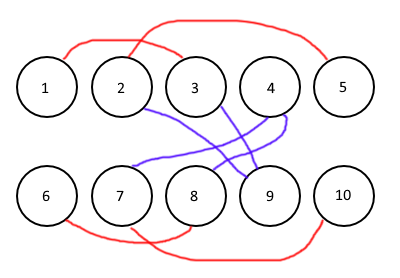
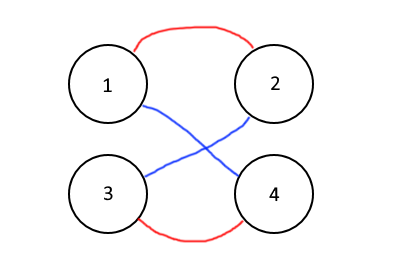
So, how can we solve our reduced problem with this? Note that a player can be exactly one of $$$\{ \text{Crewmate, Imposter} \}$$$, so a configuration is invalid iff for some $$$1 \le i \le n$$$, nodes $$$i$$$ and $$$i + n$$$ are in the same component in our DSU. This is the only condition we need to check, as since the edges we add to our DSU are symmetric, there will always be a valid assignment of roles.
It's not too difficult to extend this idea to solve our original problem.
Using this trick, we can solve a variety of other problems, such as dynamic bipartiteness checking, and it can often be paired with other modifications of DSU such as with support for rollbacks.
Other Problems:
Problems are ordered (roughly) in ascending order of difficulty.
A special thank you to kostia244, BucketPotato, fishy15 and AlperenT for providing lots of feedback and/or sample problems!











Best trick name doesn't exi-
Imagine trying to tell someone about this trick without amusing them
Player $$$i$$$ claims Player $$$j$$$ is a crewmate. ... Similarly, if Player $$$i$$$ is an imposter, Player $$$j$$$ will also be an imposter.
I don't think this is true
Why not?
(from the problem statement)
Oh I did not read this and thought we were talking about actual Among Us :)
No problem, good catch though, I didn't realise it was unclear, edited it :)
More problems solvable with this idea:
- 1615D - X(or)-mas Tree
- 1594D - The Number of Imposters
- 1385G - Columns Swaps
- 776D - The Door Problem
- INOI 2021 Among Us
You can search for my submission to see how.
if player $$$i$$$ is an impostor, player $$$j$$$ can be anything
Hi, see zscoder's comment and its replies :)
I also thought we were talking about actual Among Us :)
Auto comment: topic has been updated by ScarletS (previous revision, new revision, compare).
阿嬷古斯
It would be even better if there's a problem with this trick and the author calls the input format "SUSNF (SUS Normal Form)"
I have always solved such problems by maintaining a coloring within the DSU, maintaining for each vertex in the forest whether its color is different than or the same as its parent.
This is more extensible than the 2-SAT type of reasoning, because you can keep all sorts of data in the links of the DSU, while "amogus trick" can really only be about 2-SAT. For example, 1074D - Deduction Queries comes to mind.
Another similar problem: https://dmoj.ca/problem/noi01p1
ඞ
Good explanation! Recently I was solving https://mirror.codeforces.com/contest/1713/problem/E where the official solution used a similar trick, but wasn't explained in as much detail.
The solution I came up with was more dumb/straightforward.
You can use the "naive DSU" — store a vector of connected components, and when merging, move the smaller component to the larger one. Store the colors (0 or 1) of each element in a separate array, initialized to 0. Then, when merging, compare the colors of the two elements you are joining, and if they don't match, flip all the colors of the smaller component.
You pay a factor of O(log N) but it doesn't require coming up with a clever trick. In general, this naive DSU is very flexible — you can store and update whatever info you want about individual vertices, and you have the explicit connected components as well.
Hi. Sorry for necroposting, but your code on Cross Swapping fails if we change
dsu.unite(i, j + n);in line 46 todsu.unite(j + n, i);on the following testcase:Thanks for pointing that out! Yeah, in this case, the order of the arguments in "unite"/"merge" is actually important, as we're utilising the property that if we do the operations in the way in the code, the nodes in the DSU will be symmetric (for example, if node $$$i$$$ is a parent node, then node $$$i + n$$$ will also be a parent node. Similarly, if node $$$i$$$ is not a parent node, then node $$$i + n$$$ won't be parent node). Performing the operations in this way ensures the symmetric property remains.
You can also resolve this by making the DSU unite/merge implementation order-deterministic, for example, by adding the lines
at the start of it, so the arrangement of nodes in the DSU remains the same regardless of $$$unite(x, y)$$$ or $$$unite(y, x)$$$ calls.
Oh this explains everything. Thank you !