This (quite sudden) post is about a data structure I have came up with in one day in bed, and this won't be a full series(I am yet a student, which means I don't have time to invent data structures all day and all night). Still, Thinking about this, I thought it would be a good idea to cover it on its own post. So here we are.
Concept
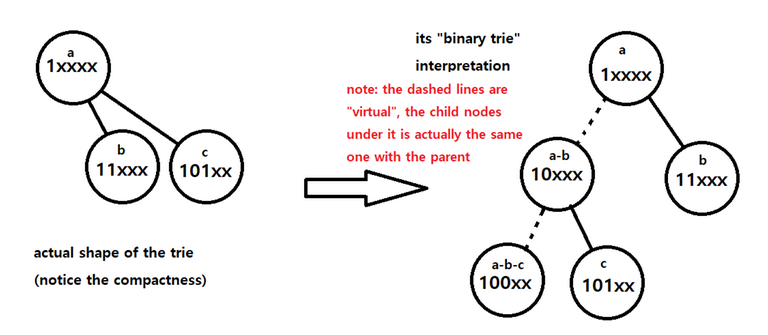
The traditional bit trie uses one leaf node for one number, and every leaf node has same depth. but about this, I thought — why? "Do we really have to use $$$32$$$ zeroes, just to represent a single zero? Heck no. There has to be a better way." And this is where I came up with this idea.
Instead of using the same old left-right child, let's use up to $$$l \leq depth$$$ children for one node. $$$l$$$ is the suffix part when each node represents a prefix. For every prefix node, we connect prefix nodes with only one $$$1$$$ bit determined after the current prefix. For example, under $$$1\text{xxxx}_2$$$, there are $$$11\text{xxx}_2$$$, $$$101\text{xx}_2$$$, and etc. Then, while the undetermined suffix (ex. the $$$\text{xxx}$$$ in $$$1\text{xxx}_2$$$) is, of course, undetermined, we can assume they are $$$0$$$ for the exact node the prefix exists on. Then we can use the prefix node $$$1\text{xxxx}_2$$$ for $$$10000_2$$$ also.
The Important Detail
At this moment, you should be wondering, how do we distinguish the node for the number $$$10000_2$$$ and the prefix $$$1\text{xxxx}_2$$$? They use the same node after all. My conclusion? You don't need to. To do this, you can just save the size (amount of elements) of the subtree. Now, let us denote the size of the subtree of prefix $$$S$$$ as $$$n(S)$$$. then $$$n(1\text{xxxx}_2) = n(11\text{xxx}_2) + n(101\text{xx}_2) + \ldots + n(10000_2)$$$ applies. So you can just traverse the child nodes one by one, and the rest is the number itself.
Traversing the Bit-indexed Trie
Using the "important detail" stated above, traversing the Bit-indexed Trie boils down to simply interpreting it like a binary tree. We start at the root, which is $$$0$$$, and we can interpret this node as $$$0\text{xxxxx}_2$$$. This root node may (or may not) have $$$01\text{xxxx}_2$$$ as a child node. Important point here is to keep a variable for the size of the "virtual" subtree of the current node. (we will denote this as $$$c$$$.) If the subtree size of the current node ($$$0\text{xxxxx}_2$$$) is $$$s$$$ and that of the right child node ($$$01\text{xxxx}_2$$$) is $$$s_1$$$, then the subtree size of the left child node, when interpreted as a binary trie, should be $$$s-s_1$$$. So if we want to traverse towards the right child node, do so, and update $$$c$$$ to $$$s_1$$$. On the other hand, if we want to traverse towards the left child node, stay on the current node, assume that we did move ($$$0\text{xxxxx}_2$$$ yet shares the node with $$$00\text{xxxx}_2$$$), and update $$$c$$$ to $$$c-s_1$$$. After understanding this, almost everything goes same with the usual trie.
Interesting stuff about the Bit-indexed Trie
With the fact that a single number is represented as a single node in the data structure, we can use a hash table to represent the whole trie. And what's so great about this method? It lies in its simplicity. Let's assume the trie is represented with a unordered_map<int,int> type. (the key is for the node, the value is for the subtree size) Now inserting a value in the trie is as simple as this:
and that is it! Simple, isn't it? and here comes the reason I named the data structure "Bit-indexed Trie". Many should have noticed the similarity of the name with the Bit-indexed Tree, also known as the Fenwick Tree. (I could not call it the Fenwick Trie, Peter Fenwick simply did not make it) The Bit-indexed Trie even has many common facts with the Bit-indexed Tree! Here are some:
- It can replace the traditional bit trie, similar to how the BIT replaces the Segment Tree in many situations.
- It reduces the memory usage from $$$2M$$$ ~ $$$4M$$$ to $$$M$$$, as they save values in every node, not only the leaf nodes.
- They have very similar implementation in many parts, see the snippet above.
also, as we saved the subtree sizes, accessing the subtree size information turns out to be almost $$$O(1)$$$ (assuming the nodes are saved in a data structure with $$$O(1)$$$ random access). Even if you don't make it $$$O(1)$$$, I believe the improvements will be quite significant, as it would be possible to optimize some processes with __builtin_clz and such bitmask functions.
EDIT: errorgorn and Kaey told me that finding the amount of numbers with a certain prefix is not $$$O(1)$$$, and they are correct. It turns out to be $$$O(\text{number of trailing zeroes in the prefix})$$$.
Summary
In this post, I covered the concepts and details of the data structure I have come up with, which makes it possible to reduce the memory usage in a bit-trie to half of the usual trie or even further. I look forward to release a full C++ implementation of it soon, and I hope many people would notice the beauty of this data structure. Thank you for reading.











If you have any suggestions to either improve or extend the data structure or have found any problems in the explanation, please post in the comments.
Isn't all of this quite pointless if you have a ds with $$$O(1)$$$ random access? You just use it instead of the trie and it will surely be better, since there will be $$$O(N)$$$ nodes in the trie.
Good point, but I meant that if this $$$O(1)$$$ random access ds could represent the whole tree (which it does), it can both be traversed like a trie and accessed directly for certain functions (ex. How many numbers inserted in the trie have a certain prefix?). However, as we are using this to do what we could do with tries, the ability to be traversed like a normal trie is still needed.
ok nvm i just forgot what the point of a trie is, btw time complexity for point query (# of strings with a certain prefix) is the number of its trailing 0s, so $$$O(1)$$$ average and $$$O(logN)$$$ worst case. Gj and sorry for my comment.
Ah, true. I think I forgot to think about counting "unique" numbers with a certain prefix, I just counted duplicates in the answer, so in this case the subtree size is just the answer.
I don't understand what advantage we gain from using this compared to the traditional trie (for subtree size, we can add $$$O(1)$$$ random access DS to it if we really wanted).
Sure, you may be able to represent numbers with many 0s efficiently, but how about the number lf 1s? If the input data contains many 1s, you don't have any significant speedup compared to the traditional trie.
Although it is true that BITs are faster than segment trees, it is because most segment trees uses a recurisve implementation while BITs are coded iteratively, not because BITs use less memory. I believe the iterative segment tree have a similar runtime to BITs (source, actually faster, for some cursed reasons). Using $$$O(1)$$$ random access data structures is surely slower than traditional trie which only uses array acceses.
Furthermore, we made the structure of the trie really complicated which might be hard to work with for non-trivial problems.
Can you demonstrate a problem (possibly one that you made yourself) where there is significant performance boost?
There are some cases, though rare, where you can cheese the whole limit into an array, say, $$$A_i \leq 2^{25} - 1$$$. This was the case when I first came up with this idea. The performance side was still a hypothesis, yet I do think in most cases it improves the "average" performance, assuming every bit of the integer is randomly decided (in this case, the depth would be almost halved)
That's literally a vanilla BIT... I don't think we shoukd talk about such things when discussing tries as tries are only used when size of values are large
I agree, but do remember that $$$O(1)$$$ random access is extremely slow compared to array accesses.
Edit: Also I realized your subtree size might not be $$$O(1)$$$. How do you find people with mask
100...00XX...XXin constsnt time with the values you have saved?One thing to note: You don't have to use an $$$O(1)$$$ random access ds! You can still use the array method, only difference is that you traverse to $$$\text{trie}[\text{index}][\text{msb excluding prefix}]$$$ instead of $$$\text{trie}[\text{index}][\text{next bit}]$$$. The $$$O(1)$$$ random access ds example was just an example of how it could be implemented, I would recommend using the array method if you are used to it. One thing that bothers me though, is the size of the array. Would there be an upper bound to the size of the array required? I think changing $$$\text{trie}[32N][2]$$$ to $$$\text{trie}[16N][32]$$$ would make it overwhelmingly large and completely cancel out the purpose of this data structure (saving memory).
reading the edit, I think you completely caught me there. This case totally slipped my mind, and that case shows the worst case where the time complexity is $$$O(\text{number of trailing zeroes in the prefix})$$$.
Auto comment: topic has been updated by chromate00 (previous revision, new revision, compare).
Auto comment: topic has been updated by chromate00 (previous revision, new revision, compare).
Me when recursive acronym