Hi there,
I hope you all are doing very good. Today, I had a discussion with my friend. He was asked below mathematical problem in his SDE interview by the technical team. But, he was not able to come up with any solution of that problem. Later, when he discussed that with me. I think I was able to solve 1st part of the problem, but I too got stuck on the 2nd part. So, Kindly help us in understanding what should be the solution of the 2nd part of the below problem.
Problem:
Given P = A*B*C, where A = 3y, B = 2y+1, and C = 2^y
Also, some value K is given, which is fixed. And, it is obvious that for all y>0, value of P will increase. So, we need to answer two parts:
- (i) Find the minimum value of y such that P>=K in O(logK) time.
- (ii) Find the minimum value of y such that P>=K in O(log(logK)) time.
My Solution of 1st part: Since for all y>0, value of P is increasing. So, we can apply binary search here. We will start range of y from 1 to infinity, and we will check if P>=K holds or not, for a particular value of y. In this way, we can find minimum value of y which satisfy the given property.
My views on 2nd part: If we further explore value of P like this:
- P = A * B * C
- P = A * B * (2^y)
- P/(AB) = 2^y // got stuck here
Here, at this step, I think if we apply log on both sides, something useful can come out. But, not able to solve it further. I'm not sure about this approach whether it is correct or not, but still tried hard to come up with the solution. But I couldn't solve. So, if possible, Please help me.
Anyone can suggest a solution for the same ? Any help will be appreciated. Thanks (in advance) for your time and support.











Assuming $$$y$$$ has to be an integer.
i) You don't need binary search. $$$y$$$ is $$$O(log(K))$$$ so all you need to do is just to increment until $$$P \geq K$$$.
ii) That said, applying binary search now (on appropriately small range) will give you $$$O(log(log K))$$$.
Our problem is to find the smallest integer $$$y$$$ that $$$3y(2y+1)2^y \geq K$$$. To get a grasp of how $$$y$$$ would look like mathematically, let's find the inverse of $$$x^2 2^x$$$. This turns out to be $$$\frac{2W(\frac{1}{2}\sqrt{x}\log 2)}{\log 2}$$$ for $$$x>0$$$, $$$W$$$ being the product log function (also known as the lambert W). Though I got this result from Wolfram Alpha, trying to derive this manually would be a great practice. Now let's plot this inverse function (which I will call $$$g(x)$$$) and $$$\log x$$$ on a graph. The result is as follows.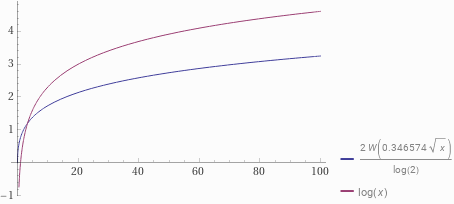
This gives us a convincing enough reason to assume that $$$g(K) \leq \log K$$$ for big enough $$$K$$$. Therefore, we can say that $$$g(K)=O(\log K)$$$. So searching linearly would clearly get you an $$$O(\log K)$$$ time complexity.
Now notice that the function $$$3y(2y+1)2^y$$$ is strictly increasing for all $$$y>0$$$ (as you already mentioned). Therefore we can binary search on the upper bound (approximated as $$$\log K$$$ above), and we get an $$$O(\log \log K)$$$ algorithm.