Банальная задача: Дано n точек на плоскости. Необходимо найти наибольшее количество точек, лежащих на одной прямой.
Вопрос: Решаема ли эта задача быстрее, чем за 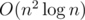 , или же О(n2) — с хеш-мэпом.
, или же О(n2) — с хеш-мэпом.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Банальная задача: Дано n точек на плоскости. Необходимо найти наибольшее количество точек, лежащих на одной прямой.
Вопрос: Решаема ли эта задача быстрее, чем за 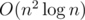 , или же О(n2) — с хеш-мэпом.
, или же О(n2) — с хеш-мэпом.
| Name |
|---|



There is problem called 3SUM, for which there are no known subquadratic (o(n2)) algorithms in common case. Many geometric problems are proven to be 3SUM-Hard, including "Given n points, check if there are 3 collinear points". Some more information in this paper.