402A - Орехи
Достаточно просто перебрать количество коробок, которыми мы воспользуемся. Предположим, это число равно ans. Тогда всего мы можем получить ровно cnt = ans + min((k - 1) * ans, B) отсеков. Если cnt * v ≥ a, тогда ответ равен ans.
402B - Деревья в ряду
Достаточно перебрать высоту первого дерева от 1 до 1000. При фиксированной высоте первого дерева высоты деревьев однозначно определены, то есть имеют вид: a, a + k, a + 2k и так далее. После этого необходимо подсчитать количество операций, чтобы получить красивый ряд из деревьев при фиксированной минимальной высоте. Обновим ответ. После этого выведем для самой оптимальной высоты все операции.
402C - Ищем граф / 403A - Ищем граф
Опишу два решения.
Первое. Рассмотрим все пары чисел (i, j) (1 ≤ i < j ≤ n). Выведем 2n + p пар в лексикографическом порядке.
Во-первых, понятно что достаточно доказать, что 0-интересный граф верный. Более того, достаточно показать, что - 3 интересный граф является верным. А как выглядит граф из первых 2n - 3 ребер. Очевидно, это граф имеет вид треугольников с общим ребром 1-2. Теперь предположим мы возьмем подмножество, которое не содержит вершины 1 и 2. Нетрудно увидеть, что в таких подграфах будет ноль ребер. Если в подмножестве ровно одна из вершин 1 или 2, то таких ребер будет k - 1, где k размер такого подграфа. Если две, то таких ребер 2 * (k — 2) + 1, где k размер подграфа.
Второе. Напишем перебор, который построит нам 0-интересные графы с количеством вершин 5, 6, 7, 8, 9. Теперь заметим, чтобы построить p-интерсный граф с n вершинами, достаточно построить 0-интересный граф, и потом в него p любых ребер, которых еще нет в графе. Как построить 0-интересный граф с n вершинами? Очень просто. Мы просто возьмем k несвязных компонент из построенных нами графов с вершинами от 5 по 9 так, чтобы суммарно в них было ровно n вершин.
402D - Улучшаем массив / 403B - Улучшаем массив
Опять опишу два решения.
Первое. Динамическое программирование. Подсчитаем динамическое программирование d[i][j] какое максимальный ответ мы можем получить, если перед нами сейчас префикс длины i и последний раз мы сокращали на gcd в позиции j. Понятно, что позиции следует перебирать в порядке убывания, как и размер префикса. Всего мы можем улучшить ответ в двух позициях в динамике из текущего состояния. А именно, d[i - 1][j] = max(d[i - 1][j], d[i][j]) — просто не будем сокращать на gcd текущий префикс. d[i - 1][i - 1] = max(d[i - 1][i - 1], d[i][j] + f(tgcd[j]) * i - f(tgcd[i - 1]) * i — выполним сокращение в текущей позиции. tgcd[i] — gcd всех чисел на префиксе длины i. Функция f(a) — возвращает красоту числа. Такую функцию просто реализовать за 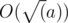 . Кроме того, можно ускорить работу этой функции, достаточно просто насчитать массив маленьких простых чисел. В таком решении очень важно не забыть, что каждый раз пересчитывать красоту чисел не нужно. Достаточно завести map < int, int > — который сохранит уже посчитанные значения. База динамики d[n][n] = curBeauty — текущая красота массива.
. Кроме того, можно ускорить работу этой функции, достаточно просто насчитать массив маленьких простых чисел. В таком решении очень важно не забыть, что каждый раз пересчитывать красоту чисел не нужно. Достаточно завести map < int, int > — который сохранит уже посчитанные значения. База динамики d[n][n] = curBeauty — текущая красота массива.
Второе. Жадность. Возьмем самую правую позицию, которая может улучшить ответ. Выберем эту позицию, и сократим в ней на gcd. Докажем, почему так делать верно. Пусть оптимальное решение (последовательность сокращений) имеет вид r1 > r2 > ... > rk. А мы построили решение l1 > l2 > ... > lm используя жадность. Понятно, то r1 ≤ l1, поскольку до этого позиции > l1 не могли ничего улучшить, ведь иначе наша жадность взяла бы их в качестве своего первого выбора. С другой стороны, r1 ≥ l1, ведь иначе мы можем взять и сократить в позиции l1 и только улучшить ответ, а это противоречило бы оптимальности решения ri. То есть, r1 = l1, а значит, мы можем воспользоваться нашими соображениями и далее, для больших индексов i.
402E - Строго положительная матрица / 403C - Строго положительная матрица
Будем смотреть на матрицу a как на матрицу смежности некоторого графа из n вершин. Причем, если aij > 0, значит мы имеем ориентированное ребро в графе между вершинами (i, j). Иначе, мы получим, что ориентированного ребра нет. Тогда, пусть b = ak. Тогда что обозначает bij? Верно, количество путей длины ровно k в нашем графе из вершины i в вершину j. Пусть pos такое, что a[pos][pos] > 0. То есть, у нас есть петля в графе. Значит, если из вершины pos достижимы все остальные вершины и наоборот, из всех остальных вершин достижима вершина pos, то тогда ответ YES, иначе ответ NO. Понятно, что если достижимость отсутствует, то понятно что для любого k akipos = 0. Если же достижимость имеется, то мы сможем добраться до петли, покрутиться некоторое количество раз в петле, а потом отправиться в нужную вершину.
403D - Красивые пары чисел
Во первых отметим, что на самом деле, длина последовательности не больше чем 50. Уже хорошо, а почему? Поскольку все числа bi - ai различны, то 0 + 1 + ... + 50 > 1000. Также представим, что мы имеем на самом деле последовательность попарно не пересекающихся отрезков, ci = bi - ai + 1 — длина отрезка. 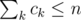 . Хорошо. Посчитаем динамическое программирование: d[i][j][k] — количество последовательностей из чисел c1 < c2 < ... < ci таких, что ci ≥ 1 и c1 + c2 + ... + ci = j и максимальное число в ней строго меньше чем k. Такая динамика поможет нам посчитать количество способов назначить длины отрезкам. Пересчитать такую динамику очень просто:
. Хорошо. Посчитаем динамическое программирование: d[i][j][k] — количество последовательностей из чисел c1 < c2 < ... < ci таких, что ci ≥ 1 и c1 + c2 + ... + ci = j и максимальное число в ней строго меньше чем k. Такая динамика поможет нам посчитать количество способов назначить длины отрезкам. Пересчитать такую динамику очень просто:
- база d[0][0][1] = 1,
- d[i][j][k + 1] = d[i][j][k + 1] + d[i][j][k] — просто увеличим верхнюю границу.
- d[i + 1][j + k][k + 1] = d[i + 1][j + k][k + 1] + d[i][j][k] — ставим текущую границу в последовательность, тем самым увеличиваем сумму и верхнюю границу.
Такую динамику нужно написать, используя O(N2) памяти, где N = 1000. После этого, умножим каждое d[i][j][k] на i!, поскольку мы располагать последовательность ci не в порядке возрастания. Таким образом мы умеем считать количество способов назначить длины отрезков.
Хорошо. Теперь как получить ответ для n, k? Пусть sum[len] = d[k][len][x], где x — некоторая верхняя граница. Очевидно, что нам дополнительно нужно еще раздать еще n - len единичек. С помощью этих единиц мы можем увеличивать расстояние между отрезками. Количество способов раздать эти единички равно числу C(n - len + k, k). Таким образом, для каждого n просуммируем по len полученные величины и сложим в ответ.
Также следует обратить внимание на то, массив C[n][k] должен быть достаточно большим и аккуратно расставить размерности.
403E - Два корневых дерева
Во-первых для каждой вершины первого и второго дерева подсчитаем две величины in[s], out[s] — время входа и время выхода из вершины в порядке обхода dfs из вершины 1. Теперь с каждому ребру из обоих деревьев мы сопоставим пару (p, q) — где p = min(in[u], in[v]), q = max(in[u], in[v]) где величины in, out для каждой вершины мы берем из дерева другого цвета. Теперь для каждой дерева мы построим два дерева отрезков (в сумме 4 дерева отрезков, да). В первом дереве отрезков мы будем пары хранить в следующем виде: мы будем хранить пару в вершине (вершина дерева отрезков это некоторый отрезок (l, r)) дерева отрезков тогда и только тогда, когда ее левая граница лежит внутри отрека (l, r). Аналогично, во втором дереве отрезков мы будем хранить пару в вершине (вершина дерева отрезков это некоторый отрезок (l, r)) дерева отрезков тогда и только тогда, когда ее правая граница лежит внутри отрека (l, r). Все пары в дереве отрезков мы будем хранить по возрастанию правой границы (левой во втором дереве). Такие деревья отрезков требуют 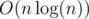 памяти, и построить можно за время
памяти, и построить можно за время 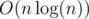 .
.
Хорошо. Как теперь ответить на запрос (l, r) — удалить ребра из дерева, такое что одна из вершин имеет время входа внутри (l, r) ? Будем спускаться по дереву отрезков. Предположим, мы сейчас находимся в некоторой его вершине. Поскольку в первом дереве мы храним все пары по возрастанию правой границы, то ответ на запрос, это некоторый суффикс массива его правый границы. После того, как мы обработаем эти ребра и начнем следующий этап, нам нужно модифицировать наше дерево. А именно, для каждой вершины дерева, в которой мы рассматривали суффиксы мы должны их удалить, иначе мы можем обработать их несколько раз. Таким образом, имеем решение за 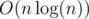 .
.
Авторское решение по Е: 6052738











Так и знал, когда писал такие решения, что у авторов, как и у меня, снова не хватит места на полях для поистине удивительного доказательства...)
Я несколько позже опубликую финальную версию разбора. Тем не менее, часто бывает полезно самому доказать решение, чем подсмотреть его в разборе.
А иногда бывает более полезно придумать решение самому, чем прочесть разбор. Но, тем не менее, это не причина для того, чтобы вообще не публиковать разборы.
Спасибо за интересный и оригинальный контест. Новый полезный опыт — из четырех отосланных задач для трех до конца контеста не иметь представления о том, почему отосланный код работает, в результате один код оказался нерабочим, и код по единственной задаче, в которой решение было понятно — тоже упал из-за баги, потому что в ней было целых 2 претеста, которые эту багу не отловили.
Вопросы, которые меня заинтересовали:
По С точно можно за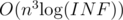 , где INF достаточно большое число. Быстрее способа я не знаю
, где INF достаточно большое число. Быстрее способа я не знаю
Можно даже ограничить INF сверху каким-то О(N^2), или это неправильно, и возможны случаи похуже?
Мне кажется, что O(n2) достаточно сомнительная оценка.
UPD. Хотя видимо я не прав, оценка верная. Понятно же, что в графе должен быть цикл, значит следует возвести матрицу в степень длины цикла. А потом можно воспользоваться решением за O(n2).
Чтож за контест такой "угадай, какое решение хотели авторы"?
Особенную изюминку добавляют КФ правила с тестированием после раунда.
Какой смысл для решения несет эта петля?
Если петли нету, то у нас нету "свободы действий". Например, может быть граф вида 1->2->3->4->...->n->1, в котором каждая вершина достижима из каждой, но длина пути между вершинами a и b не может быть произвольной.
Если петля есть, то мы можем получить путь любой достаточно большой длины, накрутив эту петлю нужное нам недостающее число раз.
Понятно, спасибо. Я как-то не учел, что все пути должны быть одинаковой длины.
не тупи больше)
А разве не правда то, что если у нас есть все n2 длин, то будет и все n2 путей длины НОК этих величин? Нас же в принципе интересует хоть какая-то одинаковая длина.
Думаю, нет. Контрпример — граф-линия, в котором из каждой вершины i (кроме 1 и n) есть двусторонние пути в (i — 1) и (i + 1). Тогда у соседних вершин будут только пути нечетной длины, а у вершин через одну будут пути только четной длины.
Да, согласен — не учёл, что необходимо возвращаться для повторения одного и того же пути.
сугубо психологический
After reading the tutorial my head started aching.
problem C is way easier than what they say, there is always a complete subgraph on the input (and it will always be i think, cause minimun number of edges is always 10 and vertex is always 5) so the 3rd condition (the tricky one) is always true, the other 2 conditions are met if you construct the graph with an O(N^2) algorithm. A good problem to think, but it is really easy to implement.
i tried implementing this approach during the contest, but got WA#3.
i think the reason is because for
n%5 != 0, u will have 2 or 3 extra edges to add. when these are added, it may result in the 2k + p condition being violated.weird, i got accepted in practice
По поводу задачи В:
В таком решении очень важно не забыть, что каждый раз пересчитывать красоту чисел не нужно — почему среди авторских тестов вообще нету таких, в которых это не работает (и не может работать)?
Мое решение 6056074 проходит системное тестирование за 30 мс.
При этом на тесте из 5000 больших различных простых чисел (для которых ничего запомнить не получится — они ведь различные) в запуске СF оно работает порядка 0.5 секунды. А если удариться об что-то головой и по непонятным соображениям написать все то же самое в long long — то 1.3 секунды, что явно TL. А на авторских тестах — летает.
В задаче div1 B лучше написать динамику где вторым параметром будет не позиция, а значения gcd. Ведь всего различных gcd будет не более log(10^9). Тогда и проблем с TL не будет.
Артур, на самом деле оказалось, что авторские тесты оказались слабыми, и не оказалось такого теста, где и такое решение может работать долго. Я добавлял тесты, когда готовил раунд, и все авторские решения работали достаточно быстро. На самом же деле, в тестах нет теста, где в первом массиве заданы различные большие простые. Тогда такое решение будет работать примерно 800 мс — 850 мс. Это моя вина, я уже понял и осознал свою ошибку.
тогда в качестве второго параметра будет выступать только 1, следовательно будет работать за N * sqrt(10^9)
Bdiv1 Можно поподробнее про вот эту формулу? d[i - 1][i - 1] = max(d[i - 1][i - 1], d[i][j] + f(tgcd[j]) * i - f(tgcd[i - 1]) * i)) (особенно интересует что такое tgsd)
tgcd[i] — gcd всех чисел префикса длины i
For Div2 Problem C, why do you say that it is enough to prove that a graph is 0-connected or -3-connected? Can you further explain?
Ok, first for each subset holds: number edges ≤ 2k - 3, so if we will add p + 3 edges, following will holds: ≤ 2k + p
not sure about this, but i think he means where did this "magic" number
-3come from?Some months ago I've read about Laman graphs. So, - 3-interesting graph is a Laman graph.
after just having read up on Laman graphs, i have to say their interest value seems much greater than
-3! :Dfor problem 402E, will you assign a_ij = 1 if a_ij > 0? Otherwise b_ij isn't the number of paths of length k from i to j
You can imagine, that there are aij edges from i to j.
nvm got it
For problem D,I think d[i][j][k + 1] = d[i][j][k] + d[i][j][k] should be d[i][j][k + 1] = d[i][j][k+1] + d[i][j][k]
Problem D,Div 1 d[i][j][k] i<=50,j<=1000,k<=1000 tried to write the solution described in the tutorial but ofc I got MLE(50*1000*1000),where is my mistake,I think the constraints I wrote are correct.
You can see, that there is only transitions from d[i][j][k] to
So, you for each step i + 1 you need only values from i. So, you can reduce used memory.
Yes that's the way I got accepted,but anyways just saying...
По задаче D div.1, почему количество способов добавить те единички равно именно C(n - len + k, k)? Как у нас отсекаются случаи, когда после добавления эти[ единичек, неравенства b1 < a2, b2 < a3...bk - 1 < ak ≤ bk не будут выполнятся.
For problem 403D could someone please tell me why the answer isn't sum[len] * ((k, n - len)) from Theorem 2?
Thank you!
On problem D div2, can i choose the same R multiple times ?
In problem c what is the meaning of p intersecting?
My solution for problem Div2 D is slightly different. Instead of updating all the indices, I just kept storing the last index which could improve the beauty. Take a look at my code for details. Please correct me if I am wrong. Could someone please explain to me why is my solution giving WA? http://mirror.codeforces.com/contest/402/submission/30985647 Thanks :)