Блог пользователя rembocoder

Сумма k-ых степеней первых n натуральных чисел – простой алгоритм
Автор rembocoder, история, 22 месяца назад, По-русски

Допустим, вы хотите для некоторых n и k найти сумму:

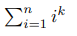
Вот известные формулы для первых нескольких k:

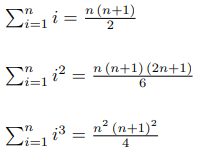
Допустим, вы забыли их. Что делать? К счастью, существует простой алгоритм для генерации этих формул.

Прежде всего докажем теорему.

Теорема

Предположим, что для каждого целого неотрицательного n:

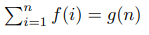
где f и g – многочлены. Тогда для некоторой константы c:

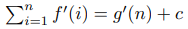
Доказательство

Для каждого целого положительного n верно:

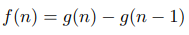
Эти два многочлена равны в бесконечном количестве точек, а значит, они тождествены. Что позволяет нам сказать:

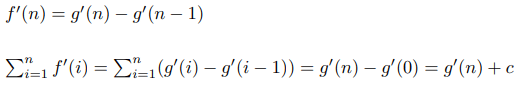
Применение

Допустим, мы хотим найти формулу для суммы квадратов. Тогда, используя нашу теорему, можно построить такой алгоритм:

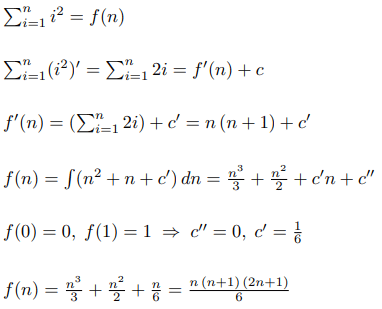
Теперь проделаем тот же алгоритм для суммы кубов:

  • Проголосовать: нравится
  • +87
  • Проголосовать: не нравится

»
22 месяца назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

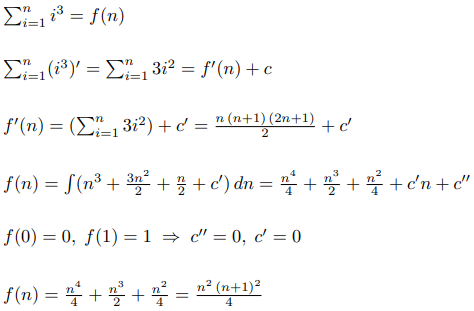
I hope the technique has already discussed in the very beginning chapter of Knuth's Concrete Math book.

→ Ответить
»
22 месяца назад, # |
← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

Hard version: 1677F - Tokitsukaze и драгоценные камни

→ Ответить
»
22 месяца назад, # |
← Rev. 2   Проголосовать: нравится +13 Проголосовать: не нравится

Maybe the easier and more direct way (if you want to do it for all $$$k$$$ up to some limit) would be to notice that

$$$ g_k(n) - g_{k}(n-1) = \sum\limits_{i=1}^n [i^k - (i-1)^k] = \sum\limits_{i=1}^n \sum\limits_{j=1}^{k} \binom{k}{j} (-1)^{j+1} i^{k-j} $$$

But on the other hand, it's also $$$g_k(n) - g_k(n-1) = n^k$$$, hence we get the recurrence

$$$ k g_{k-1}(n) = n^k + \sum\limits_{j=2}^k \binom{k}{j} (-1)^j g_{k-j}(n), $$$

or, for $$$g_k(n)$$$, it would be

$$$ g_k(n) = \frac{1}{k+1} \left[n^{k+1} + \sum\limits_{j=1}^{k} \binom{k+1}{j+1} (-1)^{j+1} g_{k-j}(n)\right] $$$

starting with $$$g_0(n) = n$$$.

Thus,

$$$\begin{gather} g_1(n) &=& \frac{1}{2} \left[n^2 + \binom{2}{2} g_0(n)\right] &=& \frac{n(n+1)}{2}, \\ g_2(n) &=& \frac{1}{3} \left[n^3 + \binom{3}{2} g_1(n) - \binom{3}{3} g_0(n)\right] &=& \frac{n(n+1)(2n+1)}{6}, \\ g_3(n) &=& \frac{1}{4} \left[n^4 + \binom{4}{2} g_2(n) - \binom{4}{3} g_1(n) + \binom{4}{4} g_0(n)\right] &=& \frac{n^2 (n+1)^2}{4}. \end{gather}$$$
→ Ответить
»
22 месяца назад, # |
← Rev. 2   Проголосовать: нравится +16 Проголосовать: не нравится

Also I think it would be nice to write down the algorithm from the blog in generic form for arbitrary $$$k$$$:

$$$\begin{gather} g_k(n) = \sum\limits_{t=1}^n t^k \\ g_k'(n) = c + \sum\limits_{t=1}^n k t^{k-1} = c + k g_{k-1}(n) \end{gather}$$$

From this, one gets

$$$ g_k(n) = cn + k \int g_{k-1}(n) dn, $$$

where $$$c$$$ is picked in a way that guarantees that $$$g_k(1) = 1$$$, that is

$$$ c = 1 - k \int g_{k-1}(n) dn \bigg|_{n=1}, $$$

and the free constant $$$c'$$$ that would appear from integration should be $$$c'=0$$$, as $$$g_k(0)=0$$$.

Compared to the scheme I described above, it's probably beneficial for larger $$$k$$$, as it allows to find it in $$$O(k)$$$ per term, rather than $$$O(k^2)$$$. I wonder if there is a more explicit formula for $$$c$$$...

→ Ответить