Всем привет! Меня всегда завораживало то, как хитро сплетены так называемые "строковые алгоритмы". Полгода назад я писал здесь статью о возможности быстрого перехода от Z-функции к префикс-функции и обратно. Некоторые опытные пользователи уже знают, что такие переходы возможны и между более сложными строковыми структурами — суффиксным деревом и суффиксным автоматом. Такой переход достаточно подробно описан на е-maxx.ru. Сейчас же я хотел бы в целом рассказать о такой структуре, как суффиксное дерево, а также поделиться достаточно простым (с теоретической точки зрения) способом его быстрого построения — получением суффиксного дерева из суффиксного массива.
Напомню, что суффиксное дерево — это бор, содержащий все суффиксы заданной строки. В самой простейшей реализации его построение потребует O(n2) времени и памяти — мы просто будем добавлять в бор все суффиксы по одному, пока не получим то, что получим. Чаще всего, такой расход времени и памяти оказывается слишком большим. Постараемся что-нибудь с этим сделать.
Для начала сведём ассимптотику по памяти до O(n). Для этого нам потребуется следующая идея: если мы имеем группу рёбер, которые соединены последовательно и не имеют ответвлений, мы можем объединить их в одно, которому в соответствие будет представлена подстрока, а не отдельный символ. Таким образом, мы получим сжатый бор (также известный как radix tree или patricia tree). Но это ещё не всё. Наконец, мы можем заметить, что нам незачем целиком хранить подстроку на ребре, мы можем хранить лишь индексы её начала и конца в исходной строке. Именно это и даст нам желанную линейную ассимптотику. Ведь действительно, вершины в нашем дереве теперь будут появляться только в местах разделения следующих друг за другом лексикографически суффиксах, а таких мест будет не больше, чем n - 1.
И, наконец, сведём к O(n) время построения дерева. Для этого нам подойдёт следующая стратегия:
1) Добавляем в бор лексикографически минимальный суффикс.
2) Для каждого следующего суффикса поднимаемся до точки lcp[i] и достраиваем его там.
Удивительно, но этого будет достаточно. Это связано с тем, что действия, которые мы совершаем на самом деле идентичны обходу дерева в глубину, который, очевидно, выполняется за O(n).
"Постой-ка, но ведь в заголовке написано о построении за O(nlogn), а у тебя тут сплошные O(n), что за подстава?"
Действительно, на самом деле, имея массив lcp суффиксное дерево УЖЕ можно строить за O(n). Однако всё ещё остаётся одна проблема — массив lcp тоже надо посчитать. И именно здесь нам на помощь приходит суффиксный массив, по которому уже в свою очередь можно получить lcp. Сравнительно простой метод его получения описан на сайте e-maxx.ru. Мы также можем использовать алгоритм Касаи для получения массива lcp за линейное время. Если скомбинировать его с каким-нибудь линейным алгоритмом получения суффиксного массива, можно будет свести время построения суффиксного дерева таким способом к линейной.
Достоинства такого способа построения суффиксного дерева:
- Просто для понимания.
- Приемлемый расход времени и памяти.
Недостатки:
- Алгоритм работает только в режиме оффлайн.
- Объём кода. Мне потребовалось почти 300 строк (100 из которых — на получение суфф. массива) и целый вечер на то, чтобы сделать что-то приемлемое по такой схеме. Я впервые работал с суффиксным деревом, поэтому не могу точно сказать, можно ли построить его таким алгоритмом меньшей ценой.
Здесь можно также ознакомиться с примером кода, который совершает все эти злодеяния для создания суффиксного дерева. Всем удачи и до новых встреч, надеюсь, статья окажется интересной :)
Для проверки корректности кода были использованы следующие задачи:
1393 — проверка корректности построения lcp.
1590 — проверка корректности построения непосредственно суффиксного дерева.











Долго не решался публиковать статью. Слишком трешовой лично мне казалась :)
Но всё же, опубликую. Посмотрим, что из этого выйдет.
@adamant:Very Nice Tutorial.If possible can you write the comments in English so that other users are able to understand
.
Наверное, это будет глупым выпросом, но что такое Sigma?
.
Ну, конкретно в моей реализации используется обычный вектор. Когда нам нужно добавить суффикс, мы в соответствующем месте делаем push_back, что, очевидно, работает за O(1). Да, запрос будет умножаться за логарифм, но не непосредственно построение. Но у меня-то и построение оффлайновое, наверное, в онлайне так сделать не удастся.
Кстати, unordered_map, ведь должен выдавать за O(1), не?
.
У меня поиск за O(|sigma|), но рёбра отсортированы лексикографически, так что можно бинарным поиском. Просто я добавляю суффиксы в лексикографическом порядке, а значит, когда я делаю push_back, этот суффикс гарантированно больше других уже добавленных.
unordered_map, кстати, 100%-ый, насколько мне известно. Там же, вроде, с коллизиями как-то борятся. Но, как мне тут подсказывают, у него O(1) только в среднем.
.
Здесь глупость, не читайте, плс
.
Только для так называемых целочисленных алфавитов: когда буквы являются целыми числами из отрезка [1, n]. Алгоритм Фараха (1997) для построения суффиксного дерева тоже работает за O(n) для целочисленных алфавитов.
.
А разве за n log n мы не используем цифровую сортировку?
А чем плох вариант по Укконену построить суфмас? Вроде там не используется факт про целочисленный алфавит.
Алгоритм Укконена использует факт про алфавит константного размера :) Для произвольных алфавитов у него , а про модификацию для целочисленных не слышал.
, а про модификацию для целочисленных не слышал.
Если речь о построении суффиксного массива за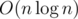 , то там идёт цифровая сортировка суффиксов, при которой на каждом шаге подсчётом сортируются классы соответствия. Т.к. классы соответствия всегда целые числа, мы можем только заменить сортировку единичных символов на первом шаге, и тогда получим алгоритм за
, то там идёт цифровая сортировка суффиксов, при которой на каждом шаге подсчётом сортируются классы соответствия. Т.к. классы соответствия всегда целые числа, мы можем только заменить сортировку единичных символов на первом шаге, и тогда получим алгоритм за 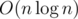 для произвольного алфавита.
для произвольного алфавита.
Если алфавит произвольный, то задачу сортировки можно свести к построению суффиксного дерева или массива. То есть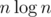 — нижняя граница.
— нижняя граница.
.
.
Да, надо бы поинтересоваться, что имеют ввиду авторы, говоря, что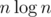 — "trivial lower bound") Алгоритмы, требующие целочисленный алфавит, тоже ведь сформулированы для RAM-модели. Может быть это нижняя граница для онлайновой задачи сортировки?
— "trivial lower bound") Алгоритмы, требующие целочисленный алфавит, тоже ведь сформулированы для RAM-модели. Может быть это нижняя граница для онлайновой задачи сортировки?
.
Нет, алгоритм Фараха не онлайновый.
Можно, за
O(N log^2 N). Статья, автор UrbanowiczКогда писалась эта статья, я был плохо знаком с публикациями по теме. На самом деле в 2005 году было показано, как это делать за : Amihood Amir, Tsvi Kopelowitz, Moshe Lewenstein, Noa Lewenstein "Towards Real-Time Suffix Tree Construction". В статье это называется BIS (balanced indexing structure) и отличие в том, что используют специальную структуру для определения порядка за константу (Sleator, Dietz "Two Algorithms for Maintaining Order in a List").
: Amihood Amir, Tsvi Kopelowitz, Moshe Lewenstein, Noa Lewenstein "Towards Real-Time Suffix Tree Construction". В статье это называется BIS (balanced indexing structure) и отличие в том, что используют специальную структуру для определения порядка за константу (Sleator, Dietz "Two Algorithms for Maintaining Order in a List").
сейчас еще поискал — вроде бы в этой статье (не нашел ее в открытом доступе) результат еще улучшили до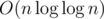
Только это не является построением суффиксного массива, по крайней мере прямым.
.
Там просто обычное дерево на алфавите константного размера. Алгоритм Вайнера в таких условиях сам по себе работает быстрее — за линию, обрабатывая очередной суффикс за амортизированную O(1). А в этой работе показано, как превратить амортизированную O(1) в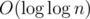 в худшем случае.
в худшем случае.
.
Бывает. Мне известны только две такие штуки: одна строит неполное суффиксное дерево, добавляя буквы в конце строки, другая — предназначена только для поиска всех вхождений. Обе с ограниченными приложениями. А для вариантов алгоритма Вайнера вроде как действительно нет.
There's also the possibility to build the suffix array in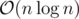 and then construct the suffix tree from that.
and then construct the suffix tree from that.
EDIT Nevermind, I see you are using that same idea already :) Although I don't see why you would need 100 LoC to implement suffix array + LCP in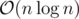 . Our implementation is a mere 24 lines, but it's
. Our implementation is a mere 24 lines, but it's 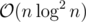 since it does not contain a linear time sort.
since it does not contain a linear time sort.
Your implementation has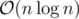 memory complexity in spite of my
memory complexity in spite of my 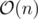 . But anyway, your way to calculate suffix array is kinda interesting, thanks a lot!
. But anyway, your way to calculate suffix array is kinda interesting, thanks a lot!
Ah, I see, yes that's a difference.
Isn't your suffix array build nlog2(n)? log(n) iteration in line 8 and nlog(n) for sorting in line 10. Correct me if i'm wrong.
Yes I changed the code in the meantime. It used to use LSB radix sort, but that seems slower in practice.
If you really need better performance than this, which sometimes becomes necessity, you can use the one that implements bucket sort. Otherwise yours is way better, both to understand and code.
Допустим я каким-то образом построил суффмассив, то как тогда искать lcp? Например в алгоритме с емакса используется дополнительный массив, полученный в ходе построения, но не сам суффмассив.
Построить массив lcp соседних суффиксов в суфмассиве, а потом lcp(i, j) = min(lcp[i], lcp[i + 1]..., lcp[j]). Массив lcp можно построить за линию алгоритмом Касаи.
Дерево-то мы строить можем, но вот где и как его можно использовать? Ответ на этот вопрос намного интереснее статьи о построении дерева.
Важный факт: суфдерево и суфмассив — вещи в подавляющем большинстве случаев взаимозаменяемые. В итоге, на контестах массив выигрывает у дерева за счет легкости написания как его самого, так и всякой обвески вроде деревьев отрезков.
В любом случае, построение суфдерева через суфмассив — это неплохое упражнение. Так что, ИМХО, наибольшая польза от этой статьи не для сообщества, а для Вас лично.
Пусть у Вас сохранится мотивация к саморазвитию :).
Ну, где и как его использовать, как мне показалось, уже и так достаточно хорошо освещено, а ничего о таком методе его получения лично я раньше ни разу не встречал. Возможно, я ещё расскажу об использовании дерева подробнее, если решусь таки когда-нибудь освоить алгоритм Укконена и написать об этом отдельную статью.
Кстати, меня вот недавно стал интересовать такой вопрос — а что вообще представляют собой задачи, которые решаются одной структурой, но не решаются другой?
Как то раз в Петрозаводске была задача (деталей не помню, могу где-нибудь соврать, если есть желание можете поискать — была год или два назад на контесте Zhukov_Dmitry) дана строка, нужно найти количество различных подстрок, таких что у них есть как минимум 3 непересекающихся вхождения в исходную строку. И решением было какой-то хитрый обход суффиксного дерева.
В дорешевание я сдал дерево, построенное по суфмассиву, но говорят, что в этой задаче можно было не строить дерево в явном виде, а делать тоже самое по суфмассиву, но я не понял как.
длина строки до миллиона?
не нашел контест с этой задачей, но вроде бы она легко решается.
построим суффиксный массив, массив LCP, и RMQ над LCP.
если подстрока (i, j) годится (т.е. у нее есть 3 непересекающихся вхождения), то (i, j - 1) тоже годится
если (i, j) не годится, то (i, j + 1) тоже не годится
далее пишем обычный алгоритм подсчета числа различных подстрок суффиксным массивом, для каждого суффикса максимальное j находим бинпоиском.
Да, немного наврал, нужно для каждой длины вывести отдельно.
Как я понял, ты предлагаешь для каждого i бинариком поискать наибольшее j, что у подстроки (i, j) будет 3 вхождения? Собственно сложность то в том, что не очевидно, как проверить есть ли три непересекающихся вхождения.
Problem G. 3-substrings
Petrozavodsk Summer Training Camp, Day 1 MIPT Contest, Friday, August 24, 2012
You are given a string S of length N. For each K = 1, 2, ... ,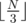 you should
find the number of different substrings of S of length exactly K such that each of them has at least three pairwise non-overlapping occurrences in S. (3 ≤ |S| ≤ 105)
you should
find the number of different substrings of S of length exactly K such that each of them has at least three pairwise non-overlapping occurrences in S. (3 ≤ |S| ≤ 105)
Пример:
Да, для заданных (i, j) можно за логарифм по RMQ над LCP найти границы подотрезка суфмассива, такие что LCP над всем отрезком будет >= j - i + 1. Да, можно найти минимум и максимум на этом же отрезка за еще один логарифм плюсом — соответственно самое первое вхождение нашей подстроки и последнее. Проверить, что эти вхождения не пересекаются. Но как понять что есть еще одно непересекающееся вхождение?
Можно персистентным деревом отрезков на найденном отрезке суфмассива узнать, есть ли там суффикс, имеющий длину из нужного диапазона.
Ага, можно и так
Мне вспомнилась одна притянутая за уши задача со сборов в Физтехе.
Задача: для заданной строки найти количество различных левых контекстов.
Определение левого контекста дам косвенно: две подстроки находятся в одном левом контексте тогда и только тогда, когда совпадают множества позиций вхождения их левых концов в исходную строку. Пример: строка
'abaa', левые контексты —[''],['a'],['aa'],['ab', 'aba', 'abaa'],['b', 'ba', 'baa'].Достаточно легко понять, что ответ на эту задачу равен суммарной степени вершин с исходящей степенью больше единицы (исключение: корень считаем в любом случае) в суфдереве, построенном по строке
S + (разделитель).Если же захочется решить эту задачу суфмассивом, то придется обходить неявно построенное суфдерево, хотя формально в решении будет фигурировать только массив.
А это не кол-во состояний в автомате для rev(S) ?
Очевидно, что оно самое (на контесте сдал именно это). Но здесь речь идет про дерево и массив, поэтому я решил не упоминать про автомат.
А не равно ли кол-во состояний в автомате для rev(S) кол-ву вершин в сжатом суфф дереве для S, раз уж на то пошло? Потому что если равно (а похоже на то), то его, судя по всему, можно найти таким образом:k + (|S| - T),
где k — различных элементов в массиве lcp, T — количество таких позиций i, для которых n - i, то есть, длина суффикса, присутствует в массиве lcp.
Обоснование: k — количество вершин во внутренней структуре дерева, (|S| - T) — количество листьев дерева.
А, нет, вру. Это в явном виде трудно записать. Но можно сделать так:
Изначально в ответе 1 (корень дерева). Идём в цикле по массиву lcp. Если lcp[i - 1]==n - pos[i - 1], то здесь мы достраиваем новый лист. Добавляем к ответу 1. В противном случае нам надо знать, встречали ли мы lcp[i - 1] ранее и если да, то были ли все lcp между текущей "встречей" и предыдущей больше, чем lcp[i - 1]. Если да, то вершина здесь уже есть, опять таки, добавляем лист в дерево, а к ответу — единичку. В противном случае прийдётся расщеплять ребро, добавляем 2.
В общем, это решение выглядит более правдоподобным, но оно, по сути, и есть обход неявного дерева.
А ещё, чтоб не извращаться с проверкой на минимум, можно при первой встрече (когда мы спускаемся по дереву) заносить lcp[i - 1] в стек, а когда будем подниматься, собственно, из стека доставать. Тогда нам будет достаточно проверить, является ли в данный момент число в вершине стека тем, которое мы хотим увидеть или нет.
I have a question.
I build Suffix array (SA) and longest common prefix array (LCP) of a string ending in #, now I proceed to create suffix tree.
I can separate SA in buckets for first character, then, for each bucket I can insert first suffix in the tree but when I try to insert second item, can I get the node where I have to put new item in O(1)? I can only think in binary search saving each instance to inserted nodes for each item.
Example:
assume we inserted suffixes 0, 1, 2, 3 now, when I have to insert sa[4], what is the best way for getting node x (see picture)?
I hope my question is clear, thanks.
You're such an artist X_X
I don't know exactly but it looks like you can't. But as I said in the entry, if you will just move up on tree every time, it will be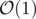 amortized because of its identity to dfs on tree. If you want to get moving to the next node non-amortized, you can keep for each node its ancestors that are pows of 2, i.e. 1, 2, 4, 8, 16, etc. Then you can get to the needed node in
amortized because of its identity to dfs on tree. If you want to get moving to the next node non-amortized, you can keep for each node its ancestors that are pows of 2, i.e. 1, 2, 4, 8, 16, etc. Then you can get to the needed node in 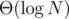 using this information.
using this information.
I'm writing my algorithm but I get struggle in that part.
What did you use in your implementation?
After adding some node to the tree I just move upward to the lcp[i] position and add next node there.
After lots of debugging, I finally get an implementation (java) that seems to work (at least with my tests).
But I can't pass TLE in this
I wonder if is possible to use this trick in java.
My suffix array is O(n log n)
Can you show your code?
link
It have comments.
Well, firstly I see that you always duplicate the node when inserting it. Maybe, you should do it only when you need (i.e. you shouldn't duplicate the node if it will be exact son). Also maybe you should try
map<char,int>to get O(nlogk) instead of O(nk)I just understood that my entry has no useful pictures. Well, if somebody is interested in them, here is picture, showing suffix tree of k790alex's string made via GraphViz. * after the string means that this node can be the last in some suffix.