I was wondering if there is any faster algorithm than O(N^2) that solves the following problem: Given a tree made of N nodes, where each node has an integer value asociated to it, find the minimum/maximum distance between two nodes whose values are coprime(if such a pair exists).
For example, given the following tree:
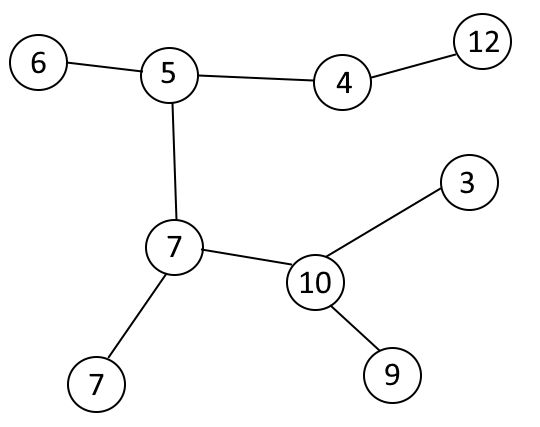
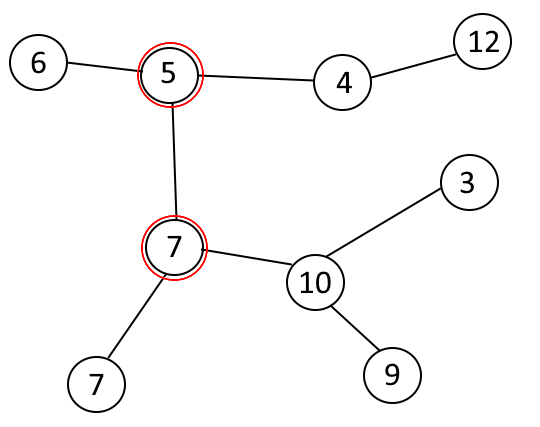
The minimum distance is 1 and can be obtained in multiple ways, but one of them is:
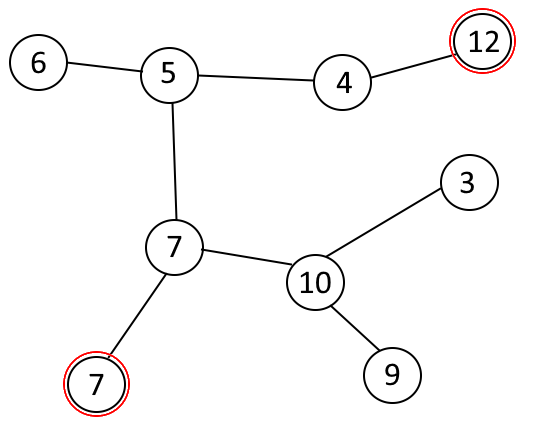
And the maximum distance is 4 and can be obtained like this:
I couldn't find anything like this by googling so I thought this is the best place to ask. Thank you in advance.
What's the constraint for ai
I didn't find this problem anywhere, just thought about it, I suppose you can make it
<=Nor<=1e6 or 1e7.Deleted.
It can be solved using centroid decomposition but I'm not aware of the details
why are you so sure that it can be solved with it?
How to use it here?
By using centroid decomposition you can turn the problem into finding $$$b_i = \max_{i\perp j} a_j$$$, which can be solved by using parallel binary search in
Unable to parse markup [type=CF_MATHJAX]
.The whole complexity is $$$O(n \log^2 n 2^{\omega(n)})$$$.How are you using parallel binary search if there are no queries ?
Each $$$b_i$$$ is a query.