Greedy

Consider the string $$$s=s_1,\dots,s_n$$$. Suppose $$$s_i$$$ is the first occurence of a letter $$$c$$$ (the string looks $$$s_1,\dots,s_i,\dots,s_n$$$). If we output $$$c$$$, the problem reduces to $$$s=s_{i+1},\dots,s_n$$$. The number of such outputs must be minimalized.

Observation: the largest $$$i$$$ we choose, the smallest string we obtain.

Greedy solution is always to take the largest $$$i$$$ such that $$$s_i$$$ is the first occurence. But after this traversal, the string we output is still a subsequence of $$$s$$$, so we need to output one more letter.

#include<bits/stdc++.h>
using namespace std;
int main()
{
    string s;cin>>s;
    map<char,bool>used;
    for(auto&c:s)
    {
        used[c]=1;
        if(used.size()==4)
        {
            cout<<c;
            used.clear();
        }
    }
    if(!used['A'])cout<<'A';
    else if(!used['C'])cout<<'C';
    else if(!used['G'])cout<<'G';
    else cout<<'T';
}

BFS

The number of permutations of the grid is $$$9!=362880$$$. We can precalculate the answer for each case.

Let's make a graph, where each vertex is a grid. And there will be an edge between vertices $$$A$$$ and $$$B$$$, if we can make one operation on $$$A$$$ and get $$$B$$$.

The answer for

is obviously $$$0$$$.

We can run BFS starting from this grid and get all the answers.

In practice, we can maintain each grid as an integer. For example the starting grid is $$$123456789$$$. Notice that we can still maintain the required operations using the integer.

#include<bits/stdc++.h>
using namespace std;
int pw[10];
int get(int x,int i)
{
    return x/pw[i]%10;
}
int f(int x,int i,int j)
{
    i=9-i,j=9-j;
    int di=get(x,i),dj=get(x,j);
    return x+pw[j]*(di-dj)+pw[i]*(dj-di);
}
int main()
{
    pw[0]=1;
    for(int i=1;i<10;i++)pw[i]=pw[i-1]*10;
    unordered_map<int,int>d;
    queue<int>q;
    q.push(123456789);
    d[123456789]=0;
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        for(int i=1;i<=8;i++)
        {
            if(i%3==0)continue;
            int y=f(x,i,i+1);
            if(d.find(y)==d.end())
            {
                d[y]=d[x]+1;
                q.push(y);
            }
        }
        for(int i=1;i<=6;i++)
        {
            int y=f(x,i,i+3);
            if(d.find(y)==d.end())
            {
                d[y]=d[x]+1;
                q.push(y);
            }
        }
    }
    int x=0;
    for(int i=8;i>=0;i--)
    {
        int a;cin>>a;
        x+=pw[i]*a;
    }
    cout<<d[x]<<"\n";
}

Tree theory

Let's define the Prüfer Code as $$$P=p_1,\dots,p_{n-2}$$$.

Feature of the Prüfer Code: if the given tree is $$$G$$$, and its Prüfer Code is $$$p_1,\dots,p_{n-2}$$$, after removing the leaf from $$$G$$$ with the smallest label, the code will be $$$p_2,\dots,p_{n-2}$$$.

That means, that after removing the leaf, we get the same problem with smaller Prüfer Code.

The integers that are missing in $$$P$$$ are leaves. Thats because the Prüfer Code is constructed is such a way, that it never contains the leaves of the tree.

Suppose we are proccessing $$$p_i$$$. There exist two cases:

1. We take the leaf with the smallest label that is connected with $$$p_i$$$ and delete the it.
2. We take the leaf with the smallest label that is connected with $$$p_i$$$ and delete the it. After what $$$p_i$$$ becomes a leaf.

In the second case $$$p_i$$$ becomes a leaf if $$$p_{i+1},\dots,p_{n-2}$$$ does not contain $$$p_i$$$. It follows from the feature.

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;cin>>n;
    vector<int>p(n-2),cnt(n+1);
    for(auto&x:p)
    {
        cin>>x;
        cnt[x]++;
    }
    set<int>leaves;
    for(int v=1;v<=n;v++)
    {
        if(cnt[v]==0)leaves.insert(v);
    }
    for(auto&x:p)
    {
        auto it=leaves.begin();
        cout<<*it<<' '<<x<<"\n";
        leaves.erase(it);
        if(--cnt[x]==0)leaves.insert(x);
    }
    cout<<*leaves.begin()<<' '<<*leaves.rbegin()<<"\n";
}

Graph theory

I assume, that if all the edges are directed from smaller vertex to largest one, the graph is acyclic.

Proof:

Suppose, such graph consists a cycle.

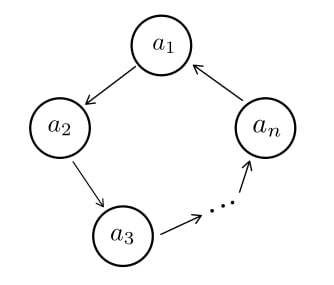
$$$a_1,\dots,a_n$$$ is a subset of vertices which forms a cycle.

$$$a_1 < a_2 < a_3< \dots <a_n < a_1$$$, because we construct the graph in such way. As you can notice, this expression is impossible.

#include<iostream>
using namespace std;
int main()
{
    int n,m;cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int u,v;cin>>u>>v;
        if(u>v)swap(u,v);
        cout<<u<<' '<<v<<"\n";
    }
}

Binary search

Let $$$F(k)$$$ is the amount of integers in the table with values $$$\le k$$$.

To calculate this function we can proccess each row seperately. $$$x$$$-th row contains integers $$$x,2x,\dots,nx$$$. There are $$$\min(n,\lfloor\frac{k}{x}\rfloor)$$$ integers from this list which are not greater than $$$k$$$.

To get the answer we need to find such maximal $$$k$$$, that $$$F(k)\le \lceil{\frac{n^2}{2}}\rceil$$$. Notice, the function is non-decreasing, hence we can use binary search.

#include<iostream>
typedef long long ll;
using namespace std;
ll n;
bool F(ll k)
{
    ll s=0;
    for(int x=1;x<=n;x++)s+=min(n,k/x);
    return s<n*n/2+1;
}
int main()
{
    cin>>n;
    ll l=1,r=n*n;
    while(r-l>1)
    {
        ll mid=(l+r)/2;
        if(F(mid))l=mid;
        else r=mid;
    }
    cout<<r<<"\n";
}

Monotonic stack

Let's fix the height of the rectangular. The high can be any of the boards, so let's consider $$$k_i (1\le i\le n)$$$.

The idea is that we can extend this rectangular to the left and right, while the heights are not less than $$$k_i$$$. Formally, the problem is to find:

1. The minimal $$$l$$$, that $$$1\le l\le i$$$ and $$$\min(k_l,\dots,k_i)\ge k_i$$$.
2. The maximal $$$r$$$, that $$$i\le r \le n$$$ and $$$\min(k_i,\dots,k_r)\ge k_i$$$.

If we found such $$$l,r$$$ for fixed $$$i$$$, the area of the rectangular is $$$k_i \cdot (r-l+1)$$$.

Let's maintain a stack which contains the positions $$$p_1,\dots,p_m$$$ such that $$$k_{p_1} \le \dots, \le k_{p_m}$$$. When we want to push $$$i$$$ to the stack, the condition of monotonic elements must be still met. So we need to pop the elements from the stack while $$$k_i \le k_{p_m}$$$. The advantage of such stack is that after erasing the positions, $$$k_{p_m}$$$ will always be the first element less than $$$k_i$$$. So the $$$l$$$ we need in the problem is $$$p_m+1$$$.

The idea of finding $$$r$$$ is symmetric.

#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int k[N],l[N],r[N];
int main()
{
    int n;cin>>n;
    for(int i=1;i<=n;i++)cin>>k[i];
    stack<int>s;
    for(int i=1;i<=n;i++)
    {
        while(!s.empty()&&k[s.top()]>=k[i])s.pop();
        if(s.empty())l[i]=1;
        else l[i]=s.top()+1;
        s.push(i);
    }
    while(!s.empty())s.pop();
    for(int i=n;i>=1;i--)
    {
        while(!s.empty()&&k[s.top()]>=k[i])s.pop();
        if(s.empty())r[i]=n;
        else r[i]=s.top()-1;
        s.push(i);
    }
    long long mx=0;
    for(int i=1;i<=n;i++)mx=max(mx,1ll*k[i]*(r[i]-l[i]+1));
    cout<<mx<<"\n";
}

Prefix sums

Suppose, the string contains the characters $$$c_1,c_2,\dots,c_k$$$. The first idea is to make $$$k$$$ prefix sums, where each of them responds for each character.

Now the substring $$$[l,r]$$$ is special iff $$$P_{r,ch}-P_{l-1,ch}$$$ is equal to $$$x$$$ where $$$ch$$$ is one of $$$c_1,\dots,c_k$$$.

Notice that if the string is special, than all the elements from $$$P_r$$$ are not less than $$$x$$$. So let's substract $$$x$$$ from $$$P_r$$$. The problem is, that we have no $$$x$$$, but we can substract the minimal value from $$$P_r$$$, bacause it is the largest $$$x$$$ we can choose.

The task is reduced to finding the number of such $$$1\le l\le r\le n$$$, that $$$P_r=P_{l-1}$$$, what can be done in $$$O(n\cdot k)$$$ time.

#include<bits/stdc++.h>
using namespace std;
int main()
{
    string s;cin>>s;
    map<char,int>h;
    int k=0;
    for(auto&c:s)
    {
        if(!h.count(c))h[c]=k++;
    }
    map<vector<int>,int>cnt;
    vector<int>P(k);
    cnt[P]=1;
    long long ans=0;
    for(auto&c:s)
    {
        P[h[c]]++;
        int mx=*max_element(P.begin(),P.end());
        for(auto&a:P)a-=mx;
        ans+=cnt[P]++;
    }
    cout<<ans<<"\n";
}

Trie, Bitmasks

At first, let's construct new array $$$a$$$ where $$$a_i=a_{i-1}\oplus x_i$$$. Now $$$x_l \oplus \dots \oplus x_r$$$ is equal to $$$a_r \oplus a_{l-1}$$$.

We can add the integers to a list and for each $$$a_r$$$ find optimal $$$a_{l-1}$$$. It can be done using Trie. It will contain integers in binary representation from the most significant bit.

Suppose we process $$$k$$$-th bit of $$$a_r$$$. If the trie contain the oposite bit from $$$k$$$-th, we can go to that subtree and improve the answer (because their xor gives $$$1$$$). Such improvement leads to correct answer because number comparison depends on the most significant bit.

#include<iostream>
using namespace std;
const int N=200005;
int T[N*30][2],t;
void upd(int x)
{
    for(int k=29,v=0;k>=0;k--)
    {
        bool c=(x>>k)&1;
        if(!T[v][c])T[v][c]=++t;
        v=T[v][c];
    }
}
int get(int x)
{
    int ans=0;
    for(int k=29,v=0;k>=0;k--)
    {
        bool c=(x>>k)&1;
        if(T[v][c^1])ans|=1<<k,v=T[v][c^1];
        else v=T[v][c];
    }
    return ans;
}
int main()
{
    int n;cin>>n;
    int x=0,mx=0;
    upd(x);
    for(int i=1,a;i<=n;i++)
    {
        cin>>a;
        x^=a;
        mx=max(mx,get(x));
        upd(x);
    }
    cout<<mx<<"\n";
}

Binary jumping

The greedy solution is to jump to the nearest end of the movie everytime while it possible. So let's generalize this idea.

Consider a function $$$up(k,i)$$$ returns the position $$$j$$$, when we do $$$2^k$$$ greedy jumps from position $$$i$$$.

The transitions are:

because the jump of length $$$2^k$$$ can be represented as two smaller jumps of length $$$2^{k-1}$$$.

To find the answer for a query $$$[l,r]$$$ we can start from the largest $$$k$$$ trying to make the longest jump and still be in the range. And if it is possible we perform this jump and add to the answer $$$2^k$$$.

In practice, it is better to do it backwards, jumping from $$$r$$$ to $$$l$$$. The problems are equal but the implementation is a bit easier.

#include<bits/stdc++.h>
using namespace std;
const int maxB=1000002;
int up[18][maxB];
int main()
{
    int n,q;cin>>n>>q;
    for(int i=0;i<n;i++)
    {
        int l,r;cin>>l>>r;
        up[0][r]=max(up[0][r],l);
    }
    for(int i=2;i<maxB;i++)
    {
        up[0][i]=max(up[0][i],up[0][i-1]);
    }
    for(int k=1;k<18;k++)
    {
        for(int i=1;i<maxB;i++)
        {
            up[k][i]=up[k-1][up[k-1][i]];
        }
    }
    while(q--)
    {
        int l,r;cin>>l>>r;
        int ans=0;
        for(int k=17;k>=0;k--)
        {
            if(up[k][r]>=l)
            {
                ans|=(1<<k);
                r=up[k][r];
            }
        }
        cout<<ans<<"\n";
    }
}

Bright mind

We trace the work of Euclid's algorithm for two coprime integers $$$a,b$$$

by writing '1' to a string if the second case and '0' in the third case. For example, for $$$a, b = 7, 5$$$, the string is $$$1001$$$. We denote this string by $$$trace(a,b)$$$.

Let us examine the construction of $$$trace(a,b)$$$ in terms of a number of distinct subsequences. By symmetry, we can only consider $$$cnt_1(trace(a,b)) = $$$ the number of distinct subsequences starting with $$$1$$$ (including empty string $$$\varnothing$$$) in $$$trace(a,b)$$$. We have

Taking $$$cnt_1(\varnothing)=cnt_0(\varnothing)=1$$$, we inductively obtain $$$cnt_1(trace(a,b))=a$$$ and $$$cnt_0(trace(a,b))=b$$$. So, the number of distinct subsequences in $$$trace(a,b)$$$ is $$$a+b-1$$$.

On the other hand, we can easily see that any binary string can be written via $$$trace(a,b)$$$ for some $$$a,b$$$ (just perform the algorithm backwards). Therefore, we have a bijection the set of binary strings with exactly $$$n$$$ subsequences (including the empty one) and the set of binary strings generated by $$$trace(a,b)$$$ for $$$a+b-1=n$$$.

The solution to the problem is easy now if one notices that we can iterate over the strings with exactly $$$n$$$ distinct subsequences. Go over $$$a$$$ and take $$$b=n-a+1$$$, then request $$$(a,b)=1$$$ and obtain $$$(a,n+1)=1$$$. In other words, the algorithm is the following.

1. Increment $$$n$$$ by 1 (to eliminate empty substring).
2. Iterate over $$$a$$$ coprime with $$$n+1$$$.
3. Take $$$b=n-a+1$$$ and relax $$$trace(a,b)$$$.

#include<bits/stdc++.h>
using namespace std;
string trace(int a,int b)
{
    if(a==b)return "";
    else if(a>b)return '1'+trace(a-b,b);
    else return '0'+trace(a,b-a);
}
int trace_len(int a,int b)
{
    if(a==b)return 0;
    else if(a>b)return 1+trace_len(a-b,b);
    else return 1+trace_len(a,b-a);
}
int main()
{
    int n;cin>>n;
    int b,mn=++n;
    for(int a=1;a<=n+1;a++)
    {
        if(__gcd(a,n+1)!=1)continue;
        int len=trace_len(a,n-a+1);
        if(len<mn)mn=len,b=n-a+1;
    }
    cout<<trace(n-b+1,b)<<"\n";
}

Greedy

See example 2 in.

FFT

First of all, we evaluate $$$p_n = $$$ the number of ones among $$$s_1, \dots, s_{n - 1}$$$ and $$$p_0 = 0$$$. Then, the naїve algorithm is the following:

1. iterate $$$i, j$$$ over $$$0, 1, 2, \dots, n$$$ and increment $$$cnt[p_i - p_j]$$$,
2. output $$$(cnt[0] - (n+1))/2$$$ (because we counted $$$i=j$$$ and $$$i\neq j$$$ twice) and $$$cnt[1], \dots, cnt[n]$$$.

The complexity of this algorithm is $$$O(n^2)$$$, which is not fast enough to solve the problem. Instead, we shall do the trick.

Consider the following expression

and it can be easily seen that the coefficient at $$$x^{k}$$$ is the number of pairs $$$(i, j)$$$ such that $$$p_i-p_j=k$$$, that is $$$cnt[k]$$$. As $$$p_n$$$ is the largest among $$$p_1,\dots,p_n$$$, we can make the second factor a polynomial multiplying the whole expression $$$P_{aux}$$$ by $$$x^{p_n}$$$

Then we multiply these two polynomials using FFT, and output the desired coefficients with respect to our shift by $$$x^{p_n}$$$.

#include<bits/stdc++.h>
using namespace std;
namespace FFT
{
    typedef complex<double>base;
    double PI=acos(-1);
    void fft(vector<base>&a,bool invert)
    {
        int n=a.size();
        for(int i=1,j=0;i<n;i++)
        {
            int bit=n>>1;
            for(;j>=bit;bit>>=1)j-=bit;
            j+=bit;
            if(i<j)swap(a[i],a[j]);
        }
        for(int len=2;len<=n;len<<=1)
        {
            double ang=2*PI/len*(invert?-1:1);
            base wlen(cos(ang),sin(ang));
            for(int i=0;i<n;i+=len)
            {
                base w(1);
                for(int j=0;j<len/2;j++)
                {
                    base u=a[i+j],v=a[i+j+len/2]*w;
                    a[i+j]=u+v;
                    a[i+j+len/2]=u-v;
                    w*=wlen;
                }
            }
        }
        if(invert)
        {
            for(int i=0;i<n;i++)a[i]/=n;
        }
    }
    vector<long long>multiply(vector<int>&a,vector<int>&b)
    {
        vector<base>fa(a.begin(),a.end()),fb(b.begin(),b.end());
        int n=1;
        while(n<max(a.size(),b.size()))n<<=1;
        n<<=1;
        fa.resize(n),fb.resize(n);
        fft(fa,0),fft(fb,0);
        for(int i=0;i<n;i++)fa[i]*=fb[i];
        fft(fa,1);
        vector<long long>res;
        res.resize(n);
        for(int i=0;i<n;i++)res[i]=(long long)(fa[i].real()+0.5);
        return res;
    }
};
int main()
{
    string s;cin>>s;
    int n=s.size();
    vector<int>p(n+1),a(n+1),b(n+1);
    for(int i=1;i<=n;i++)p[i]=p[i-1]+s[i-1]-'0';
    for(int i=0;i<=n;i++)a[p[i]]++;
    for(int i=0;i<=n;i++)b[p[n]-p[i]]++;
    auto Paux=FFT::multiply(a,b);
    cout<<(Paux[p[n]]-(n+1))/2<<' ';
    for(int i=p[n]+1;i<=p[n]+n;i++)cout<<Paux[i]<<' ';
}