I have been trying to solve this question.
After trying enough I read the tutorial but I am unable to understand it. I have attached the screen shot of the tutorial where I am facing problem below. 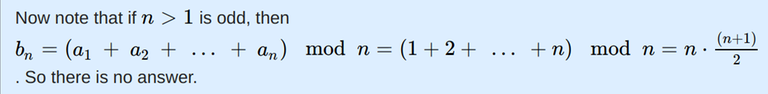 The tutorial says that for n>1 and n is odd, there exists no solution because, b_n = (a_1 + a_2 + ... + a_n)%n = (1+2+3+....+n)%n = (n*(n+1)/2)%n = 0 and b_1 is already 0, and there can't be two zeros in the array b. Hence, no solution for n>1 and n is odd.
The tutorial says that for n>1 and n is odd, there exists no solution because, b_n = (a_1 + a_2 + ... + a_n)%n = (1+2+3+....+n)%n = (n*(n+1)/2)%n = 0 and b_1 is already 0, and there can't be two zeros in the array b. Hence, no solution for n>1 and n is odd.
But, my doubt is that why can't I apply the same logic with n>1 and even, the same way I can prove that b_n = 0 and b_1 already 0. Hence, no solution for n>1 and n is even. Please correct me. Where am I understanding it wrong? I will be thankful for any help.











Try to plug an even $$$n$$$ (let's say $$$n = 10$$$) in the formula above.
Is $$$10 \cdot \frac{11}{2}$$$ a multiple of $$$10$$$? Why?
Because if $$$n$$$ is even, then $$$n$$$ in $$$\frac{n(n+1)}{2}$$$ would be reduced by the 2.
And also $$$n+1$$$ isn't divisible by 2, hence it cannot provide that extra 2. (Btw $$$n+1$$$ is not divisible by anything that divides $$$n$$$).
Hence all factors of $$$n$$$ except a 2, come from $$$\frac{n}{2}$$$ but that 2 can never be obtained. Hence it's not divisible.