This post is for those beginners who want to learn and practice matrix exponentiation. I am just here to share my idea on a very basic problem form lightoj(1142).
Task is simple A + A^2 + A^3 + ... + A^k =? where A is a n*n matrix.
- First time I thought ans will progress as geometric sum = (A*((A^k)-1))/A-1. or we can say... (A^(k+1) — A)/(A-1) where one is an Identity matrix. I was stuck in the matrix division portion for a long time. I don't know whether my geometric sum idea is right or wrong but i have another idea that can avoid that division.
- say A + A^2 + A^3 + ... + A^k = f(k)
- if(k is even,say k= 2x) we can write
- f(k=2x) = [A + A^2 + A^3 + ... + A^x ] + [A^(x+1) + A^(x+2) + .... + A^(x+x)]
- = [A + A^2 + A^3 + ... + A^x ] + [A^x(A + A^2 + A^3 + ... + A^x)]
- = [A + A^2 + A^3 + ... + A^x ] * (A^x + 1)
- = f(k/2) * (A^(k/2) + 1)
- else if K is odd we can write
- f(K)= [A + A^2 + A^3 + ... A^(k-1)] + A^k = f(k-1)+A^k
- very good problem for beginners. You can try if you have just started to learn matrix exponentiation.
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.11.2024 15:26:23 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Nice explanation. I think there is a typo in the else part, it should be odd rather than even.
yes, sorry and thanks :)
nice.
nice explanation.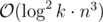 (where
(where 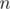 is the size of matrix
is the size of matrix 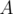 ).
).
complexity seems to be
I don't think so. Nobody can mutiply matrices in O(n2).
We can maintain needed powers of A, so complexity is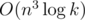
yeah thanks i mistyped initially. edited the comment now.
What about the correctness of this way, sum = (A^(k+1) — A)/(A-1) ? Is this method right? If it is right, we calculate in O((logk) * n^3).
Can't we write the recurrence as F(k)=A(1+A(A+A^2+...+A^k-1))=A(1+A*F(k-1))=(A^2)F(k-1)+A
great explanation thanks