Centroid Decomposition is kinda like Divide & Conquer on arrays (merge sort type divide&connquer) but for trees. Ever thought about it that way? Like HLD is a segment tree but for trees, what do you think? nvm just had a fun thought yesterday, never looked at it from this angle, cool (i attached some imagery) 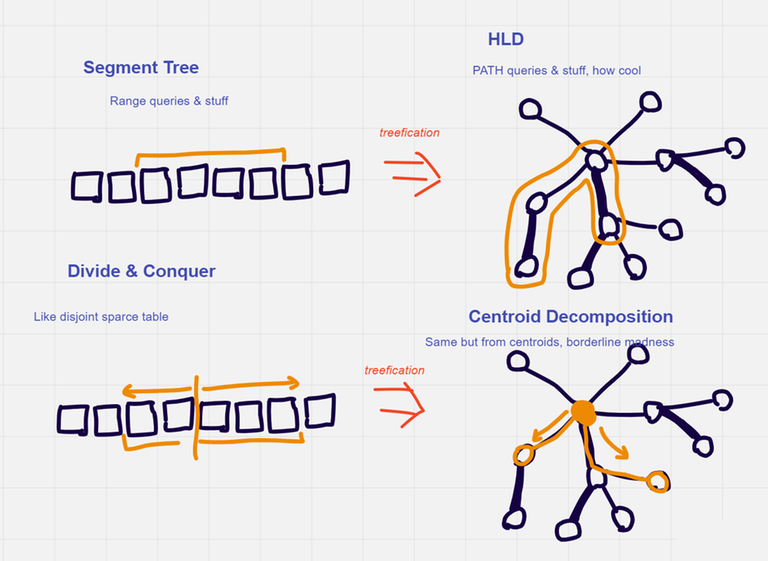
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
3 дня
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
3 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 20.11.2024 06:46:38 (k3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











There is more to say, but to begin with. When you need to solve problem on a tree, try solving it on array and then extend your methods to trees. You just showed examples of those extensions, which I use when facing tough problem sometimes.
True! Very common trick to solve tree probems, esp. query related, trees are dope
If I am not wrong then we also have: Fenwick Tree for Arrays = Binary Lifting for Trees
binary lifting on trees is more like sparse table on arrays actually, in my opinion
Hmm, that makes more sense
True! i guess you could also do disjoint sparse tables on trees with centroid decomposition if you can calculate LCA in O(1) (sparse table will do)
binary lifting on trees is more like binary search when implemented like this
https://mirror.codeforces.com/blog/entry/9901?#comment-177904
BITSET is kinda like BITSET on arrays but for trees
wow, it hits hard man
such ANIMAL...
Similarly, segment tree is persistent divide and conquer on an array.
Similarly, persistent segment tree is persistent persistent divide and conquer on an array.
Similarly, persistent n-dimensional (range sum) segment tree is (persistent divide and conquer on) $$$^{n-1}$$$ persistent persistent divide and conquer on an array.
Bonus points if this is done in a purely functional language just to add another level of persistence. More bonus points for a left-catenable/consible implementation.
"Binary Search Tree" is literally "binary search on array, but you store the entire recursion tree".
"Segment tree" is literally "divide and conquer, but you store the entire recursion history".
I wish people teach these kinds of things in classes. This is the definition of knowledge = connect the dots on information.
Koreans called this "divide and conquer on tree", before the word centroid decomposition became popular.