thanks for the second implementation it was a new and of course tricky implementation to me.:D

Well, imagine you an array [0..n - 1] and let us have an invariant: some function F which returns True for every a[i] as an argument for any i from [0..k] and False for every a[j] for j from [k + 1..n - 1]. Then my binary search which actually finds the border between these two parts of the array looks the following way:

l, r = -1, n
while r-l > 1:
    m = (l+r)//2
    if F(a[m]):
        l = m
    else:
        r = m

You can easily prove that l = k and r = k + 1 by the end of the while loop. In this case no worries about whether to increase m by 1 or not.

As an example this is the code which determines whether an element x exists in the sorted array [0..n-1]:

def BinarySearch(x):
    l, r = -1, n
    while r-l > 1:
        m = (l+r)//2
        if a[m] < x:
            l = m
        else:
            r = m
    return r != n and a[r] == x

As a suggestion, As we all know that Binary Search runs in O(logn) so implementing it recursive will not only be that bad in case of running time or memory, but also it can decrease the number of bugs you might have :)

And one other bug that anyone could have is stop condition of binary search. As a suggestion you can have a condition that when r-l<=2 check remaining items yourself. It can also decrease the number of bugs you might have.

And as the final word, bounds are very important in implementing binary search. Searching for the first occurrence, last one, or the one after last one,or etc. will require different bounds of passing middle point and left or right to the function.

Here is an example usage of Binary Search for Problem C,Round 218 : 5384392

P.S. Sorry for my bad english :)

Usually, when I have doubts about errors implementing binary search, which are common when I have to find things like "the largest element with this and that conditions..." (also lower_bound, upper_bound, etc), I do the following. I make the main loop of the binary search like this:

while (hi-lo > 5) { // here the usual binary search code }

and then, after that, a small linear loop for getting the correct result.

while (lo != hi) // increment or decrement hi or lo, respectively

The number 5 has nothing of special. It only ensures that the remaining interval is small enough. This avoids the possibility of errors on termination of the main loop of binary search, or the wrong choose of lo or hi. Although this approach is nice for saving you during a contest, it is not that good for understanding and proving correctness, which is fair more valuable IMHO.

I hope it was useful.

Let me try to generalize nhtrnm's answer a bit:

So far, every single time I used (integer) binary search, I could formulate the problem in one of two ways:

(1) Given a range of integers R = {l, l + 1, ..., r - 1, r} and a monotonically increasing predicate P, find the smallest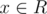 for which P(x) holds true. I then use the following code:

while (l < r) {
  int mid = (l + r) / 2;
  if (P(mid)) r = mid;
  else l = mid + 1;
} // after the loop, l = r = x

This might not work if P(r) = 0 (in this case the algorithm will return x = r), but you can easily extend your search range to r + 1 and artificially set P(r + 1) = 1 or you can just precheck for that situation.

(2) Given a range of integers R = {l, l + 1, ..., r - 1, r} and a monotonically decreasing predicate P, find the largest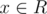 for which P(x) holds true. If we set Q(x) = !P(x), then Q is increasing and we can use (1) to find x + 1. We can also just use the following slightly modified variant:

while (l < r) {
  int mid = (l + r + 1) / 2;
  if (P(mid)) l = mid;
  else r = mid - 1;
} // after the loop, l = r = x

I find this approach so intuitive that I haven't done a single mistake while implementing binary search since.

In the case of finding the occurence of an element k in a sorted array, I would use variant (1) to find the first element i >= k and then check whether i = k. Note that in the case where k > x[n - 1] the algorithm still works because of the equality check at the end.

bool search(int x[], int n, int k) {
  int l = 0, r = n - 1;
  while (l < r) {
    int mid = (l + r) / 2;
    if (x[mid] >= k) r = mid; 
    else l = mid + 1;
  }
  return x[l] == k;
}

So, to summarize, you don't need to use this particular method, but you should have realized that there is really only one type of problem that can be solved with binary search and stick to only one particular implementation to solve this problem. You won't make a single mistake with binary search from there on.

i found a good binary search problem. and in my experience when you wanna minimize the maximum of something or maximize the minimum of something binary search is a good idea.

I lost track of how many problems I couldn't solve because of bad binary search implementations. Even this year during IOI I couldn't manage to solve completely one of the problems because my binary search had a bug that I wasn't able to find :(

if an array contains the following data: 1 2 3 4 4 4 4 4 4 6 7 8 Now I want to find the position of first occurance of data 4. How can I implement binary search for this problem? Here, the answer should be 3.

Generalized implementation of lower bound for non-decreasing func :

// result: min x of [firstX, lastX), when func[x] >= y
template<typename ArgType, typename ResultType, typename Func>
ArgType LowerBound(const ArgType& firstX, const ArgType& lastX, const ResultType& y, const Func& func)
{
  ArgType l = firstX;
  ArgType r = lastX;
  while (l < r)
  {
    const ArgType m = l + (r - l) / 2;
    if (func(m) < y)
      l = m + 1;
    else
      r = m;
  }
  return l;
}

Actually you don't need while in your second implementation. You can use just if, can't you?

I used to write binary search like this:

int binsearch(vector<int> & x, int k)
{
  int i = 0;
  for(int d = 1<<N; d; d /= 2)
    if(i + d < x.size() && x[i + d] <= k)
      i += d;
  return a;
}

I think this is more like Exponential search. It always performs at least as efficient as binary search.

This is simply awesome !

bool search(int x[], int n, int k) { int p = 0; for (int a = n; a >= 1; a /= 2) { while (p+a < n && x[p+a] <= k) p += a; } return x[p] == k; }

@pllk why do we need p=-1 in the count function while in search implementation p starts with 0.

In the second approach , It is more efficient if we take initial jump as a = n/ 2 instead a = n .

Great post, this will change the way I implement binary search in the future. Sometimes (interactive problems with limited number of queries) we want to use the minimum number of queries possible, and I thinking modify your code to do that gives an even prettier implementation, since it also gets rid of the inner while loop. Just fix one bit at a time starting from the leading bit of n (namely, $$$2^{\lfloor log2(n)\rfloor}$$$):

int p = 0;
for (int step = 1 << (int)log2(n); step; step /= 2) {
    if (condition(p + step)) {
        p += step;
    }
}