Блог пользователя redyellow

Binary search + hashing
Автор redyellow, 10 лет назад, По-английски

hey can you please list some easy string problems where we have to hash the strings and then use binary search on it. please give links to your solutions also because i am not able to implement it. thanks.

  • Проголосовать: нравится
  • +8
  • Проголосовать: не нравится

»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Here are a few problems on Topcoder that can be solved using binary search http://community.topcoder.com/stat?c=problem_statement&pm=3970&rd=7993 http://community.topcoder.com/stat?c=problem_statement&pm=3561&rd=6519 http://community.topcoder.com/stat?c=problem_statement&pm=4823&rd=8074 http://community.topcoder.com/stat?c=problem_statement&pm=4751&rd=8067

If there any problem in trying to solve it. Just say.

→ Ответить
  • »
    »
    10 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    thanks for those links but i actually meant problems on strings that involve hashing and then binary search. i have edited my question now. anyways i am solving these problems.

    → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
      ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

      Given a string, you need to find a longest palindrome substring. It can be solved in O(N) but try to solve it with hash + binary search in O(NlogN).

      UPD: I've found another problem. Click!

      → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
        ← Rev. 4   Проголосовать: нравится 0 Проголосовать: не нравится

        the second problem can also be solved in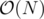 (without binary search or hashing). here is the solution.

        → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
        ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

        can you please check this code http://ideone.com/3tdMOZ for the second problem (codechef one).it uses binary search + hashing but i think its O(N^2*logN)

        EDIT: that code had a few bugs so this is my new code http://ideone.com/NIAIZf its still O(n^2logn)

        → Ответить
        • »
          »
          »
          »
          »
          10 лет назад, # ^ |
          ← Rev. 2   Проголосовать: нравится +3 Проголосовать: не нравится

          Well, the whole idea is right but your check function can be done much quicker -- in O(NlogN) instead of O(N2) and the resulting time will be O(Nlog2N).
          In your comment above you write:
          "for each substring of s2 of some length, we need to check if theres a similar substring in s1"
          I'm quite sure you can do it (maybe with some preprocessing) quicker than in O(N) for substring of s2.

          → Ответить
        • »
          »
          »
          »
          »
          10 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится

          Your check function works slow. How to check if there is a common substring of s1 and s2 which length is L?

          Let's put all hash-substrings of s1 which length is L into an array. This can be done in O(N). Then, for every hash-substring of s2 which length is L, check if there is a same hash in s1. We can just make a binsearch in our array of hashes. It will be O(NlogN).

          So, check will be in O(NlogN) + length binsearch in O(logN), overall O(Nlog^2N). Accepted :)

          Here is my solution: click. Instead binsearch, i've used unordered_set (IT MAKES PROGRAMM SLOWER), so it's better to write binary search.

          → Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

http://mirror.codeforces.com/problemset/tags/binary%20search?order=BY_SOLVED_DESC

→ Ответить