Задача A.
$$$a_2 - a_1 + a_3 - a_2 + \ldots + a_n - a_{n - 1} = a_n - a_1$$$. А значит нам нужно просто максимизировать это значение, а значит ответ максимальное число в массиве минус минимальное.
Задача B.
Давайте заметим, что каждая клетка задевает не более двух диагоналей, поэтому ответ на задачу хотя бы $$$\frac{k + 1}{2}$$$.
Утверждение: посмотрим на конструкцию, где мы в первой строке красим все клетки. А в последней все, кроме двух боковых. Тогда каждая такая клетка соответствует ровно двум диагоналям. И если $$$k \leq (2n - 2) * 2$$$, то ответ ровно $$$\frac{k + 1}{2}$$$.
Теперь заметим, что если у нас закрашены $$$2n - 1$$$ или же $$$2n$$$ клеток, то одна или две клетки соответсвенно будут соответствовать ровно одной диагонале, потому что в этом случае мы обязаны закрасить боковые клетки, ибо это единственные диагонали, которые мы не задели, а они уже покрываются другой диагональю, которой соответствует другая угловая клетка.
А значит ответ в случае $$$4n - 3$$$ такой же ввиду четности, а для $$$4n - 2$$$ это $$$\frac{k}{2} + 1$$$.
Задача C.
Давайте заметим, что условие, что мы можем получить сколь угодно большое значение означает, что нам необходимо получить гарантированно хотя бы $$$+1$$$ к нашим монетам. При первой же победе. В этом случае мы можем повторять данную стратегию бесконечно много раз.
Также заметим, что если мы до этого проиграли суммарно $$$z$$$, то в следующий раунд нам необходимо поставить $$$y$$$ такое, чтобы $$$y \cdot (k - 1) > z$$$, так как иначе казино может отдать нам победу. В этом случае условие на проигрыш не более $$$x$$$ раз подряд пропадет, а мы ушли в минус. А следовательно тактика является не оптимальной.
А значит решение — мы ставим сначала $$$1$$$, затем мы ставим минимальное число, чтобы победа перекрыла наш проигрыш. И если нам хватит на $$$x + 1$$$ то такую ставку, то казино обязано уйти в минус, иначе же мы не сможем победить.
И получается решение за $$$O(x)$$$, где мы просто циклом считаем эти значения.
Задача D.
Пусть $$$dp_v$$$ — это количество непустых множеств вершин в поддереве $$$v$$$ таких что, нет ни одной пары вершин в множестве, где одна вершина является предком другой.
Тогда $$$dp_v = (dp_{u_1} + 1) \cdot (dp_{u_2} + 1) \cdot \ldots \cdot (dp_{u_k} + 1)$$$, где $$$u_1, \ldots, u_k$$$ — это дети вершины $$$v$$$. Так как из каждого поддерева можно выбрать либо любое непустое множество, а также пустое. А выбор из каждого поддерева пустого множества означает, что выбрали единственную вершину $$$v$$$. (так как в нашей динамике не может быть пустого множества).
Теперь утверждение: ответ на задачу это $$$dp_1 + dp_2 + \ldots + dp_n + 1$$$. Так как если мы говорим, что пусть у нас есть пара вершин, где вершина $$$v$$$ является предком другой. Тогда ответ в этом случае это $$$dp_{u_1} + \ldots + dp_{u_k}$$$, так как мы можем выбрать ровно из одного поддерева такое множество вершин из динамики. (И как раз здесь мы используем непустые множества в состоянии динамики, ибо иначе учитывался вариант, где одна нет вершин, где одна предок другой). А $$$dp_1 + 1$$$ (где $$$1$$$ — это корень дерева) отвечает за варианты, где нет вершины, где одна вершина является предком другой.
Задача E.
Давайте для каждого ребра $$$i$$$ отметим множество пар $$$S_i$$$, которое оно перекрывает. Тогда утверждение: У нас различных множеств $$$O(k)$$$. Так как нас интересуют только ребра, которые находятся в сжатом дереве на этих $$$k$$$ пар вершин. А как известно, ребер в сжатом дереве $$$O(k)$$$.
Тогда нам нужно среди этих множеств выбрать минимальное количество такое, что каждая пара находится хотя бы в одном из них. А это делается динамикой по множествам следующим образом:
Пусть $$$dp[mask]$$$ — это минимальное количество ребер, которые нужно удалить, чтобы были в парах соответсвующим единичным битам из $$$mask$$$ было вычеркнуто хотя бы одно ребро.
Тогда пересчет следующий $$$dp[mask | S_i] = min(dp[mask | S_i], dp[mask] + 1)$$$ по всем различным множествам $$$S$$$, где $$$S_i$$$ это маска соответсвующая парам, которые проходят через ребро. А пересчет такой, так как мы к этой маске добавляем еще одно ребро.
В итоге получаем решение за $$$O(nk + 2^k k)$$$, где за $$$O(nk)$$$ мы для каждого ребра предпосчитываем множество пар, которое оно вычеркивает, а $$$O(2^k k)$$$ это пересчет динамики.
Задача F.
Давайте выпишем номера вершин в порядке их значений. Пусть это $$$v_1, \ldots, v_n$$$. Тогда должно выполняться $$$value_{v_i} \leq value_{v_{i + 1}}$$$.
Тогда у нас есть некоторые отрезки в этом порядке, для которых нам значения не известны. Тогда нам для каждого отрезка известно максимальное и минимальное значение, которое могут принимать значения на этом отрезке, пусть это $$$L$$$ и $$$R$$$. Тогда нам нужно для каждого числа на этом отрезке выбрать значение из отрезка $$$(L, R)$$$, чтобы сохранялся относительный порядок. А это известная задача и таких вариантов $$$\binom{R - L + len}{len}$$$, где $$$len$$$ это размер отрезка. А затем нужно перемножить все эти биноминальные коеффициенты.
Теперь заметим, что у нас $$$R - L + len$$$ большое, поэтому для подсчета можно просто воспользоваться формулой $$$\binom{n}{k} = \frac{n \cdot (n - 1) \cdot \ldots \cdot (n - k + 1)}{k!}$$$, так как сумма $$$len$$$ не превосходит $$$n$$$.










Problem C video solution with live coding: https://youtu.be/XRjHt1rnzqs
But it was taken off after the round, so it's fine.
Pathetic problem statement(s).
Is O(nklog²n) solution gives TLE for E??
Learn English
I have to admit C was really intuitive and fun though it could just be me but ABC were easier than usual.
D is also easy. simple multiplication, and one observation
Tbf you are an expert while ive been a pupil for less than 3 hour. The statement for D was really confusing.
Don't limit yourself to your levels.
Even being Pupil, you can solve 'D' or 'E' or 'F' . <3
Be LimitLess bro :) .
ATB , peace.
Thanks for this round! :)
for Problem C, Are these 2 conditions correct (t_i is amount bet in ith round):
(k — 1) * t_i > t_1 + ... + t_i-1 (if at any point we need to restart it covers for previous losses) for all i in 1 <= i <= x
k * (a — (t_1 + ... + t_x)) > a
We initially start with t_1 = 1
I am getting signed integer overlfow on my submission (not sure why) :
The 2 conditions are correct , though im not sure why got an integer overflow , your code is much more complicated than mine
k=2, k-1=1, sm=maxint, sm+1=overflow.
I should've submitted my solution in 128bit during the round.
for certain test cases the variable 'sm' can go beyond long long values, to fix just break the initial loop when sm > a
yes, this did the job.
wow,so good!
use
__int128@FairyWinx. please attache codes with comments
You forgot to translate the English title
...
Can someone tell me what I could do to make this submission pass (it works in C++ (https://mirror.codeforces.com/contest/1929/submission/246588961) but not in Python (https://mirror.codeforces.com/contest/1929/submission/246588699) nor does it with PyPy). I know C++ is better on codeforces but I'm just curious if there would be a way to make it work with Python.
Maybe instead of DFS implement it as a BFS. Accepted Python solutions do not use recursion.
Problems E and F are very good!
Can someone explain what the problem D was ?
https://mirror.codeforces.com/blog/entry/125851?#comment-1117492
Given a tree, you need to color each node in black or white. How many colorings exist such that the path between any two nodes contains atmost 2 black vertices
Can anyone explain the solution in terms of black and white?
I've talked about the black and white solution in detail here.
Here's a short summary:
In a tree, if you pick a set of vertices and they happen to be connected, we call it a connected induced subgraph. In this problem, let's focus on the subset containing all black vertices. How is this subset related to connected induced subgraph? If you think about it, these vertices represent the degree-1 vertices of a unique subgraph (and vice versa).
Hence, the problem asks you to compute the number of ways to select a subset such that the resulting subgraph is connected, which can be accomplished using simple DP.
Wow now I want someone to explain the statement of C and it's editorial XD
Very interesting math problem indeed!
In this problem, we need to check whether there exists a betting strategy for Sasha such that irrespective of the outcome of the rounds, Sasha still makes a positive profit. If the profit is positive for all outcomes, Sasha can keep using the same strategy over and over to make infinite profit.
Note that Sasha cannot lose more than $$$x$$$ times consecutively. Which means in the worst case he will lose $$$x$$$ rounds and win in the $$$(x + 1)^{th}$$$ round. Hence, we need to come up with a betting sequence of size $$$x + 1$$$ such that if Sasha wins at any point in the sequence, he makes a positive profit.
Once, he wins, he can restart over and use the same strategy again.
Also notice that we want the sum of this bet sequence to be as small as possible as we have only $$$a$$$ amount of money.
can you explain why case 3 3 6 is no ? still confuse ..
You might be thinking if you place 1 1 1 and lose then in next you can win, however the casino can let you win after 1 1. So you bet 3 and you got 3 so no profit.
but what if i both bet 2 for next 2 rounds , i'll definitely won't lose , or i just misunderstand the rule ....like sasha must gain more than he usd to have.o i think i got it , thanks
why should we check the sum of the previous terms over the x+1 terms should not be greater than "a" instead of x terms . In x+1th iteration will not it be a profit always?
No because on the x+1th iteration you must ensure that you have enough to bet to recoup all the losses of the previous x iterations and make a profit.
okay .. yes yes thank you i get it now
E and F were both Div2E-level according to the AC count and my impression. Don't be afraid to assign the same score to multiple problems next time. It makes the competition more strategic and fun (players can focus on their favorite topics).
I am really confused in problem C. Why can't we bet 1 coin every single time?? if we win, we keep getting k+1 more coins and in the worst case, even if we lose x number of times at any point of time, we only lose x coins. And once we lose x number of times, we can bet an amount such that we cover all the previous losses. If we use this strategy, we will always get more coins specially for the second last input given in the question (25, 69, 231). But the output for this input is NO. Where am i going wrong can anyone explain?
What if you don’t only lose but win sometimes when you bet 1. It resets the counter and you only get +2 ;)
But i am talking about the second last input given in the question. 25 69 231. Now, k = 25, x = 69 and a = 231. Now, whenever we win, we get a whopping 24 extra coins. But when we lose then even in the worst case, we lose 69 coins. Merely 3 wins will cover those many loses. So, it doesn't matter how the casino plays, i should always win as i always have extra coins. Even if i lose sometimes and not in a row, i only lose 1 coin per loss.
If you lose 30 times in a row and win once and lose 30 times in a row and win once, this 100 times in a row, what happens
Ohhh i got it now. Thankyou. Now that you pointed this out. i'm thinking how stupid i was to not consider this lmao
that's fine dude, happens haha; best of luck
for 3 3 6
He can lose 3 times by betting 1. Then he can bet 3 and his balance will become 9. So why is the answer given NO for it?
What if he loses 2 times and then wins when he bets 1. He’ll go back to initial balance. And he will never be able to make money!
then why 2 3 15 works??in works case he loses 2 times and then wins when he bets 1. He wont even go back to initial balance, his net profit will always be negative in worst case right? then why it says YES??
basically i need to know worst cases of both 3 3 6 & 2 3 15....
why would he bet 1 — there is a way to adjust bet size so that he can make infinite amount of money ;)
can you please explain me with example? a way to adjust bet size so that he can make infinite amount of money in case of 2 3 15? btw thanks for the help!
You could bet 1. IF you win, you get +1. You happy. IF you lose, you bet 2. If you win, you get 4 but you used 3. You get +1. You happy. IF you lose, you bet 4. If you win you get 8, but you used 7. You get +1. You happy. IF you lose, you bet 8 (you now have no money left) BUT you KNOW you will win and you will win 16, so you +1. You happy. You always end up +1 and with a big smile on your face.
dude for the first 10 minutes I also thought what you thought. I was like what the hell is happening? then later I had the same reaction as you did. how stupid I am.
yeah
In test case: 25 69 231
In the worst case, I would lose 69 times, but on 70th time if I bet 162 (cuz 231 — 69) then i would get 162*25 back, so total money in my pocket would be 3819, which is clearly more than 231, so why is the answer a NO?
That is because losing 69 times is not the worst case. If we choose to bet 1 coin until we continuously lose 69 times, casino will simply give us a win when we lose more than k. For example, we bet 1 everytime and lose 30 times consecutively. So, we lost 30 coins. But we bet 1 coin again and this time the casino gives us a win. So, we get 1*25=25 coins. We lose 30 and won 25. 30-25=5. We are still at a loss of 5 coins and now casino can again make us lose for 30 times as after winning the consecutive loss in a row count is reset. Everytime this happens, we lose 5 coins until we lose all our coins.
but he may be bet for 1 and win not loss so you have to check for each case
after 1 bet if may he win can he recover the total pay which is "0"
after 2 bets if may he win can he recover the total pay which is "0 + 1st bet"
....
after x bets if may he win can he recover the total pay which is "0 + 1st + .. + x-1 bet"
you can have a look on my submission => 246577540
upvote If it helps you plz
Yes, i understand now. Thank you.
but why for case 3 3 6 is No , still confused
if he bets for 1 coin and he loss, then he will need 1 coin to bet for the second time if he win so he gets 3 so his net win is 1 coin, now if he loss then he has to bet for 2 coins to get 6 and cover the total payed which is 1+1+2 then the net win is 2 coins, this is his last possible loss no it is graduated he will win so he has to bet for 3 coins to get 9 and cover the loss which is 1+1+2+3=7 then the net win is 2, if he make this he will get a net positive win in any case so he want minimum of 7 coins to make this sequence
got it , thanks a lot!
I u_nderstand you want to win a great victory in the x+1 times when you keep bet 1 coin every single time in the last x times.However,what if the casino let you win in the xth time when k=2 and x=10,and you had lost 8 coins already.Therefore,the tactic is not optimal._
How do you prove the conclusion for E?
Can you prove the claim you stated in E?
Edges in a compressed tree represent a set of edges in a path between vertices. You don't need to pick 2 edges from the same path since no new pathes would be locked
Can someone please give me a clear solution of problem C ... like I could not understand why at every step its mandatory to chose such a number which would nullify the previous losses ..
Notice that at every step (1 to x) you could lose or win. If you lose, money lost, just keep trying until x. But the tricky part is that if you win, as the result of that win, you need to have more maney than the amount you had initially.
Why? If the result gives you less or equal, this process could repeat forever and you would have less or equal amount of money, not achieving any value for $$$n$$$ (grater).
Having said that, if at some point you spent S, you would need to pay P, such that, $$$P * K + S > A$$$.
The smallest value of P to make sure you get more money at this point is $$$P = (A - S)/K + 1$$$.
Now your spent money S increase by P.
Don't spend more money that you had initially and the answer is YES.
Your explanation helped me finally understand C. Thanks a lot!
In test case: 25 69 231
In the worst case, I would lose 69 times, but on 70th time if I bet 162 (cuz 231 — 69) then i would get 162*25 back, so total money in my pocket would be 3819, which is clearly more than 231, so why is the answer a NO?
cause there's no rule saying that casino can't let you win before that. say you bet 1 1 1 1 1 1 and win on the 69th time, then you can lose on your 70th when you bet 162. you lose your guarantee if you win any round before that
LONG EXPLANATION from what i have understood,the casino always tries to make us loose coins and play optimally.Therefore,if we dont play according to the cases in which we can win at any point within the x times of betting(i.e not necessarily winning after x times but before that),we will loose some money(because we will be betting only 1 coin greedily and thus winning only k coins when we win after x turns and spending x coins),but we want to increase our coins once we win any bet(before x turns),therfore our each bet should be fixed and according to the condition of making profit. we are taking different scenario in which casino can play because casino doesnt play in fixed order,so we need to be in profit whenever there is a win before x turns,else we will only bet 1 coin greedily knowing its a loss,but if it would be a win,we will win only k coins which may or may not result in overall net profit
i get that if its a win and the won coins by the chosen number of coins y nullify the previous losses , it will be a win ... but what if the condition is a loss ?
Then won't it be more optimal to chose 1 there instead of such a y ?
thats what i am talking about,if u play thinking like what if i bet y coins and loose then why not bet 1 instead,but casino being the decider of win/loss will give u win if u choose 1 and your profit will be minimal.A better way to approach how and what amount to bet is to think that no matter what the result will be (i.e whether win/loss) i should have profit after the case of first win,in this way you will be optimising your approach by winning whenever their is first win and not just minimising the coins lost in loss bet just a conclusion,dont play like," i should bet 1 coin because what if its a loss",instead play like " i should bet y and be in profit if its a winning round"
do u think the near about 7k people who solved the problem in the contest might've thought about it this deeply ? Honestly , I found this C as one of the hardest C's ever as I couldn't even decide what an optimal strategy would be .... thanks for the explanation btw :)
yeah,even idk how there are so many submissions on this c,maybe others have thought of some easier approach to this question.
Upd: understood now
Why? I think it’s easy to read. Maybe you should improve your English.
Definitely not easy to read. My English is just fine; I've lived in the UK for a long time now.
I am confused on Problem E. Could anyone prove that "we will have total $$$O(k)$$$ different sets?". When I was thinking it, I thought the total of sets is $$$O(2^k)$$$. Now I think it is lower than $$$O(2^k)$$$, but I can't understand why it will reduce to $$$O(k)$$$. Thanks.
I have an idea of proof. First, let's take one simple path, imagine that it looks like an interval. Let's add more simple paths. What happens if we add new intervals? We see that the new interval divides 2 intervals into 2 others. I'm not the best artist, but I hope that everything will become clearer with the drawing.
https://imgur.com/a/tF4H1Cu
Thank you.
In problem E, "precomputing the set of pairs removed by each edge for each edge" could be done in $$$O(n + k)$$$.
A path covers an edge if and only if the two ends of the path ($$$a_i, b_i$$$) is on different sides of this edge, where each side is a subtree. Let's focus on one of the two sides. Each time a traversal of a subtree is finished, find that set of this subtree. The set belongs to exactly an edge, except the whole tree.
Details are in submission 246548785.
Sorry, but what's the meaning of "The set belongs to exactly an edge, except the whole tree."?
For example, the special edge change from $$$(x,y)$$$ to $$$(y,z)$$$. The edges from $$$y$$$, and not connect with $$$x$$$ or $$$z$$$, symbol a subtree that changed the direction of this change. That means, $$$y$$$, and some of subtrees, from left of the special edge to the right side.
I can observe the change of it is variously, so I infer the amount of possible sets will be $$$O(2^k)$$$. But I couldn't draw a tree with $$$7$$$ possible nonempty sets with $$$3$$$ colors.
So, could you explain why the amount of the possible sets will be $$$O(k)$$$?
Thank you.
Sorry for my being poor at English. I'm afraid I still couldn't make it clear, so I recommend to read the code for better understanding.
That sentence should be "The set of a subtree belongs to exactly an edge, except the set of the whole tree". More precisely, let $$$v$$$ be the root of a subtree when doing dfs, $$$u$$$ be the parent node of $$$v$$$, then $$$(u, v)$$$ is that edge.
As for the reason why the amount of the possible sets will be $$$O(k)$$$, there's a proof written by YocyCraft.
I hope this can help you.
Thank you.
fast Editorial
I'm sorry that I can't understand why in D, we need to sum up dp[] and that is the ans."as we can select such a set of vertices exactly from one subtree from the dynamic programming states" is hard for me to understand, can anyone tell me why?
In my opinion, the answer can be divied into two situations.
There is no pair that one vertex u is the ancestor of another vertex v. To calculate this part, just use dp as the solution did. And the answer of this part is dp_1(1 is the root) + 1.
The another situation is that there exists at least one pair that u is the ancestor of v. As we already know, the answer of this part is dp_2 + dp_3 + ... + dp_n. As we consider every vertex from top to bottom, if we choose 1 to be the ancestor, the contribution of this will be dp_2 + dp_3 + ... + dp_k (assuming that 2,3,..,k are children of 1); then we consider choose vertex 2, the contribution of this will be dp_5 + dp_6 + ... (assuming that 5,6,... are children of 2); and so on. In the end, the total answer of this part is exactly dp_2 + dp_3 + ... + dp_n.
Can D problem be solved by using combinatorics, inclusion-exclusion principle and rerooting.
Like by at each root, calculating how much be the total number of good sets, where this root is always a part. Like, we could easy calculate this number using combinatorics and the number of leafs in the subtree of direct children of root.
But there would be extra contribution by each root, like 3-member set would be added thrice, each when considering each part of this set as root.
Could someone explain if they did it this way?
I thought about this, but we cannot leave the subtree as a black box, because the number of vertices we can include in the set depends heavily on the structure.
As an extreme example, if one child subtree is simply a long path of $$$k$$$ vertices, then only one vertex in this path can be included in the good set (assuming the root is also included). On the other hand, if a child subtree is a star, i.e., a single vertex with $$$k - 1$$$ leaf children, then all $$$k - 1$$$ of these leaves can be included in a single good set (which also includes the root), so any subset of those leaves can be included as well.
Therefore, counting the number of good sets would require exploring the subtree, and if we were to adjust the strategy and refine it further, it would eventually lead to tree DP, as opposed to a pure combinatorics approach.
Actually we can leave the subtree as a black-box,
and just store the number of leafs in the subtree,
UPDATED
Just count good sets consisting of 2, 1 or empty node separately, that would be n+1+(nC2) (number of nodes+empty set+ taking 2 nodes at a time),
then for the root's every direct children i's subtree, let num[i] be number of leafs in that subree node node i,
we add in the answer+= (2^(num[i])-1)-(C(num[i],1)); (for counting sets of size greater than two)
because taking leafs(and considering them as part of good set) from different direct children will make the bad intersections 3, in path among these three vertices only.
And we can easily reroot the number of leafs in direct children.
There would be just problem of over-counting which I was thinking to solve with inclusion-exclusion but couldn't so asking
For example , taking sample testcase
3->4, 3->2, 3->1
let ans=0
considering nodes of size 1,2,or 0 = 4+6+1=11
taking 3 as root, considering every direct child contribution in good set of size 3 = 3* (2^1-1)-C(1,1)
taking 4 as root, considering every direct child contribution in good set of size 3 = (2^2-1)-C(2,1)=3-2=1
taking 2 as root, considering every direct child contribution in good set of size 3 = (2^2-1)-C(2,1)=3-2=1
taking 1 as root, considering every direct child contribution in good set of size 3 = (2^2-1)-C(2,1)=3-2=1
but 3-sized sets contribution will be overcounted thrice, so actual contribution of 3-sized sets= (0+1+1+1)/3=1
so total ans+=1, which is ans=11+1= 12
I don't think number of leaves would suffice to characterize the subtree. For example, suppose a subtree has four vertices and two leaves. Then some of the possible scenarios include:
1) subtree root has one child, which has two leaf children. Considering all subsets of the leaves gives us 4 sets that you accounted for, but there are also two more: the set with only the subtree root and the set with only the child of the subtree root, so there are six in total.
2) subtree root has two children, one of which is a leaf while the other has a leaf child. Again, the subsets of the leaves give us 4 sets, but now there are three more: the set with only the subtree root, the set with only the non-leaf child of the subtree root, and the set with both children of the subtree root.
Unless I'm misunderstanding how you're counting the sets, it seems 2^{number of leaves} is insufficient, and the actual number can be different even for the same number of vertices with the same number of leaves.
Actually it seems to suffice to chracterize the subtree in this case.
If you look at the explanation I gave above,
I counted vertex sets of size 0,1,2 separately, which would allow me to handle all the cases.
Like your example
1) total sets = empty set + (1-cardinality set) + (2 cardinality set) + (**3+** cardinality set )
Note 3+ cardinality set is calculated by considering the leafs in the subtree of direct children of root, not by associating or taking any two vertices from different direct children at the same time because 3 vertices will be bad in a path which we don't want
current ans= 1 + 4 + C(4,2) + (3+ cardinality sets)
for first case structure
for current root, 3+ cardinality sets will be (2^2-1)-(2)= 1
for second case structure
for current root 3+ sets will be = (2^1-1)-1 + (2^1-1)-1 = 0 ,
becuase every possible thing has already accoounted for, and now if I do re-rooting and removing over-countings, i would get the current answer.
Taking direct children subtree leafs separately will always give the correct answer
In the Image, first image is second case and vice-versa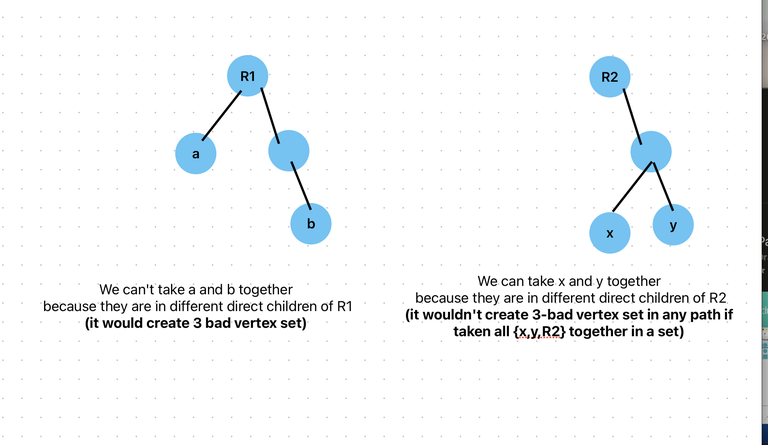
I was trying to find a solution using combinatorics as well however this leaf counting approach run into a problem of not being able to count number of leaves which can be included in a good set containing two internal nodes. Example consider the test case
2-1, 1-3, 4-1, 2-5, 6-3,
Couldn't figure out how to count the set {2, 3, 4} which contains two internal nodes and one leaf node.
Yeah this thing and case, broke my approach and combinatorial intuition, would need to think more if it can be done in pure combinatorial way
I still dont know what does 1929C - Sasha and the Casino mean.I was stuck in it.
Problems in this round are pretty good. I stuck in problem c for long time and problem B accepted is just a fluke.
Simple Round, AK in 1:07
I solved the problem $$$E$$$ with $$$FWT,O(nk+2^kk)$$$,amazing! here
what is FWT?
Fast Welsh Hadamard Transform, also known as XOR Convolution.
Define the convolution of $$$f(x) = \sum\limits_{i=0}^{2^n-1} a_i x^i$$$ and $$$g(x)= \sum\limits_{i=0}^{2^n-1} b_i x^i$$$ is $$$h(x)= \sum\limits_{i=0}^{2^n-1} c_i x^i$$$,subjecting to $$$c_k = \sum\limits_{i \oplus j=k} a_ib_j$$$,where $$$\oplus$$$ is any of the bitwise operations. The role of the $$$FWT$$$ is to quickly compute $$$h(x)$$$.
How to solve it using FWT?
Discover which paths each edge can be on using $$$dfs$$$. By state compression, define $$$f_i$$$ to mean whether there exists an edge that lies on all paths in state $$$i$$$. Using "OR convolution", the answer is the smallest $$$c,[x^{2^k-1}](f(x))^c > 0$$$
thanks!
I only can solve it with $$$O(n+2^kk\log n)$$$. Could you describe the further detail of your code?
I think we're thinking along the same lines, except that I've made an optimization to it.
When calculating $$$f(x)^c$$$, I don't bother to reduce $$$f(x)^c$$$ with an inverse transformation, but instead I just calculate $$$[x^{2^k-1}]f(x)^c$$$.
how to calculate $$$[x^{2^k-1}]f(x)^c$$$ ? The essence of OR convolution is to compute the sum of subset weights, $$$[x^i]F(A(x)) = \sum\limits_{j \subseteq i} [x^j]A(x)$$$. So the inverse transformation is $$$[x^i]F(A(x)) = \sum\limits_{j \subseteq i} (-1)^{popcount(i-j) \bmod 2} [x^j]A(x)$$$ through inclusion-exclusion principle.
So each time $$$f(x)^{i-1}*f(x)$$$ can do $$$O(2^k)$$$ instead of $$$O(2^kk)$$$
I understand, it's artful.
Thank you.
E was stunning
An error. The spoiler name of Problem F is wrong. It should be "solution" instead of "soloution".
@FairyWinx Please fix this.
It's not problem
C is crazy
agree
The contest was so cool and awesome!
The contest was so cool and awesome!
Maybe I misunderstand the problem D. Can someone correct for me, I think the problem said: "Find all set of vertices such that no 3 vertices are connected", is it right?
Upd: Nevermind, i really misunderstand :((
For example, we select a set of vertices and assume all of them are dangerous. If we are able to find a simple path (we can't visit the same vertex again) that connects the set of vertices, such that the path contains 3 or more vertices that are dangerous, then we remove it from our result.
In other words, if we connect two vertices from that set through a simple path and any other dangerous vertex lies on that path, then that set is removed.
For instance, in the second test case, we didn't remove {1, 2, 4} because there is no simple path that can cover all three of them. But in the case of {2, 3, 4}, we have a simple path.
I still cannot get the idea of problem C, can someone please explain it for me in detail? I don't understand the part that "we bet 1 at first, then we bet the minimum number such that the win covers our loss". Or if you have a more understandable solution, please tell me (it's ok if it consume more time to execute). Thanks a lot.
Basically, to find the answer you should just simulate the first x rounds and determine whether the initial number of coins increases or decreases. How can you do that? Every round Sasha should make a bet. Suppose he lost i-rounds in total, let's define it as y. To recover from all of these losses his next bet must follow this inequality: bet * (k — 1) > y; bet > y / (k — 1); bet = 1 + y / (k — 1). Now, all you have to do is check whether his current bet doesn't exceed the money he has after i loses.
Here is a sample solution: https://pastebin.com/3KQfVHaZ
You are so kind and dedicated, I read your previous comment and intended to send you a reply but you deleted it, LOL. You added a sample solution, I appreciate it. Once again thanks for your help.
I think you should use YocyCraft's explanation for problem C.
Thanks
problem c was literally great , don't know why I couldn't solved it during the contest. Tried just now and actually solved it , don't know why this is happening since last few contests, my rank is going down and down :( .
in problem B , the second testcase while we need 3 diagonals why dont we colour the corner cell? It will take 3 diagonals.
it doesn't? corner cells only take 2 diagonals.
[1][1] , [1][1] : [2][2] and [1][1] : [3][3] , sorry if i have any misunderstanding
can you visualize it lol cuz i kinda don't understand
they all count as the yellow one
oh , tysm
here you go, 2 diagonals
Почему в случае "3 3 6" ответ "Нет"? Может кто-то найдет ошибку в моей логике, но смотрите. Саша знает, что он может проиграть не более X раз подряд, стало быть он точно знает, что если он уже проиграл X раз подряд, то следующая ставка будет ТОЧНО выигрышной. Тогда давайте ставить 1 монетку всегда, кроме того случая, когда игра ТОЧНО выигрышная, будем обозначать П — проигрыш, а В — выигрыш. Рассмотрим 2 случая, когда Саша проиграл X подряд и X+1 раз будет точно выигрышным, и случай когда ТОЧНО выигрышных ситуаций нет. Пусть у нас идет последовательность ПППВ, мы проиграли 3 подряд, значит следующая игра выигрышная, значит Саша может ставить на нее все деньги. Как говорилось ранее, на игры которые не точно выигрышные мы ставим 1 монетку, тогда за 3 проигрыша мы потеряли 3 монетки, 6-3 = 3, тогда мы ставим 3 и выигрываем 6, в сумме имеем 9, то есть, мы ушли в плюс. Теперь рассмотрим ситуацию, когда точно выигрышных игр нет, тогда мы будем ставить всегда 1 монетку. Несложно заметить, что худший случай — ППВППВ.... Тогда перед каждой победой мы проигрываем 2 монетки, 6 — 2 = 4, имея 4 монетки мы ставим одну и выигрываем 2, итого мы имеем опять 6 монеток. В условии сказано, что Саша должен иметь возможность бесконечно не уходить в минус "Другими словами, правда ли, что для любого целого числа n , Саша сможет делать ставки так, чтобы при любых их результатах, не противоречащих описанным выше правилам, в какой-то момент времени у него было хотя бы n монет." В чем я не прав?
About problem E:
Every edge can be included or excluded on any of the k paths. Therefore there are 2^k possible values S[i] can have. Could anyone explain to me, why the set S = {S[1], S[2], ..., S[n]} has at most k different elements?
because when you compress the tree, every node in the tree is either ai or bi (1<=i<=k), so there is at most 2k nodes in the compressed tree
Worst Problemset ever in C it read at least n and in answer the author has considered greater than n
Please do ignore this comment. I think I have figured out why this happens.
Can someone please tell me why my code for B worked after i used
fixed << setprecision(0)
within my code instead of just printing the output like
for(int i=0;i<t;i++){ long long n,m; cin>>n>>m; if(m<=n*2){ cout<<ceil(static_cast<double>(m)/2)<<endl; } else if((m>2*n && m<=4*n-4)){ cout<<ceil(static_cast<double>(m)/2)<<endl; } else if(m==4*n-3){ cout<<(2*n)-1<<endl; } else if(m==4*n-2){ cout<<(2*n)<<endl; } }It failed on testcase 3 which considered the case for a large input like 99999991 399999863 etc...
Sorry if there are any errors in my style of asking for help. This is probably my first comment and I am open to guidance.
For problem $$$E$$$, if $$$paths[i]$$$ is a bit-mask whose $$$j^{th}$$$ bit is set if the $$$i^{th}$$$ edge is within the $$$j^{th}$$$ path, the proof that the number of distinct values in $$$paths$$$ is $$$O(k)$$$ (Please let me know if you notice any incorrect ideas in the proof, or if you want any clarifications):
Claim1: We can can calculate $$$paths$$$ using a recursive DFS. For a node $$$node$$$ whose parent edge is $$$x$$$, given that we calculated $$$paths[y]$$$ for every child edge $$$y$$$ of $$$node$$$, $$$paths[x]=xor\_sum(paths[y]) \oplus xor\_sum(2^z)$$$ (where $$$z$$$ are the indices of paths which have $$$node$$$ as one of its endpoints (if any).
Proof of claim1:
1) Reason for $$$xor\_sum(2^z)$$$: For one of such paths $$$z$$$, if the $$$z^{th}$$$ bit is set in one of $$$paths[y]$$$, this means it is a path that started below $$$node$$$ and ends at $$$node$$$, otherwise, it is a path starting at $$$node$$$ and should move to above $$$node$$$ to reach the other endpoint.
2) For a path with index $$$j$$$, if the $$$j^{th}$$$ bit is set in at least one of $$$paths[y]$$$, we have the following cases:
i) It is set in one of the child edges only, this means it is a path whose one of its endpoints is under $$$node$$$, and the path should move to above $$$node$$$ to reach the other endpoint (or possibly $$$node$$$ itself is the other endpoint as shown in (1)).
ii) It is set in two of the child edges, this means $$$node$$$ is the LCA (Lowest Common Ancestor) of the endpoints of this path.
Based on the previous, a parent edge $$$x$$$ will possibly introduce a new value in $$$paths$$$ only if it has at least $$$2$$$ children edges with non-zero $$$paths$$$ values.
Claim2: The number of such edges $$$x$$$ that will possibly introduce a new value is $$$O(k)$$$.
Proof of claim2:
We can imagine each distinct value in $$$paths$$$ as a connected component. When the $$$j^{th}$$$ bit is set in $$$paths[i]$$$, this set bit could come from any of the $$$j^{th}$$$ path endpoints, so, assume each endpoint introduces a different connected component.
Recalling that $$$y$$$ are the children edges of $$$x$$$, when we xor $$$2$$$ values of $$$paths[y]$$$ as a step towards calculating $$$paths[x]$$$, it is like merging the corresponding $$$2$$$ imaginary connected components. The upper bound of the initial number of connected components is $$$2k$$$ ($$$1$$$ connected component for each path endpoint in isolation). Hence, the upper bound of the merge operations is $$$2k-1$$$, as count of connected components decreases by $$$1$$$ after each merge operation.
I believe the upper bound of non-zero distinct values in $$$paths$$$ is $$$3k-3$$$ (Except for $$$k=1$$$, where we will have 1 non-zero distinct value). An example that demonstrates this upper bound:
For $$$k=5$$$, where the paths are: [20, 13], [21, 11], [19, 9], [17, 7], and [15, 5], we will have $$$12$$$ distinct non-zero values in $$$paths$$$ ($$$3 \cdot 5 - 3$$$), which are (Values of $$$paths$$$ are written in sets for simplicity):
Submission
What does compressed tree mean in E? Any link i can refer to?
ok I found it here.
Do we have to take the worst case scenario every time in C? Like let it be so that we lose consecutively then we get the win. If so, how is 2 3 15 a yes?
How is it no?
I don't understand this test case at all. Please explain it to me is what I'm saying.
Every turn there are two options: you win or you lose. After every win your new value $$$a'$$$ must be greater than $$$a$$$.
Let's make these turns:
1) a $$$15\rightarrow 14$$$ (bet $$$1$$$, first lose)
1) b $$$15 \rightarrow 16$$$ (bet $$$1$$$ but win, $$$16 > 15$$$ so ok)
2) a $$$14 \rightarrow 12$$$ (bet $$$2$$$, second lose)
2) b $$$14 \rightarrow 16$$$ (bet $$$2$$$ but win, $$$16> 15$$$ so ok)
3) a $$$12 \rightarrow 8$$$ (bet $$$4$$$, third lose)
3) b $$$12 \rightarrow 16$$$ (bet $$$4$$$ but win, $$$16 > 15$$$ so ok)
4) Now, if we get to value $$$8$$$ we lose $$$x$$$ in a row, now we bet $$$8$$$ and get value $$$16 > 15$$$
Answer is YES
i get it now. thank you friend.
REGARDING C — (Sasha and the Casino) Can someone please explain how the answer to '2 3 15' is 'YES'? Can you provide me with a combination of bets (Y value and win/loss) that will result in a winning outcome?
$$$[1, 2,4 ,8]$$$ for example
Thanks, man, but I'm still confused. So, out of these four bets, one of them should be a win and three of them are losses. How do you know which one is the winr?
We must choose values so for every possible win we will increase our value $$$a$$$,
Can we use Euler Tour + Greedy for E?
Problem D has a bijection with count of connected induced subgraphs of a tree. I've written about how to prove and construct such a bijection here
deleted
Haha wow...I thought problem B was way harder than any other problem B I've seen. Then again, I have almost zero experience doing these kinds of geometry problems or making observations about them. It was really instructive for me and I thought the solution was very clever. Thanks for this problem.
Can someone prove or disprove this greedy approach for Problem E:
Guessing it should take $$$O(nk)$$$ time for each iteration and we repeat it $$$k$$$ times at worst. Total complexity $$$O(nk^2)$$$ time
Actually we can do it even faster — we may not need to compute the counts from scratch every iteration. Just do it once at the beginning (in $$$O(nk)$$$) and then maintain it dynamically in a map/set like data structure. Thus, overall complexity $$$O(nk\log k)$$$
An update on this. I finally found an example for which the greedy would fail.
Here, the $$$k=6$$$ simple paths would be: $$$(1,2)$$$, $$$(1,3)$$$, $$$(2,4)$$$, $$$(2,5)$$$, $$$(3,4)$$$, $$$(3,5)$$$.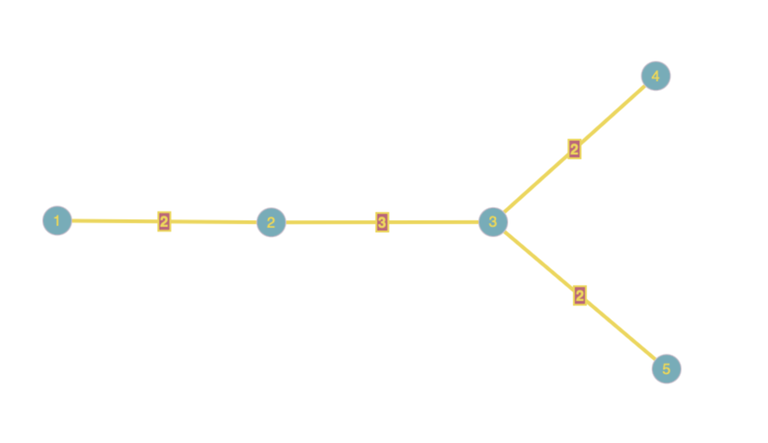 Greedy answer: $$$4$$$
Greedy answer: $$$4$$$
Actual answer: $$$3$$$
We can disprove this approach. Say k = 6. We have three edges in consideration, one covers paths 1 2 3 4, one covers 1 2 5, and the third one covers 3 4 6. Then your algorithm would colour three edges, but we can colour the latter two edges optimally.
In test case: 25 69 231
In the worst case, I would lose 69 times, but on 70th time if I bet 162 (cuz 231 — 69) then i would get 162*25 back, so total money in my pocket would be 3819, which is clearly more than 231, so why is the answer a NO?
I think it's cringe that $$$x \le 100$$$ in C. I don't know how anyone could have allowed the task with 64bit overflow on round.
lele bot we are
может кто нибудь подробнее пояснить формулу из разбора F "А это известная задача и таких вариантов $$$\binom{R - L + len}{len}$$$"?
.
Why in problem C, Test case 3 3 6 is a NO? Let's say I lose 3 times first, each time I bet 1 coin and lose, then I am left with 3 coins. Now I bet all 3 coins and get 3*3=9 coins back, which is more than initial coins. Someone please explain!
please note that casino can choose to win or not at any time, so at the third time you bet 1 coin, casino will choose to lose, and you'll end up with 6 coins, which is same as the number of coins you started with.
At the end of each turn, player has to bet enough such that he ends up with at least 1 more than his initial. This is because he does not know if he will win or lose.
Based on the above mentioned, the most conservative betting strategy is to bet 1,1,2. But this means that he does not have enough at the end.
If the sequence is Lose, Lose, Win, player will end with 8 which is more than 6.
If the sequence is Lose, Lose, Lose, player will end with 2. But he can bet 2 afterwards knowing he will definitely win and end with 6 (2+Y(K-1))
Player has to assume the worse and bet 2 on the third move. But this means he will end up with the same he started off with, thus a NO.
Is problem c inspired from here ?