Given an array of size n.You need to select those two different indices such that quirk between them is maximum.Quirk Q(i,j)= 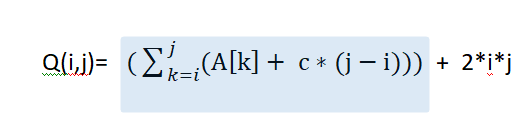
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 151 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/21/2024 14:50:19 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Auto comment: topic has been updated by ram396 (previous revision, new revision, compare).
Can elements of A be negative?
No
Well if elements aren't negative then j should always be equal to n. And i you can traverse in linear time to find the maximum.
Edit: only if c is +ve, otherwise j can be other things.
If $$$A[i]$$$ or $$$c$$$ is allowed to be negative:
Note that:
We define the following functions:
For each $$$j$$$, you need to find $$$i$$$ such that $$$F(j) + M(i)j + C(i)$$$ is maximized. You can use convex hull trick to do so in $$$O(N \lg N)$$$ time.
That is a wonderful new thing which probably won't be useful for me to learn at this stage, but can you take a quick look at the latest question I asked in my blogs here? I think this problem can be solved using what you call a "convex hull trick" ? Am I right?. In brief I want the maximum of $$$a_1(K - i) - b_1, a_2(K - i) - b_2, \ldots, a_n(K - i) - b_n$$$ after each time I change i from 0 to K — 1.
can u provide the code?