Тема данного поста — не нова, но, наверняка, кому-нибудь пригодится:) Начнём с примера задачи, в которой используется дерево отрезков.
Имеется массив из n (n≤10^5) целых чисел, нужно находить сумму на отрезке от l до r (0≤l,r≤n-1) и изменять значение i-го
(0≤i≤n-1) элемента. Количество запросов m (m≤10^5).
Очевидно, что наивное решение работает за O(n*m), а дерево отрезков дает возможность решать данную задачу с асимптотикой O(m*log2n).
Существует множество разных видов деревьев отрезков. В данной статье дерево отрезков – структура данных, которая по имеющейся последовательности из n чисел умеет выполнять быстро (за логарифмическое время) 2 вида запросов:
1) Изменить значение i-го элемента
2) Вычислить значение некоторой фиксированной ассоциативной функции на отрезке от l до r.
Что же собой представляет дерево отрезков(ДО)? ДО – бинарное дерево (обычно, для удобства дополняют до полного нулевыми элементами), в котором листьями являются элементы исходного массива, а в каждой вершине записано значение функции f от двух сыновей. То есть в листах записано значение функции на отрезке длинной 1, в родителе записано значение функции на отрезке длинны 2, в родителе которого – 4… таким образом, в каждой вершине записано значение функции на некотором отрезке, что и послужило поводом для такого названия.

Для нашего примера задачи функция f – сумма, тогда ДО для четырех элементов будет выглядеть следующим образом:
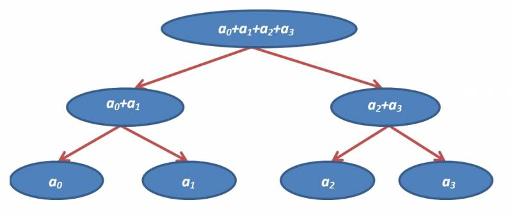
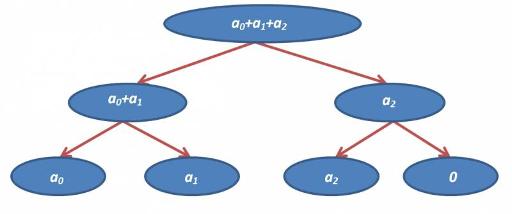
Если же у нас количество элементов (n) не является степенью двойки, то мы дополним их нулями. (В общем случае, когда мы работает с типом данных Т и функцией f, то ноль — такое значение, что для любого x из T верно f(x,ноль)=x.) Например, ДО сумм для 3 элементов будет выглядеть так:
Как же хранить ДО? Существует 2 способа:
• структуры на указателях;
• линейный массив.
На сколько мне известно, первый способ используют только для персистентных ДО. Мы же пока разбираем самую обычную и простую модификацию ДО, поэтому воспользуемся вторым способом. Создадим линейный массив a из 2*nMax элементов, где nMax – наименьшая степень двойки, которая не превосходит n. В первом элементе (a[1]) будем хранить корень дерева, а для каждой вершины i её сыновья хранятся в ячейках с номерами 2*i (левый сын), 2*i+1 (правый сын). Почему для хранения достаточно 2*nMax элементов? Мы имеем nMax листов, у них nMax/2 родителей, у них nMax/4 … и 1 корень, очевидно, что эта сумма (1+2+4+…+ nMax/4+ nMax/2+ nMax) равняется 2*nMax-1.
На рисунке проставим возле каждой вершины ее индекс в массиве:
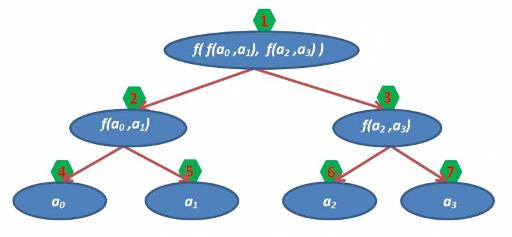
А в массив дерево будет уложено следующим образом:

Теперь определим, какие операции мы хотим выполнять с нашим ДО:
1) построить ДО;
2) узнать значение i-го элемента;
3) изменить значение i-го элемента;
4) найти значение функции на отрезке от l до r.
Разберем по очереди все операции.
1 Построить дерево отрезков.
Пусть у нас есть массив b из n элементов. Для начала нам нужно найти nMax (наименьшая степень двойки, которая не превосходит n). Это можно реализовать как через формулу:
nMax = (1 << (int)(log2(1.0*(n-1)) + 1);
так и простеньким циклом:
nMax= 1;
while (nMax<n) nMax<<= 1;
Далее нужно заполнить массив a нулями (соответствующего типа) и заполнить листы ДО значениями из массива b (мы помним, что в ДО индексы листьев от nMax до 2*nMax-1):
for (int i=0; i<n; i++)
a[nMax+i]= b[i];
На данный момент имеем:
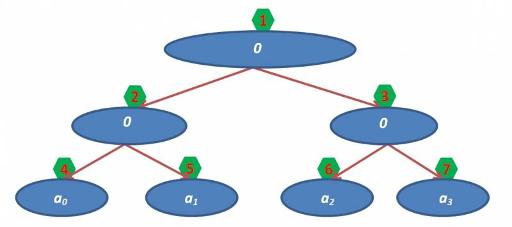
Теперь осталось только заполнить значения во всех родителях. Это можно сделать за один линейный проход (помним, что у i-ой вершины сыновья с индексами 2*i и 2*i+1, а в вершине мы храним значение функции от двух сыновей):
for (int i=nMax-1; i>0; i--)
a[i]= f(a[2*i],a[2*i+1]);
Таким образом мы построили ДО с асимптотикой O(nMax) = O(n).
2 Узнать значение i-го элемента.
Как уже писалось ранее у нашего ДО листья имеют индексы от nMax до 2*nMax-1, поэтому значение i-го элемента элемента находиться в ячейке с индексом nMax+i: return a[nMax+i] Очевидно, что данный запрос выполняется за константу.
3 Изменить значение i-го элемента.
Если мы изменим значение в листе дерева, то все значения на пути к корню от данного листа перестанут соответствовать действительности, поэтому их нужно пересчитать, в остальных же останутся корректные значения. Как известно, глубина полного бинарного дерева из m вершин равна log2m, поэтому мы должны выполнить данную операцию за логарифмическое время. Например, изменим a2 на a2 I :
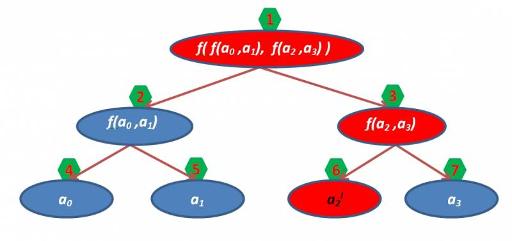
Красным цветом выделены вершины, в которых нужно изменить значения.
Что бы «обновить» ДО нам нужно записать в лист новое значение, а затем подняться до корня, каждый раз пересчитывая значение функции в вершине. Изменить значение в листе очень просто (вспомним, что индексы листьев от nMax до 2*nMax-1). Значение i-го листа имеет индекс nMax+i :
a[nMax+i]= newValue;
Теперь осталось подняться до корня, это можно сделать с помощью цикла:
while (i>1)
{
i/= 2;
a[i]= f(a[2*i],a[2*i+1]);
}
4 Найти значение функции на отрезке от l до r.
Наконец-то, мы добрались до самого интересного запроса. Стоит отметить, что частный случай, когда l=r разобран в пункте 2 и выполняется за константу, в общем же случае асимптотика логарифмическая.
Введем определения.
Фундаментальный отрезок – такой отрезок, для которого существует вершина в дереве, хранящая значение функции на данном отрезке.
Уровень. Уровень корня – 1, а для каждого сына уровень на единицу больше, чем у родителя.
Для того, что бы вычислить значение функции на отрезке, нам необходимо разбить его на МИНИМАЛЬНОЕ количество фундаментальных отрезков. Что бы найти значение для любой вершины (кроме листа), нам нужно знать значения для сыновей. Мы будем спускаться по ДО. Изначально встаем в корень. Пусть мы находимся в какой-то вершине. Рассмотрим 3 возможных случая: отрезок [l..r] совпадает с отрезком, соответствующим текущей вершине, отрезок [l..r] полностью принадлежит одному из сыновей, отрезок принадлежит обоим сыновьям. В первом случае просто возвращаем посчитанное значение из ДО, во-втором – спускаемся в данного сына, в-третьем же случае разобьем данный отрезок на два: [l..правый конец левого сына] и [левый конец правого сына..r]. Рекурсивно вычислим значения для каждого из них.
Рассмотрим на примере. Пусть у нас есть ДО для 8 элементов, запишем, какой отрезок соответствует каждой вершине:
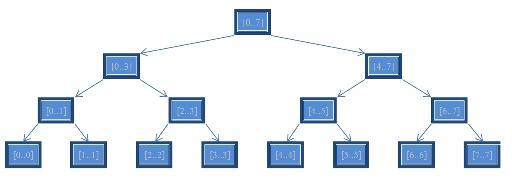
А теперь посмотрим, как будет выполняться запрос для отрезка [1..5].
Сначала встаем в корень — наш отрезок принадлежит обоим сыновьям. Значит, нам нужно разбить его на 2 отрезка: [1..3] и [4..5]. Для каждого из них рекурсивно вычислить значение. Далее отрезок [1..3] опять принадлежит 2 сыновьям, разбиваем его на 2 отрезка: [1..1] и [2..3]. Отрезок [1..1] принадлежит только правому сыну, спускаемся в него и видим, что отрезок [1..1] – фундаментальный. Берем для него значение из вершины, и поднимаемся до 2 уровня (вершина [0..3]). Для левого сына мы уже рекурсивно посчитали, теперь посчитаем для правого: спускаемся в него. Отрезок [2..3] – фундаментальный, берем значение из вершины. Возвращаемся в [0..3] и уже можем вычислить значение для отрезка [1..3], так как значение функции уже вычислили для обеих его частей. Возвращаемся в корень и спускаемся в правого сына [4..7], наш подотрезок ([4..5]) принадлежит только одному левому сыну, спускаемся в него. Вершине соответствует отрезок [4..5], следовательно, он — фундаментальный, берем из вершины значение. Возвращаемся в корень и вычисляем ответ.

Почему этот запрос выполниться за логарифмическое время? Как известно, глубина (количество уровней) дерева из n вершин равняется log2n, кроме того, утверждается, что на каждом уровне мы посетим не более 4 вершин, таким образом, мы посетим O (log2n) вершин. Рассмотрим код. Для вычисления значения на отрезке нам понадобится вызвать рекурсивную функцию от 5 аргументов, для удобства напишем функцию, которая по 2 аргументам (границы отрезка для запроса) вызывает функцию 5-и аргументов и возвращает значение:
T query(int l, int r)
{// return value function f on the segment [l;r]
return query(l,r,0,nMax-1,1);
}
Теперь наша рекурсивная функция:
T query(int l, int r, int leftPosition, int rightPosition, int v)
{// return value function f on the intersection segments [l;r] and [leftPosition;rightPosition]
// l – левая граница запроса
// r – правая граница запроса
// v – текущая вершина дерева отрезков
// [leftPosition; rightPosition] – отрезок соответствующий v
if (r<l) return zero;
//если отрезок не существует, то возвращаем ноль.
if (l==leftPosition && r==rightPosition) return a[v];
// если отрезок фундаментальный,то возвращаем значение из вершины
// раз мы дошли сюда, то отрезок принадлежит сыновьям
int middle= (leftPosition+rightPosition)/2;
// вычисляем правую границу левого сына
return f(query(l,min(middle,r),leftPosition,middle,v*2),
query(max(l,middle+1),r,middle+1,rightPosition,v*2+1));
// рекурсивно вычисляем запросы для сыновей
}
Мой код класса дерево отрезков единичная модификация.
Скоро выложу несколько примеров задач с решениями с использованием опубликованного класса.
P.S. Буду рад конструктивным замечаниям/предложениям по написанию статьи/кода
UPD: вот примеры










