pedromnasc's blog

Live Archive 6669 — Hidden Tree
By pedromnasc, 10 years ago, In English

How can i solve this problem: https://icpcarchive.ecs.baylor.edu/index.php?option=onlinejudge&page=show_problem&problem=4681 ? I only think on slow DP solution.

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 2   Vote: I like it +2 Vote: I do not like it

EDIT: Xellos has pointed out my mistake. sorry for the comment. :)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    It doesn't, because (2,1) don't form a balanced subtree.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      thanks, edited.
      also, ur comment gave me an idea about the solution. thanks for that too. :D

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Pro tip: there is no need to "erase" your comment just because it's wrong :) The edit function should only be used to fix grammar or to add info.

        → Reply
»
10 years ago, # |
  Vote: I like it +6 Vote: I do not like it

for every BBT, there's a unique odd number a such that all leaves have weights a2k. Therefore, we can split our sequence into multiple disjoint sequences of elements that give the same odd number after we keep dividing them by 2 as long as possible. The sum of these sequences' lengths is N, so we just need to be able to find the largest hidden BBT in each of them, probably in O(N2) or so time.

Or not. I got AC with optimized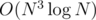 , in 9.4 seconds :D

The basics is just a simple bruteforce: consider all A[i] just powers of 2 (the situation for a sequence with common a, after dividing by it and just taking the 2k part). Now, consider V[k][i][j]: the maximum number of vertices in a tree hidden in A[i..(j - 1)] with sum 2k. It's clear that if A[i] = 2k, then V[k][i][i + 1] is at least k; for trees with at least 1 vertex, we can split them into a subtree in A[i..(l - 1)] and a subtree in A[m..(j - 1)], with l ≤ m and equal sum in both, or equivalently make a new array ; then, we get for the maximum tree hidden in A[i..(j - 1)] with k + 1 vertices

This is obviously slow, but there are several good points about it:

  • $V[][i][j]$ only marks trees that include elements A[i] and A[j - 1], so there'll be less situations where it's non-zero, in non-border cases (like "1000x 1")

  • M[k][l][j] is non-increasing for increasing l, so if V[k][i][l2] < V[k][i][l1] and l2 > l1, we know that l = l2 doesn't give solutions better than l1 and we can just ignore it; this is useful in my implementation, which tries first pairs (i, l) and only if there's been no larger tree for the same i and smaller l (that also includes "empty trees") does it try all j

  • time limit: 10 s; most likely, many of the 50 mentioned cases would only produce several smaller sequences with identical a, and it helps the complexity greatly

  • the actual number of increasing triples (i, l, j) is about 1.5·108 for N = 1000

All of this together helps my solution pass (even though it could still be optimized, for example by fast maximum function and checks that'd help avoid computing maximums when it's not necessary).

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    I thought in the recurrence relation with the same complexity, but i didn't realize all these optimizations! Also i didn't believe it could pass even optimizing. Thanks!

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      I'd like to know the original solution's complexity. I didn't find any analysis on the net, but since it's from a rather recent regional, maybe there could be someone here who encountered it...

      → Reply