Я временно перестал участвовать в соревнованиях по "личным обстоятельствам", но продолжаю урывками прорешивать задачки на разных сайтах. Напоролся на задачку (точнее мой генератор случайных чисел напоролся на задачку) 8843 Complete the Set.
Честно говоря ничего в голову не приходит — судя по параметрам задачи — 1100 случаев в одном тесте, 65536 чисел в одном сете — полный перебор вряд ли пройдёт, я имею в виду каждое число с каждым пробовать по OR и AND пока не перестанут появляться новые числа. (хотя бы понятно, что в такой ситуации не надо пробовать что-то большее, чем пары чисел — уже прогресс от "absolute brute force").
Но в голове вертится одна из недавних задачек с Topcoder, где нужно было смешивать краски с помощью XOR и решалась она элегантно гауссовой элиминацией — может быть и здесь какая-нибудь хитрость?
Задачка не очень порешенная, "запылившаяся", решило её меньше 50 человек и разборов в интернете я не нашёл. Если знаете как решать, подскажите только идею — в какую сторону копать.
Большое спасибо!
Это очень медленное решение, но оно получило AC (за 1.01 секунды).
Пусть побитовый XOR это
, OR — 
, AND — 
.
Пусть n — количество чисел в тесте, k — разрядность (в условии k = 16)
Сперва заметим, что добавление к нашему множеству 0 не меняет свойства из условия. Поэтому можно удалить из множества 0, а потом (в зависимости от того, равен ли побитовый AND всех остальных чисел 0 (то есть можно ли получить 0 из остальных чисел)) либо оставить ответ как есть, либо уменьшить его на один (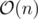
).
Пусть у нас есть несколько ненулевых чисел a1, a2, ..., an. Пусть
Пусть 
. Тогда ответ для a1, ..., an, очевидно, равен ответу для b1, ..., bn. Перейдём к задаче для b1, ..., bn (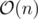
)
Сгенерируем (например, за
, возможно, можно и быстрее) следующие маски mask1, ..., maskk: в maski j - тый бит равен 1, если при всех k от 1 до n в числах bk либо установлен j-тый бит, либо не установлен i-тый; иначе этот бит равен 0.
Фактически мы сделали следующее. Пусть Si — множество чисел q от 1 до n, что в bq i-бит равен 1. Тогда для каждого i мы выделили те j, что
.
Теперь пусть
. Будем проверять то, лежит ли число v в нашем множестве так:
1)
(
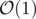), то есть v — подмаска M.
2) Пусть С —
всех maski для таких i, что i-тый бит v равен 1. Тогда надо, чтобы 
, то есть С подмаска v. (
).
Теперь просто проверим все числа за
. Итоговая асимптотика равна 
на тест.
Я хотел бы ещё написать, почему это работает, но этот комментарий уже слишком длинный (а объяснение ещё раза в два длиннее). Поэтому это я сделаю в следующем комментарии.
UPD. Перебор в конце можно делать рекурсивно, немного улучшив асимптотику и время работы.
UPD 2. maski есть просто AND всех чисел b, у которых i-тый бит равен 1, то есть маски можно посчитать за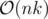
. Итого (в совокупности с UPD 1) можно добиться асимптотики 
на тест.
Спасибо большое — в следующий свободный час буду разбираться. В том числе, почему работает. Борьба с задачей впечатляет (смотрю по submissions участника по имени Владислав, видимо вы). Финальное время, насколько вижу, 0.69, и оно на уровне лучших решений. Так что, видимо, так оно и должно решаться.
Потом они ещё это дело гоняют на Pentium III cluster, так что на Codeforces или любом другом сайте оно бы работало быстрее.