Здраствуйте. Во время написания игры столкнулся с задачей, которую не могу решить. В игре у вас есть меч и им надо отбивать пули. На каждой итерации меч (для начала, я хотел бы решить, упростив его модель до отрезка) подвергается двум геометрическим преобразованиям:

1)Точка, относительно которой он вращается совершает перемещение на вектор v из позиции (x0;y0)

2)Все остальные точки меча вращаются относительно нее на угол omega.

На каждой итерации пуля перемещается на вектор z. Изначально она находится в точке (m;n)

Меч должен отбивать пули, с которыми столкнулся. Разработка ведется в Unity3D, с физическим движком PhysX. Как оказалось, его стандартной точности не хватает для расчета этих преобразований и пули застревают в мече.

Использование различных скриптов, разработанных сообществом Unity для решения этой проблемы мне не помогло. Увеличение количества итераций физического движка в секунду исправляет ошибки при столкновении, но убивает производительность. Подробнее я писал в answers.unity3d.com, но получил только решения для случая, когда движется либо меч, либо пуля, но не то и другое сразу. (http://answers.unity3d.com/questions/749102/collision-of-fast-objects-does-not-work-yes-i-goog.html)

Поэтому, я решил написать обработку этого вида столкновений с нуля.

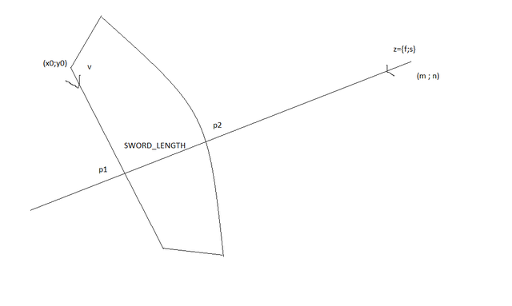
(Длина меча постоянна, просто картинка не совсем точна).

Vector2 — класс двухмерного вектора. magnitude() возвращает его длину, normalized() возвращает коллинеарный ему вектор длины 1.

p1 и p2 — точки пересечения траектории пули и траекторий неподвижной точки меча и точки меча, наиболее удаленной от неподвжной соответственно

Определим функции

Line line_from_vector_and_point(Vector2 vec, Vector2 p)

Vector2 lines_intersection(Line l1, Line l2)

float points_distance(Vector2 p1, Vector2 p2)

смысл которых соответствует названию.

Далее, можно найти Vector2 p1=lines_intersection(line_from_vector_and_point(v,new Vector2(x0,y0)),line_from_vector_and_point(z,new Vector2(m,n)));

Vector2 p2=p1-z.normalized()*SWORD_LENGTH;

Пусть tb(r) — функция, которая по расстоянию r точки отрезка p1;p2 от p1 возвращает время, за которое пуля достигнет этой точки.

Пусть ts(r) — функция, которая по расстоянию r некоторой точки отрезка меча от оси вращения этого меча возвращает время, за которое данная точка окажется на отрезке p1;p2

Я предположил, что f(r)=ts(r)-tb(r) — унимодальная функция, при условии, что omega всегда менее 180 градусов и попытался это доказать. Если это верно, то точку столкновения можно определить троичным поиском.

tb(r)=(points_distance(new Vector2(m,n),p1)-r)/z.magnitude()

К сожалению, выразить ts(r) я не смог.

Координаты точки меча от радиуса и времени выражаются как

(x0+v.x*t+r*cos(omega*t);y0+v.y*t+r*sin(omega*t))

ts(0) легко найти как points_distance(new Vector2(x0,y0),p1)/v.magnitude(), т.к. речь идет о точке меча, движущейся по прямой, но остальные перемещатся по кривым, длину участка и скорость прохождения которых у меня не получается определить.

Есть ли способы найти ts(r), или упростить модель столкновения?

Заранее благодарен.