Rubanenko's blog

TopCoder SRM 628
By Rubanenko, 10 years ago, In English

It seems corresponding thread was not created by anybody else...

How to solve 1000?

  • Vote: I like it
  • +14
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 4   Vote: I like it +24 Vote: I do not like it

Well, my idea was the following: What should we do? Try each round for at least 1 star (each one independent), then some easiest (by Y) of rest rounds to 2 stars (each one independent again)

Note, that if some hard(by Y) rounds are with 1 star and we need more 2stars it doesn't make sense to have 1 on easy round. So the solution:

Sort by Y, then have a dynamic programming dp(A rounds left,B 2stars needed). If A=B then you need get 2stars on current, else it's not important and you will get 2stars with probability x/(x+y).

And you need fact that if probability of smth is p, then it'll take 1/p turns to first success, but it was even mentioned in sample description.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

500?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Note, that the result is sum of some elements of an array. Suppose we are allowed for B choose any of the branches(it doesn't change anything because max is not less then any).

    Suppose we fixed branch for each B, and there's t 'X'es here, then the best result is the sum of t max elements of given array.

    So we need just maximize the number of X'es, so we need choose max of Xes in each B. All you need now is to parse input

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    First notice that eventual answer is a sum of some conductors. To make a maximum of a sum where one can choose summands from a predefined set, we should obviously pick the biggest summands. So the only thing that matters is the number of summands. How do we find the maximum number of summands? Treat each X as 1 and run a simulation.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    This expression forms a rooted binary tree, with three types of nodes: A-node, B-node and X-node. Let's count how many values can be lifted from the leaves to every vertex v(let's call it f(v)). Note, that every X-node is a leaf, and naturally f(v) = 1. If v is a A-node, then f(v) equals to f(u1) + f(u2) where u1 and u2 are children of v. As you have already guessed, f(v) for B-node equals to max(f(u1), f(u2)). Now we can see that the answer will be no more than sum of f(root) values. One can always place elements of a given array in such a way to get maximal f(root) elements in the result. So the solution is counting f(root) and summing up f(root) biggest elements in the array.

    → Reply
»
10 years ago, # |
  Vote: I like it -25 Vote: I do not like it

You must train and quickly solve all first problem before foward 1000 problem!

→ Reply
»
10 years ago, # |
  Vote: I like it +21 Vote: I do not like it

Even though quite late, I'll explain my approach:

First, if the probability of successfully solving a level is p, then the expected time of solving it is 1 with probability p or E + 1 (starting from the same situation) with probability 1 - p, so

Sort the levels by increasing $y$ and try solving them in that order. For solving level i, we take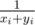 expected time and get 0 or 1 additional stars (subtract N from m). There's a critical point where, after solving i levels, out of which we only got 0 additional stars for the i-th, we realize that OSHIT, we need N - i more stars, but only have N - i levels left. The optimal strategy, due to sorting (our chances are the best with these N - i levels), is solving these N - i remaining levels each for 1 additional star. Since we can treat it as winning with probability only yi, the expected time for it is .

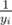What now? Suppose we knew probabilities Pi, j that after solving i levels, we get j additional stars. Then, the probability of the OSHIT moment after solving i levels is : we must've gained exactly m - (N - i) additional stars in levels 1..i - 1 and 0 in level i (which gives the term 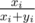). Also, in this situation, total expected time is .

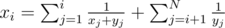There are 2 special cases here:

  • m = 2N originally: the OSHIT moment happens at the beginning of the game (so for i = 0), with probability p0 = 1; we need time
  • we can win the game even without such situations, if we get strictly more than m additional stars just by playing to complete all levels; that gives time with probability

Any win must fall into exactly one of these situations, so the total expected time is

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Your derivation of formula for E lacks proving that this is finite :D.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Good thing it isn't a math competition... speaking of which, IMO did have a problem with optimization scoring this year

      → Reply
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Anybody knows when will be next srm?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You will know, when they will send you an e-mail. Oh, sorry, they don't send e-mails or send them 2h before SRM ; d.

    → Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

To find root of number or to say that it doesn't exist I usually write like that:

(1 <= n and n <= 10 ^ 18)
int get(ll n) { 
  ll x = (ll)sqrt(x + .0);
  if (x * x == n) return x;
  return -1;
}

But after this SRM(div1 250) I noticed that more experienced coders more careful; For example: Mimino used binary search to find SQRT of N, also sdya's code differs from mine.

bool getRoot(long long n) {
  long long m = (long long)(sqrt((double)(n)));
  for (long long i = m - 2; i <= m + 2; ++i) {
    if (i >= 1 && i * i == n) {
      return true;
    }
  }
  return false;
}

Is there some testcases where my code doesn't work?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    For me it sounds like some joke) Few years ago I heard from one guy who participated in ACM ICPC WF something like no, never simply take sqrt(), you should check in range at least +-5 from sqrt(n), because of precision problems; and he was absolutely serious:). At that moment I even thought "ok, well, thanks for great advice!", but now it just sounds funny for me. Just can't understand why lot of guys are doing it this way. For me it is just like doing integer binary search with while (l+10<r) and then checking all remaining numbers in range l..r.

    Of course, you are free to do whatever you want, but there is no need in such complicated stuff)

    Talking about precision problems, i'll just write sqrt(x + .5); instead of sqrt(x + .0);

    I guess i used this code few hundred times during past few years, and never had any problems with it. In case I am wrong and it is actually bad idea to search square root in this way — i'll be glad to read some detailed explanation:)

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You know that double do not store integer numbers up to 1e18 precisely, right?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sure. It gives ~15 digits, right?

        But can you provide some testcase to fail this straightforward approach?

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it -8 Vote: I do not like it

          You asked why people do it

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Ok, thanks) Now i'll even try some bruteforce to crack this solution) For me it was obvious that if it is possible — almost every author will add such testcase, but so far i never seen it. And I thought that it implies quality of such approach)

            → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Firstly, if x has more than 15 digits, then x + 0.5 = x in doubles is possible, in which case, there's no point in relying on it at all.

          Depends on what you want to do. If you just want to check if an integer is a square or find its square root, then yes, you shouldn't need checking any range, just rounding and checking if the first guess from sqrt- works.

          Consider just a little bit more complex task: find the closest square root to a given number. whoops, just a little bit off... (it's for square root of 1018 - 1, in case you don't want to count 9s) Nope, that's not the right answer...

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it -8 Vote: I do not like it

            My compiler shows 1000000000 and 1. I have no idea why. Where I can find good compiler? (C++)

            → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            And why that code should provide right answer? It don't have to — even with precise calculations. Theoretically it should give rounded down sqrt(x), not closest root. Actually it does not (check this), but that is not the point:)

            BTW, just finished checking of all numbers x*x+t for x<=1e9, abs(t)<=20, naive algorithm passed. It often gives wrong value of floor(sqrt(x)), but works well if we just need to find root or say that it does not exist. BackendDeveloper, thanks for interesting question)

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              10 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              This really is bait, huh? I'll chomp on it anyway... sigh

              This is still an incredibly simple example, but you already get weird results — it gives a different result for BackendDeveloper, "theoretically" fails... now imagine getting numbers that you can't store in a long long, larger roots, whatever there could be — you never know where you'd need some kind of precaution.

              And think which is better: make your code a few lines longer, wasting a minute on each problem with such stuff (when you have it all trained well), or occasionally fail something? There's such a thing as "good practice", you know?

              UPD: I failed a lot with straightforward pow() on this problem

              → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        One can use long double instead of double (in C++, of course). Also it's sufficient to store the first 9-10 digits to obtain sqrt(N) accurate up to 1. The last thing is that sqrt(N) will not be greater than the actual value of square root of N, so it's enough to check only floor(sqrt(N) + eps) as a candidate for square root of N.

        → Reply