Hello, I'm currently learning how to use matrix exponentiation to solve linear recurrence relations, and I'm in doubt on how to build transformation matrices, for example.
Let f(n) = 2 * f(n - 1) + 2 * (f - 2) + 2 * f(n - 3) + f(n - 4)
With f(1) = a, f(2) = b, f(3) = c, f(4) = d
The vector v with the initial values should be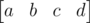 
How to build it's transformation matrix ?
You are looking for a matrix A such that if you take the vector ( f(n-4), f(n-3), f(n-2), f(n-1) ) and multiply it by A you will get the vector ( f(n-3), f(n-2), f(n-1), f(n) ) for any n. Knowing this property, can you see how A must look like?
Hello, it's an honor to be answered by misof.
I've got an matrix with an alike property, but it only works for f(5). For a initial matrix of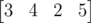
. f(6) = 46. But this current matrix gives me 68.
Could you point what is wrong in this transformation matrix ?
68 is correct. With [3, 4, 2, 5] f(5) will be 25. Now we have [4, 2, 5, 25], f(6) = 25 * 2 + 5 * 2 + 2 * 2 + 4 = 68.
Thank you, actually, it's right, I had an mistake in my recurrence relation, thanks.
Let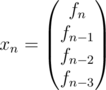
and 
. 
.
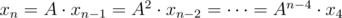now u can see that
just handle cases when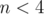
separately, otherwise find 
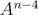(can be done in 
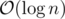) and multiply it with 
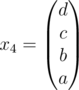to get 
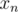(whose first element will be 
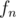, which is exactly what u want).