Hello
I am trying to solve this problem from hackerrank.
In short, there is a tournament graph, which is directed complete graph, i.e for every (u, v), where u < v there is an edge either from u to v, or from v to u.
We know scores of each player (i.e out degrees of each vertex), but some scores might be erased. Instead of erased scores we can put any scores, so that for these scores should exist a tournament graph. How many possible variants exists?
My thoughts (which can help to solve this problem):
To check (s[1], s[2], .., s[n]) sequence is out degrees of tournament graph, must hold:
if we sort sequence, so that s[1] <= s[2] <= .. <= s[n]
1.
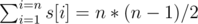
2.
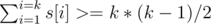, for every k = 1 .. n-1
I though to solve this problem using dynamic problem and these properties, but it was wrong.
So How to solve this problem?
I did it, Accepted.
Observations:
Two conditions in another word:
First of all we need to check not erased scores, just using 1 condition. Then put erased scores using dynamic programming.
Let's denote erased scores b[i], not erased scores a[i];
So we can pre calculate for every k, minimal value of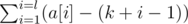
, let's denote it exceed[k].
Dynamic programming:
states:
dp[k][score][sum]: we know first k minimum erased scores, and their values not exceeds score, and sum is their sum.
transitions:
Skip score, dp[k][score][sum] += dp[k][score + 1][sum];
Put i scores of value score dp[k][score][sum] += C[m — k][i] * dp[k + i][score + 1][sum + i*score], where m number of erased scores, C[n][k] = combination.
my code