How many operations will have $$$x = 0$$$.

Try $$$k = 2$$$.

If $$$k$$$ is 1, we can only subtract 1 in each operation, and our answer will be $$$n$$$.

Now, first, it can be seen that we have to apply at least $$$n$$$ mod $$$k$$$ operations of subtracting $$$k^0$$$ (as all the other operations will not change the value of $$$n$$$ mod $$$k$$$). Now, once $$$n$$$ is divisible by $$$k$$$, solving the problem for $$$n$$$ is equivalent to solving the problem for $$$\frac{n}{k}$$$ as subtracting $$$k^0$$$ will be useless because if we apply the $$$k^0$$$ subtraction operation, then $$$n$$$ mod $$$k$$$ becomes $$$k-1$$$, and we have to apply $$$k-1$$$ more operations to make $$$n$$$ divisible by $$$k$$$ (as the final result, i.e., 0 is divisible by $$$k$$$). Instead of doing these $$$k$$$ operations of subtracting $$$k^0$$$, a single operation subtracting $$$k^1$$$ will do the job.

So, our final answer becomes the sum of the digits of $$$n$$$ in base $$$k$$$.

The complexity of the solution is $$$O(\log_{k}{n})$$$ per testcase.

#include <bits/stdc++.h>
using namespace std;
 
int find_min_oper(int n, int k){
	if(k == 1) return n;
	int ans = 0;
	while(n){
		ans += n%k;
		n /= k;
	}
	return ans;
}
 
int main()
{
	int t;
	cin >> t;
	while(t--){
		int n,k;
		cin >> n >> k;
		cout << find_min_oper(n,k) << "\n";
	}
    return 0;
}

The final state of $$$i$$$th bulb (on or off) is independent of $$$n$$$.

The final state of the $$$i$$$th bulb tells us about the parity of number of divisors of $$$i$$$.

For any bulb $$$i$$$, its final state depends on the parity of the number of divisors of $$$i$$$. If $$$i$$$ has an even number of divisors, then bulb $$$i$$$ will be on; else it will be off. This translates to, if $$$i$$$ is not a perfect square, bulb $$$i$$$ will be on; else it will be off. So now the problem is to find the $$$k$$$th number which is not a perfect square. This can be done by binary searching the value of $$$n$$$ such that $$$n- \lfloor \sqrt{n} \rfloor = k$$$ or the direct formula $$$n$$$ = $$$\lfloor k + \sqrt{k} + 0.5 \rfloor$$$.

For the proof of the second formula you can refer this book page 141 E18

#include <bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin >> t;
    while(t--){
        long long k, l = 1, r = 2e18;
        cin >> k;
        while(r-l > 1){
            long long mid = (l+r)>>1;
            long long n = mid - int(sqrtl(mid));
            if(n >= k) r = mid;
            else l = mid;
        }
        cout << r << "\n";
    }
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin >> t;
    while(t--){
        long long k;
        cin >> k;
        cout << k + int(sqrtl(k) + 0.5) << "\n";
    }
    return 0;
}

Try to find some independent operations/combinations.

The expression is independent for each digit in binary representation

The first observation is that the expression $$$a$$$|$$$b$$$ - $$$a$$$&$$$c = d$$$ is bitwise independent. That is, the combination of a tuple of bits of $$$a, b, and\ c$$$ corresponding to the same power of 2 will only affect the bit value of $$$d$$$ at that power of 2 only.

This is because:

1. We are performing subtraction, so extra carry won't be generated to the next power of 2.

2. Any tuple of bits of $$$a$$$, $$$b$$$, and $$$c$$$ corresponding to the same power of 2 won't result in -1 for that power of 2. As that would require $$$a|b$$$ to be zero and $$$a$$$&$$$c$$$ to be one. The former condition requires the bit of $$$a$$$ to be zero, while the latter requires it to be one, which is contradicting.

Now, let us consider all 8 cases of bits of a, b, c and the corresponding bit value of d in the following table:

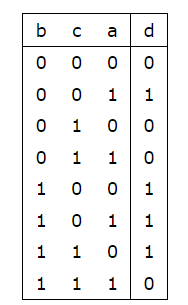
So, clearly, for different bits of $$$b, c,$$$ and $$$d$$$, we can find the value of the corresponding bit in $$$a$$$, provided it is not the case when bit values of $$$b, c,$$$ and $$$d$$$ are 1,0,0 or 0,1,1, which are not possible; so, in that case, the answer is -1.

#include <bits/stdc++.h>
#define ll long long
using namespace std;
 
void solve() {
    ll a = 0, b, c, d, pos = 1, bit_b, bit_c, bit_d, mask = 1;
    cin >> b >> c >> d;
    for (ll i = 0; i < 62; i++) {
        if (b&mask) bit_b = 1;
        else bit_b = 0;
        if (c&mask) bit_c = 1;
        else bit_c = 0;
        if (d&mask) bit_d = 1;
        else bit_d = 0;
        if ((bit_b && (!bit_c) && (!bit_d)) || ((!bit_b) && bit_c && bit_d)) {
            pos = 0;
            break;
        }
        if (bit_b && bit_c) {
            a += (1ll-bit_d)*mask;
        } else {
            a += bit_d*mask;
        }
        mask<<=1;
    }
    if (pos) {
        cout << a << "\n";
    } else {
        cout << -1 << "\n";
    }
}
 
int main() {
    ll t;
    cin >> t;
    while (t--) {
        solve();
    }
}

The value of $$$d$$$ is very small.

Try using Disjoint Set Union (DSU).

The main idea is to take advantage of the low upper bound of $$$d_i$$$ and apply the Disjoint Set Union.

We will consider $$$dp[j][w]$$$, which denotes the number of ranges that contain the $$$j$$$ node in connection by the triplets/ranges with $$$w$$$ as $$$d$$$ and $$$j$$$ is not $$$a\ +\ k\ *\ d$$$, and $$$id[j][w]$$$, which denotes the node that represents an overall connected component of which $$$j$$$ node is part of for now.

The size of both $$$dp$$$ and $$$id$$$ is $$$max_j * max_w = (n) * 10 = 10\ n$$$.

We will maintain two other arrays, $$$Start_cnt[j][w]$$$ and $$$End_cnt[j][w]$$$, which store the number of triplets with $$$j$$$ as $$$a_i$$$ and $$$a_i+k_i*d_i$$$, respectively, and with $$$w$$$ as $$$d_i$$$, to help us maintain the beginning and end of ranges.

We will now apply Disjoint Set Union. For each $$$i$$$th triplet, we assume $$$a_i$$$ will be the parent node of the Set created by $$$a_i$$$, $$$a_i$$$ + $$$d_i$$$, ..., $$$a_i+k_i*d_i$$$.

The transitions of $$$dp$$$ are as follows:

1) if $$$j \ge 10$$$ (max of $$$d_i$$$): for all $$$w$$$, $$$dp[j][w]$$$ are the same as $$$dp[j-w][w]$$$, just with some possible changes. These changes are due to $$$j$$$ being the start or the end of some triplet with $$$d_i$$$ as $$$w.$$$ So, let us start with $$$dp[j][w]$$$ as $$$Start_cnt[j][w] - End_cnt[j][w]$$$. If $$$dp[j-w][w]$$$ is non-zero, then perform a union operation (of DSU) between the $$$j$$$ node and $$$id[j-w][w]$$$, increment $$$dp[j][w]$$$ by $$$dp[j-w][w]$$$, and assign $$$id[j][w]$$$ as $$$id[j-w][w]$$$. This unites the ranges over the $$$j$$$ node.

2) if $$$j \lt 10$$$ (max of $$$d_i$$$): we do the same as above; rather than doing for all $$$w,$$$ we would restrict ourselves with $$$w$$$ from $$$0$$$ to $$$j-1$$$.

The net time complexity = updation of $$$dp[j][w]$$$ value by $$$Start_cnt$$$ and $$$End_cnt$$$ + union operations due to union of $$$id[j-w][w]$$$ with $$$j$$$ over all $$$w$$$ + incrementing $$$dp$$$ values (by $$$dp[j-w][w]$$$) + copying $$$id$$$ values = $$$10\ n + 10\ nlogn + 10\ n + 10\ n= 10 nlogn + 30n$$$ (in worst case) = $$$O(max_d*n*logn)$$$.

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 2e5+2;
const ll C = 10 + 1;
 
vector<ll> par(N), sz(N, 0);
vector<vector<ll>> dp(N, vector<ll> (C, 0)), ind(N, vector<ll> (C, 0)), start_cnt(N, vector<ll> (C, 0)), end_cnt(N, vector<ll> (C,0));
 
ll find_par(ll a) {
    if (par[a] == a) return a;
    return par[a] = find_par(par[a]);
}
 
void unite(ll a, ll b){
    a = find_par(a), b = find_par(b);
    if (a == b) return;
    if (sz[b] > sz[a]) swap(a, b);
    sz[a] += sz[b];
    par[b] = a;
}
 
void reset(ll n) {
    for (ll i = 1; i <= n; i++) {
        par[i] = i;
        sz[i] = 1;
        for (ll j = 1; j < C; j++) {
            dp[i][j] = start_cnt[i][j] = end_cnt[i][j] = 0;
            ind[i][j] = i;
        }
    }
}
 
void solve() {
    ll n, m, a, d, k;
    cin >> n >> m;
    reset(n);
    for (ll i = 0; i < m; i++) {
        cin >> a >> d >> k;
        start_cnt[a][d]++;
        end_cnt[a + k * d][d]++;
    }
    for (ll i = 1; i <= n; i++) {
        for (ll j = 1; j < C; j++) {
            dp[i][j] = start_cnt[i][j] - end_cnt[i][j];
            if (i-j < 1) continue;
            if (dp[i-j][j]) {
                unite(ind[i-j][j], i);
                ind[i][j] = ind[i-j][j];
                dp[i][j] += dp[i-j][j];
            }
        }
    }
    ll ans = 0;
    for (ll i = 1; i <= n; i++) {
        if (find_par(i) == i) ans++;
    }
    cout << ans << "\n";
}
 
int main() {
    ll t;
    cin >> t;
    while (t--) {
        solve();
    }
}

Try to find the expected value of $$$f(S)$$$ rather than $$$(f(S))^2$$$.

Write the binary representation of $$$f(S)$$$ and find $$$(f(S))^2$$$.

Let the binary representation of the $$$Power$$$ be $$$b_{20}b_{19}...b_{0}$$$. Now $$$Power^2$$$ is $$$\sum_{i=0}^{20} \sum_{j=0}^{20} b_i b_j * 2^{i+j}$$$. Now if we compute the expected value of $$$b_ib_j$$$ for every pair $$$(i,j)$$$, then we are done.

We can achieve this by dynamic programming. For each pair $$$i,j$$$, there are only 4 possible values of $$$b_i,b_j$$$. For every possible value, we can maintain the probability of reaching it, and we are done.

The complexity of the solution is $$$O(n.log(max(a_i))^2)$$$.

#include <bits/stdc++.h>
using namespace std;
int fast_exp(int b, int e, int mod){
	int ans = 1;
	while(e){
		if(e&1) ans = (1ll*ans*b) % mod;
		b = (1ll*b*b) % mod;
		e >>= 1;
	}
	return ans;
}
const int mod = 1e9+7;
const int bits = 11;
 
int inv(int n){
	return fast_exp(n,mod-2,mod);
}
 
const int inverse_1e4 = inv(10000);
int dp[bits][bits][2][2];
void transition(int a, int p){
	p = (1ll*p*inverse_1e4) % mod;
	int negp = (mod+1-p) % mod;
	int bin[bits];
	for(int i = 0; i < bits; i++){
		bin[i] = a&1;
		a >>= 1;
	}
	for(int i = 0; i < bits; i++){
		for(int j = 0; j < bits; j++){
			int temp[2][2];
 
			for(int k : {0,1}) for(int l : {0,1}) temp[k][l] = (1ll*dp[i][j][k][l]*negp + 1ll*dp[i][j][k^bin[i]][l^bin[j]]*p) % mod;
 
			for(int k : {0,1}) for(int l : {0,1}) dp[i][j][k][l] = temp[k][l];
		}
	}
}
int main() {
    int t;
    cin >> t;
    while(t--){
    	int n;
    	cin >> n;
    	int a[n],p[n];
    	for(int i = 0; i < n; i++) cin >> a[i];
    	for(int i = 0; i < n; i++) cin >> p[i];
    	for(int i = 0; i < bits; i++) for(int j = 0; j < bits; j++) dp[i][j][0][0] = 1;
    	for(int i = 0; i < n; i++) transition(a[i],p[i]);
    	int ans = 0;
    	for(int i = 0; i < bits; i++){
    		for(int j = 0; j < bits; j++){
    			int pw2 = (1ll<<(i+j)) % mod;
    			ans += (1ll*pw2*dp[i][j][1][1]) % mod;
    			ans %= mod;
    			for(int k : {0,1}) for(int l : {0,1}) dp[i][j][k][l] = 0;
    		}
    	}
    	cout << ans << "\n";
    }
	return 0;
}

$$$f$$$ satisfies a special property for fixed d.

It can be observed that the number of leaves is equal to the number of ways of choosing $$$d$$$ integers $$$a_0,a_1,a_2...a_d$$$ with $$$a_d = n$$$ and $$$a_i divides a_{i+1}$$$ for all $$$(0 \le i \le d-1)$$$.

Lets define $$$g(n) = f(n,d)$$$ for given $$$d$$$. It can be seen that the function $$$g$$$ is multiplicative i.e. $$$g(p*q) = g(p)*g(q)$$$ if $$$p$$$ and $$$q$$$ are coprime.

Now, lets try to calculate $$$g(n)$$$ when $$$n$$$ is of the form $$$p^x$$$ where $$$p$$$ is a prime number and $$$x$$$ is any non negative integer. From the first observation, we can say that here all the $$$a_i$$$ will be a power of $$$p$$$. Therefore $$$a_0,a_1,a_2...a_d$$$ can be written as $$$p^{b_0},p^{b_1},p^{b_2}...p^{b_d}$$$. Now we just have to ensure that $$$0 \le b_0 \le b_1 \le b_2 ... \le b_d = x$$$. The number of ways of doing so is $$$\binom{x+d}{d}$$$.

Now, lets make a dp (inspired by the idea of the dp used in fast prime counting) where $$$dp(n,x) = \sum_{i=1, spf(i) \gt = x}^{n} g(i)$$$. Here $$$spf(i)$$$ means smallest prime factor of $$$i$$$.

Our required answer is $$$dp(n,2)$$$.

The overall complexity of the solution is $$$O(n^{\frac{2}{3}})$$$.

#include <bits/stdc++.h>
#define ll long long
#define pb push_back
#define mp make_pair
#define F first
#define S second
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pcc pair<char,char>
#define vi vector <int>
#define vl vector <ll>
#define sd(x) scanf("%d",&x)
#define slld(x) scanf("%lld",&x)
#define pd(x) printf("%d",x)
#define plld(x) printf("%lld",x)
#define pds(x) printf("%d ",x)
#define pllds(x) printf("%lld ",x)
#define pdn(x) printf("%d\n",x)
#define plldn(x) printf("%lld\n",x)
using namespace std;
ll powmod(ll base,ll exponent,ll mod){
	ll ans=1;
	if(base<0) base+=mod;
	while(exponent){
		if(exponent&1)ans=(ans*base)%mod;
		base=(base*base)%mod;
		exponent/=2;
	}
	return ans;
}
ll gcd(ll a, ll b){
	if(b==0) return a;
	else return gcd(b,a%b);
}
const int INF = 2e9;
const ll INFLL = 4e18;
const int small_lim = 1e6+1;
const int mod = 1e9+7;
const int big_lim = 1e3+1;
ll primes_till_i[small_lim];
ll primes_till_bigger_i[big_lim];
vl sieved_primes[small_lim];
vl sieved_primes_big[big_lim];
vi prime;
int N,k,d;
void sieve(){
	vi lpf(small_lim);
	ll pw;
	for(int i = 2; i < small_lim; i++){
		if(! lpf[i]){
			prime.pb(i);
			lpf[i] = i;
		}
		for(int j : prime){
			if((j > lpf[i]) || (j*i >= small_lim)) break;
			lpf[j*i] = j;
		}
	}
	for(int i = 2; i < small_lim; i++){
		primes_till_i[i] = primes_till_i[i-1] + (lpf[i] == i);
	}
}
ll count_primes(ll n, int ind){
	if(ind < 0) return n-1;
	if(1ll*prime[ind]*prime[ind] > n){
		if(n < small_lim) return primes_till_i[n];
		if(primes_till_bigger_i[N/n]) return primes_till_bigger_i[N/n];
		int l = -1, r = ind;
		while(r-l > 1){
			int mid = (l+r)>>1;
			if(1ll*prime[mid]*prime[mid] > n) r = mid;
			else l = mid;
		}
		return primes_till_bigger_i[N/n] = count_primes(n,l);
	}
	int sz;
	if(n < small_lim) sz = sieved_primes[n].size();
	else sz = sieved_primes_big[N/n].size();
	ll ans;
	if(sz <= ind){
		ans = count_primes(n,ind-1);
		ans -= count_primes(n/prime[ind],ind-1);
		ans += ind;
		if(n < small_lim) sieved_primes[n].pb(ans);
		else sieved_primes_big[N/n].pb(ans);
	}
	if(n < small_lim) return sieved_primes[n][ind];
	else return sieved_primes_big[N/n][ind];
}
ll count_primes(ll n){
	if(n < small_lim) return primes_till_i[n];
	if(primes_till_bigger_i[N/n]) return primes_till_bigger_i[N/n];
	return count_primes(n,prime.size()-1);
}
 
const int ncrlim = 3.5e6;
 
int fact[ncrlim];
int invfact[ncrlim];
 
void init_fact(){
	fact[0] = 1;
	for(int i = 1; i < ncrlim; i++) fact[i] = (1ll*fact[i-1]*i)%mod;
	invfact[ncrlim-1] = powmod(fact[ncrlim-1], mod-2, mod);
	for(int i = ncrlim-1; i > 0; i--) invfact[i-1] = (1ll*invfact[i]*i)%mod;
}
 
int ncr(int n, int r){
	if(r > n || r < 0) return 0;
	int ans = fact[n];
	ans = (1ll*ans*invfact[n-r]) % mod;
	ans = (1ll*ans*invfact[r]) % mod;
	return ans;
}
 
ll calculate_dp(ll n, int ind){
	if(n == 0) return 0;
	if(prime[ind] > n) return 1;
	ll ans = 1,temp;
	if(1ll*prime[ind]*prime[ind] > n){
		temp = ncr(k+d,d);
		temp *= count_primes(n)-ind;
		ans+=temp; ans %= mod;
		return ans;
	}
	ans = 0;
	ll gg = 1;
	ll mult = d;
	while(gg <= n){
		temp = calculate_dp(n/gg,ind+1);
		temp *= ncr(mult,d);
		ans += temp;
		ans %= mod;
		mult += k;
		gg *= prime[ind];
	}
	return ans;
}
int main(){
	sieve();
	init_fact();
	int t;
	sd(t);
	while(t--){
		sd(N);sd(k);sd(d);
		plldn(calculate_dp(N,0));
		for(int i = 1; i < big_lim; i++){
			primes_till_bigger_i[i] = 0;
			sieved_primes_big[i].clear();
		}
	}
	return 0;
}