A. Find Min Operations
By nishkarsh
How many operations will have $$$x = 0$$$.
Try $$$k = 2$$$.
Answer will be the number of ones in binary representation of $$$n$$$.
If $$$k$$$ is 1, we can only subtract 1 in each operation, and our answer will be $$$n$$$.
Now, first, it can be seen that we have to apply at least $$$n$$$ mod $$$k$$$ operations of subtracting $$$k^0$$$ (as all the other operations will not change the value of $$$n$$$ mod $$$k$$$). Now, once $$$n$$$ is divisible by $$$k$$$, solving the problem for $$$n$$$ is equivalent to solving the problem for $$$\frac{n}{k}$$$ as subtracting $$$k^0$$$ will be useless because if we apply the $$$k^0$$$ subtraction operation, then $$$n$$$ mod $$$k$$$ becomes $$$k-1$$$, and we have to apply $$$k-1$$$ more operations to make $$$n$$$ divisible by $$$k$$$ (as the final result, i.e., 0 is divisible by $$$k$$$). Instead of doing these $$$k$$$ operations of subtracting $$$k^0$$$, a single operation subtracting $$$k^1$$$ will do the job.
So, our final answer becomes the sum of the digits of $$$n$$$ in base $$$k$$$.
The complexity of the solution is $$$O(\log_{k}{n})$$$ per testcase.
#include <bits/stdc++.h>
using namespace std;
int find_min_oper(int n, int k){
if(k == 1) return n;
int ans = 0;
while(n){
ans += n%k;
n /= k;
}
return ans;
}
int main()
{
int t;
cin >> t;
while(t--){
int n,k;
cin >> n >> k;
cout << find_min_oper(n,k) << "\n";
}
return 0;
}
B. Brightness Begins
By nishkarsh
The final state of $$$i$$$th bulb (on or off) is independent of $$$n$$$.
The final state of the $$$i$$$th bulb tells us about the parity of number of divisors of $$$i$$$.
For any bulb $$$i$$$, its final state depends on the parity of the number of divisors of $$$i$$$. If $$$i$$$ has an even number of divisors, then bulb $$$i$$$ will be on; else it will be off. This translates to, if $$$i$$$ is not a perfect square, bulb $$$i$$$ will be on; else it will be off. So now the problem is to find the $$$k$$$th number which is not a perfect square. This can be done by binary searching the value of $$$n$$$ such that $$$n- \lfloor \sqrt{n} \rfloor = k$$$ or the direct formula $$$n$$$ = $$$\lfloor k + \sqrt{k} + 0.5 \rfloor$$$.
For the proof of the second formula you can refer this book page 141 E18
#include <bits/stdc++.h>
using namespace std;
int main(){
int t;
cin >> t;
while(t--){
long long k, l = 1, r = 2e18;
cin >> k;
while(r-l > 1){
long long mid = (l+r)>>1;
long long n = mid - int(sqrtl(mid));
if(n >= k) r = mid;
else l = mid;
}
cout << r << "\n";
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main(){
int t;
cin >> t;
while(t--){
long long k;
cin >> k;
cout << k + int(sqrtl(k) + 0.5) << "\n";
}
return 0;
}
C. Bitwise Balancing
By P.V.Sekhar
Try to find some independent operations/combinations.
The expression is independent for each digit in binary representation
The first observation is that the expression $$$a$$$|$$$b$$$ - $$$a$$$&$$$c = d$$$ is bitwise independent. That is, the combination of a tuple of bits of $$$a, b, and\ c$$$ corresponding to the same power of 2 will only affect the bit value of $$$d$$$ at that power of 2 only.
This is because:
We are performing subtraction, so extra carry won't be generated to the next power of 2.
Any tuple of bits of $$$a$$$, $$$b$$$, and $$$c$$$ corresponding to the same power of 2 won't result in -1 for that power of 2. As that would require $$$a|b$$$ to be zero and $$$a$$$&$$$c$$$ to be one. The former condition requires the bit of $$$a$$$ to be zero, while the latter requires it to be one, which is contradicting.
Now, let us consider all 8 cases of bits of a, b, c and the corresponding bit value of d in the following table:
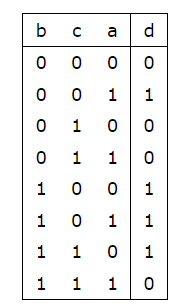
So, clearly, for different bits of $$$b, c,$$$ and $$$d$$$, we can find the value of the corresponding bit in $$$a$$$, provided it is not the case when bit values of $$$b, c,$$$ and $$$d$$$ are 1,0,0 or 0,1,1, which are not possible; so, in that case, the answer is -1.
#include <bits/stdc++.h>
#define ll long long
using namespace std;
void solve() {
ll a = 0, b, c, d, pos = 1, bit_b, bit_c, bit_d, mask = 1;
cin >> b >> c >> d;
for (ll i = 0; i < 62; i++) {
if (b&mask) bit_b = 1;
else bit_b = 0;
if (c&mask) bit_c = 1;
else bit_c = 0;
if (d&mask) bit_d = 1;
else bit_d = 0;
if ((bit_b && (!bit_c) && (!bit_d)) || ((!bit_b) && bit_c && bit_d)) {
pos = 0;
break;
}
if (bit_b && bit_c) {
a += (1ll-bit_d)*mask;
} else {
a += bit_d*mask;
}
mask<<=1;
}
if (pos) {
cout << a << "\n";
} else {
cout << -1 << "\n";
}
}
int main() {
ll t;
cin >> t;
while (t--) {
solve();
}
}
D. Connect the Dots
By P.V.Sekhar
The value of $$$d$$$ is very small.
Try using Disjoint Set Union (DSU).
The main idea is to take advantage of the low upper bound of $$$d_i$$$ and apply the Disjoint Set Union.
We will consider $$$dp[j][w]$$$, which denotes the number of ranges that contain the $$$j$$$ node in connection by the triplets/ranges with $$$w$$$ as $$$d$$$ and $$$j$$$ is not $$$a\ +\ k\ *\ d$$$, and $$$id[j][w]$$$, which denotes the node that represents an overall connected component of which $$$j$$$ node is part of for now.
The size of both $$$dp$$$ and $$$id$$$ is $$$max_j * max_w = (n) * 10 = 10\ n$$$.
We will maintain two other arrays, $$$Start_cnt[j][w]$$$ and $$$End_cnt[j][w]$$$, which store the number of triplets with $$$j$$$ as $$$a_i$$$ and $$$a_i+k_i*d_i$$$, respectively, and with $$$w$$$ as $$$d_i$$$, to help us maintain the beginning and end of ranges.
We will now apply Disjoint Set Union. For each $$$i$$$th triplet, we assume $$$a_i$$$ will be the parent node of the Set created by $$$a_i$$$, $$$a_i$$$ + $$$d_i$$$, ..., $$$a_i+k_i*d_i$$$.
The transitions of $$$dp$$$ are as follows:
1) if $$$j \ge 10$$$ (max of $$$d_i$$$): for all $$$w$$$, $$$dp[j][w]$$$ are the same as $$$dp[j-w][w]$$$, just with some possible changes. These changes are due to $$$j$$$ being the start or the end of some triplet with $$$d_i$$$ as $$$w.$$$ So, let us start with $$$dp[j][w]$$$ as $$$Start_cnt[j][w] - End_cnt[j][w]$$$. If $$$dp[j-w][w]$$$ is non-zero, then perform a union operation (of DSU) between the $$$j$$$ node and $$$id[j-w][w]$$$, increment $$$dp[j][w]$$$ by $$$dp[j-w][w]$$$, and assign $$$id[j][w]$$$ as $$$id[j-w][w]$$$. This unites the ranges over the $$$j$$$ node.
2) if $$$j \lt 10$$$ (max of $$$d_i$$$): we do the same as above; rather than doing for all $$$w,$$$ we would restrict ourselves with $$$w$$$ from $$$0$$$ to $$$j-1$$$.
The net time complexity = updation of $$$dp[j][w]$$$ value by $$$Start_cnt$$$ and $$$End_cnt$$$ + union operations due to union of $$$id[j-w][w]$$$ with $$$j$$$ over all $$$w$$$ + incrementing $$$dp$$$ values (by $$$dp[j-w][w]$$$) + copying $$$id$$$ values = $$$10\ n + 10\ nlogn + 10\ n + 10\ n= 10 nlogn + 30n$$$ (in worst case) = $$$O(max_d*n*logn)$$$.
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 2e5+2;
const ll C = 10 + 1;
vector<ll> par(N), sz(N, 0);
vector<vector<ll>> dp(N, vector<ll> (C, 0)), ind(N, vector<ll> (C, 0)), start_cnt(N, vector<ll> (C, 0)), end_cnt(N, vector<ll> (C,0));
ll find_par(ll a) {
if (par[a] == a) return a;
return par[a] = find_par(par[a]);
}
void unite(ll a, ll b){
a = find_par(a), b = find_par(b);
if (a == b) return;
if (sz[b] > sz[a]) swap(a, b);
sz[a] += sz[b];
par[b] = a;
}
void reset(ll n) {
for (ll i = 1; i <= n; i++) {
par[i] = i;
sz[i] = 1;
for (ll j = 1; j < C; j++) {
dp[i][j] = start_cnt[i][j] = end_cnt[i][j] = 0;
ind[i][j] = i;
}
}
}
void solve() {
ll n, m, a, d, k;
cin >> n >> m;
reset(n);
for (ll i = 0; i < m; i++) {
cin >> a >> d >> k;
start_cnt[a][d]++;
end_cnt[a + k * d][d]++;
}
for (ll i = 1; i <= n; i++) {
for (ll j = 1; j < C; j++) {
dp[i][j] = start_cnt[i][j] - end_cnt[i][j];
if (i-j < 1) continue;
if (dp[i-j][j]) {
unite(ind[i-j][j], i);
ind[i][j] = ind[i-j][j];
dp[i][j] += dp[i-j][j];
}
}
}
ll ans = 0;
for (ll i = 1; i <= n; i++) {
if (find_par(i) == i) ans++;
}
cout << ans << "\n";
}
int main() {
ll t;
cin >> t;
while (t--) {
solve();
}
}
E. Expected Power
By nishkarsh
Try to find the expected value of $$$f(S)$$$ rather than $$$(f(S))^2$$$.
Write the binary representation of $$$f(S)$$$ and find $$$(f(S))^2$$$.
Let the binary representation of the $$$Power$$$ be $$$b_{20}b_{19}...b_{0}$$$. Now $$$Power^2$$$ is $$$\sum_{i=0}^{20} \sum_{j=0}^{20} b_i b_j * 2^{i+j}$$$. Now if we compute the expected value of $$$b_ib_j$$$ for every pair $$$(i,j)$$$, then we are done.
We can achieve this by dynamic programming. For each pair $$$i,j$$$, there are only 4 possible values of $$$b_i,b_j$$$. For every possible value, we can maintain the probability of reaching it, and we are done.
The complexity of the solution is $$$O(n.log(max(a_i))^2)$$$.
#include <bits/stdc++.h>
using namespace std;
int fast_exp(int b, int e, int mod){
int ans = 1;
while(e){
if(e&1) ans = (1ll*ans*b) % mod;
b = (1ll*b*b) % mod;
e >>= 1;
}
return ans;
}
const int mod = 1e9+7;
const int bits = 11;
int inv(int n){
return fast_exp(n,mod-2,mod);
}
const int inverse_1e4 = inv(10000);
int dp[bits][bits][2][2];
void transition(int a, int p){
p = (1ll*p*inverse_1e4) % mod;
int negp = (mod+1-p) % mod;
int bin[bits];
for(int i = 0; i < bits; i++){
bin[i] = a&1;
a >>= 1;
}
for(int i = 0; i < bits; i++){
for(int j = 0; j < bits; j++){
int temp[2][2];
for(int k : {0,1}) for(int l : {0,1}) temp[k][l] = (1ll*dp[i][j][k][l]*negp + 1ll*dp[i][j][k^bin[i]][l^bin[j]]*p) % mod;
for(int k : {0,1}) for(int l : {0,1}) dp[i][j][k][l] = temp[k][l];
}
}
}
int main() {
int t;
cin >> t;
while(t--){
int n;
cin >> n;
int a[n],p[n];
for(int i = 0; i < n; i++) cin >> a[i];
for(int i = 0; i < n; i++) cin >> p[i];
for(int i = 0; i < bits; i++) for(int j = 0; j < bits; j++) dp[i][j][0][0] = 1;
for(int i = 0; i < n; i++) transition(a[i],p[i]);
int ans = 0;
for(int i = 0; i < bits; i++){
for(int j = 0; j < bits; j++){
int pw2 = (1ll<<(i+j)) % mod;
ans += (1ll*pw2*dp[i][j][1][1]) % mod;
ans %= mod;
for(int k : {0,1}) for(int l : {0,1}) dp[i][j][k][l] = 0;
}
}
cout << ans << "\n";
}
return 0;
}
F. Count Leaves
By nishkarsh
$$$f$$$ satisfies a special property for fixed d.
$$$f$$$ is multiplicative i.e. $$$f(x.y)$$$ = $$$f(x) * f(y)$$$ if $$$x,y$$$ are coprime, for fixed d.
It can be observed that the number of leaves is equal to the number of ways of choosing $$$d$$$ integers $$$a_0,a_1,a_2...a_d$$$ with $$$a_d = n$$$ and $$$a_i divides a_{i+1}$$$ for all $$$(0 \le i \le d-1)$$$.
Lets define $$$g(n) = f(n,d)$$$ for given $$$d$$$. It can be seen that the function $$$g$$$ is multiplicative i.e. $$$g(p*q) = g(p)*g(q)$$$ if $$$p$$$ and $$$q$$$ are coprime.
Now, lets try to calculate $$$g(n)$$$ when $$$n$$$ is of the form $$$p^x$$$ where $$$p$$$ is a prime number and $$$x$$$ is any non negative integer. From the first observation, we can say that here all the $$$a_i$$$ will be a power of $$$p$$$. Therefore $$$a_0,a_1,a_2...a_d$$$ can be written as $$$p^{b_0},p^{b_1},p^{b_2}...p^{b_d}$$$. Now we just have to ensure that $$$0 \le b_0 \le b_1 \le b_2 ... \le b_d = x$$$. The number of ways of doing so is $$$\binom{x+d}{d}$$$.
Now, lets make a dp (inspired by the idea of the dp used in fast prime counting) where $$$dp(n,x) = \sum_{i=1, spf(i) >= x}^{n} g(i)$$$. Here $$$spf(i)$$$ means smallest prime factor of $$$i$$$.
Our required answer is $$$dp(n,2)$$$.
The overall complexity of the solution is $$$O(n^{\frac{2}{3}})$$$.
#include <bits/stdc++.h>
#define ll long long
#define pb push_back
#define mp make_pair
#define F first
#define S second
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pcc pair<char,char>
#define vi vector <int>
#define vl vector <ll>
#define sd(x) scanf("%d",&x)
#define slld(x) scanf("%lld",&x)
#define pd(x) printf("%d",x)
#define plld(x) printf("%lld",x)
#define pds(x) printf("%d ",x)
#define pllds(x) printf("%lld ",x)
#define pdn(x) printf("%d\n",x)
#define plldn(x) printf("%lld\n",x)
using namespace std;
ll powmod(ll base,ll exponent,ll mod){
ll ans=1;
if(base<0) base+=mod;
while(exponent){
if(exponent&1)ans=(ans*base)%mod;
base=(base*base)%mod;
exponent/=2;
}
return ans;
}
ll gcd(ll a, ll b){
if(b==0) return a;
else return gcd(b,a%b);
}
const int INF = 2e9;
const ll INFLL = 4e18;
const int small_lim = 1e6+1;
const int mod = 1e9+7;
const int big_lim = 1e3+1;
ll primes_till_i[small_lim];
ll primes_till_bigger_i[big_lim];
vl sieved_primes[small_lim];
vl sieved_primes_big[big_lim];
vi prime;
int N,k,d;
void sieve(){
vi lpf(small_lim);
ll pw;
for(int i = 2; i < small_lim; i++){
if(! lpf[i]){
prime.pb(i);
lpf[i] = i;
}
for(int j : prime){
if((j > lpf[i]) || (j*i >= small_lim)) break;
lpf[j*i] = j;
}
}
for(int i = 2; i < small_lim; i++){
primes_till_i[i] = primes_till_i[i-1] + (lpf[i] == i);
}
}
ll count_primes(ll n, int ind){
if(ind < 0) return n-1;
if(1ll*prime[ind]*prime[ind] > n){
if(n < small_lim) return primes_till_i[n];
if(primes_till_bigger_i[N/n]) return primes_till_bigger_i[N/n];
int l = -1, r = ind;
while(r-l > 1){
int mid = (l+r)>>1;
if(1ll*prime[mid]*prime[mid] > n) r = mid;
else l = mid;
}
return primes_till_bigger_i[N/n] = count_primes(n,l);
}
int sz;
if(n < small_lim) sz = sieved_primes[n].size();
else sz = sieved_primes_big[N/n].size();
ll ans;
if(sz <= ind){
ans = count_primes(n,ind-1);
ans -= count_primes(n/prime[ind],ind-1);
ans += ind;
if(n < small_lim) sieved_primes[n].pb(ans);
else sieved_primes_big[N/n].pb(ans);
}
if(n < small_lim) return sieved_primes[n][ind];
else return sieved_primes_big[N/n][ind];
}
ll count_primes(ll n){
if(n < small_lim) return primes_till_i[n];
if(primes_till_bigger_i[N/n]) return primes_till_bigger_i[N/n];
return count_primes(n,prime.size()-1);
}
const int ncrlim = 3.5e6;
int fact[ncrlim];
int invfact[ncrlim];
void init_fact(){
fact[0] = 1;
for(int i = 1; i < ncrlim; i++) fact[i] = (1ll*fact[i-1]*i)%mod;
invfact[ncrlim-1] = powmod(fact[ncrlim-1], mod-2, mod);
for(int i = ncrlim-1; i > 0; i--) invfact[i-1] = (1ll*invfact[i]*i)%mod;
}
int ncr(int n, int r){
if(r > n || r < 0) return 0;
int ans = fact[n];
ans = (1ll*ans*invfact[n-r]) % mod;
ans = (1ll*ans*invfact[r]) % mod;
return ans;
}
ll calculate_dp(ll n, int ind){
if(n == 0) return 0;
if(prime[ind] > n) return 1;
ll ans = 1,temp;
if(1ll*prime[ind]*prime[ind] > n){
temp = ncr(k+d,d);
temp *= count_primes(n)-ind;
ans+=temp; ans %= mod;
return ans;
}
ans = 0;
ll gg = 1;
ll mult = d;
while(gg <= n){
temp = calculate_dp(n/gg,ind+1);
temp *= ncr(mult,d);
ans += temp;
ans %= mod;
mult += k;
gg *= prime[ind];
}
return ans;
}
int main(){
sieve();
init_fact();
int t;
sd(t);
while(t--){
sd(N);sd(k);sd(d);
plldn(calculate_dp(N,0));
for(int i = 1; i < big_lim; i++){
primes_till_bigger_i[i] = 0;
sieved_primes_big[i].clear();
}
}
return 0;
}










whats the point of allowing $$$O(n \cdot 1024)$$$ solutions in E
well, we reduced the bound on A to make sure nlog^2A passes.
We didn't knew that these solutions existed.
know*
I think $$$a_i < 2^{14}$$$ or something would've been the optimal choice if i am not mistaken $$$O(n \log^2 A)$$$ should pass as long as there is no bad constant factor and the more naive solution wouldn't have passed but i am sure it was hard to predict that such solutions would pop up + thanks for the amazing contest.
It's not hard to expect that the dp 1024n is too easy and obvious to anyone who has solved dp+ev before
Yes it is straight forward but $$$n$$$ is still upto $$$2 \cdot 10^5$$$ so passing shouldn't seem smooth, some people even got TLE.
What is amazing about this contest?
then you just killed the problem
my O(n * 1024) solution passed (4000ms), so I optimized to O(min(n, 1024) * 1024) and it passed 2500ms.
This also didn't seem intended but yeah this solution also exists and it runs in $$$O(\text{max } a_i^2)$$$.
can you please explain your optimized solution for problem E?
Sure. Here’s how I came up with the optimization:
n > 2^10, we have duplicates.2^10):pdp[i][0]— the probability of getting valueian even number of times.pdp[i][1]— the probability of getting it an odd number of times.Dp base for each number = {1, 0} (100% chance of getting zero times).
i(with probpi), we have two transitions:pdp[i] = { pdp[i][0] * (1-pi) + pdp[i][1] * pi, pdp[i][0] * pi + pdp[i][1] * (1-pi) }. I hope these transitions are clear to understand.O(n * 1024), but instead of iterating over alla[i], we will iterate only over unique a[i]. Instead ofp[i], use previously calculated probability dpprob_dp[a[i]]for calculating the new dp. Two transitions: if we take an even number ofa[i]or an odd number ofa[i].My solution (rust): https://mirror.codeforces.com/contest/2020/submission/283652607 In my case
cntarray ispdpprecalculations.Understood, thanks!
Getting tle with the same Approach :((
Can you check it once link : https://mirror.codeforces.com/contest/2020/submission/283786350
Thanks
it is still O(n*1024) ?
I came up with that solution at my first look at E after solving C, but $$$O(n⋅1024)$$$ would definitely TLE, and I couldn't improve my approach. It kinda makes me feel sad to know that such were ACed now :)
283614074 Brute force solution runs 0.9s. Much less than Time Limit 4s, and quite close to official solution which runs 0.7s. When I come to the problem, I get the idea same as the tutorial. But later I see $$$a_i<1024$$$, so I decide to submit $$$O(1024 \min{\{n, 1024\}})$$$ solution which saves lines of codes.
say n = 1 across test cases , then u can have 2e5 test cases in each loop of 1024 makes the complexity O(1024*t) ryght ?
No. The statement says $$$t \le 10^4$$$, and the worst case is $$$2 \times 10^5 \times 1024$$$, nothing to do with $$$t$$$.
crrct , my point is that O(1024min{n,1024}) solution is not the case ,
I replaced 4 modulo operation with 1 in my solution. And it got passed
yeah, my O(n*1024) passed in 765ms
Can anyone explain how did we get the direct formula in B??
Every number has an even number of factors, except square numbers.
We can prove the first fact by finding a factor a of number n. Then, if n is not a square n/a is another factor of n.
If n is a square, then we double count sqrt(n), as we count n/sqrt(n) and sqrt(n) which are the same value. This leads to an odd number of factors(every other factor + 1).
Using this, if a switch is flipped an even number of times, it returns back to 1. If it flipped an odd number of times, it returns to 0.
what is the explanation of n-sqrt(n)>=k?
sqrt(n) gives how many square numbers are there for n, since squares cant be On we need to subtract them to get total lights on and the RHS is since we need to check if ON is atleast k to get the binary search going.
Check the solution discution on YT.
even divisor ...so it will be on
This does not answer the question which was about how to get the direct formula: $$$n=⌊k+\sqrt{k}+0.5⌋$$$
I personally guess it was a trap for chatgpt
I have created a video solution for Problem B and Problem A on my youtube channel, you can checkout, it's a simple and intuitive solution
Video solution for Problem C
first, few keypoints to keep in mind are: 1) sqrt(1)->1,sqrt(4)->2,sqrt(9)->3,sqrt(6)->2.44.....square root of numbers tells you that how many perfect square where there before that number. for example sqrt(9)=3, so there are total 3 perfect square <=9 which are(1,2,3).similarly sqrt(6)=2.44..round of to 2 perfet squares before 6 which are (1,2).
2)now , according to question we need k ones, so why not lets take n=k(for k ones), now we can say there are total sqrt(k) perfect squares. which means if we take n=k there will be total sqrt(k) which will be zero and rest will be 1. hence to make total number of ones =k we have to add sqrt(k) to n so that we get k ones.
3)example- given k=6. now sqrt(k)=round(2.44)=2. that means total perfect squares before 6 will be 2. that means if we take n=6 then we will get two zeroes and 4 ones i.e 011011 . but according to question we need k=6 ones, hence to add extra 2 ones we do n= k+sqrt(k) i.e n=8 which will give total numbers of one=6 i.e 01101111.
4) note the 0.5 factor is there to compensate for next perfect square we can get as a zero. in case of 8. therefor n=k+sqrt(k)+0.5.
What a beautiful explanation. Now I understood the whole solution.
This was a good round, unless I FST ofc, then it was a horrible round. I think that there should be more problems like this — problems that don't require so much IQ, but $$$do$$$ require coding. These problems are what might be called chill problems.
is 123gjweq2 a social experiment?
Now after seeing the solution of B problem.... I just want to cry ):
I was able to figure out that number of ON bulbs after n operations is related to sqrt(n) but was going in opposite track. Here only perfect squares are off and other are ON.
I understood the binary search solution for problem B. But, I am not able to figure out how direct formula $$$n = \lfloor k + \sqrt{k} +0.5 \rfloor$$$ came. Can anyone please explain it?
dont think abt that farmula number of number of perfect squares<=k and add to k(ie (int)sqrt(k)) now we can only cross atmost one more square in b/w [k,k+(int)sqrt(k)] which is ((int)sqrt(k)+1)^2 check for that and add 1 the farmula given directly checks it mathematically
I did a similar approach but got wrong answer. Mind explaining why? This
i think it has problem with sqrt funcuntion like some times it will give root 4=1.999 so it will become 1 so it is good to check if (r+1)(r+1)=k r++;
I am trying to submit binary search solution but I am receiving WA verdict. Even though it is giving correct answer for that test case in my machine. Can you please check what is the problem? https://mirror.codeforces.com/contest/2020/submission/283696903
Thanks
i think its the same problem with you the sqrt funcuntion gives error at intigers some times
Oh I see, these type of arithmetic errors are really difficult to catch unless you know them beforehand. Thanks a lot Veda_2005
Suppose $$$\lfloor \sqrt n \rfloor = m$$$, $$$m^2 < n < (m+1)^2$$$ (note that n wouldn't be a square, as the square lightbulb itself is closed)
So, $$$m^2-m < k < m^2+m+1, m-0.5 < \sqrt k < m+0.5$$$ (inequality is true as k is an integer)
$$$\lfloor \sqrt k +0.5 \rfloor = m = \lfloor \sqrt n \rfloor$$$, $$$ n = k + \lfloor \sqrt k +0.5 \rfloor$$$
Ok, no I understood this formula completely. But, I am not able to understand only this fact that if $$$m^2 - m < k < m^2 + m + 1$$$, then how inequality $$$m - 0.5 < \sqrt{k} < m + 0.5$$$ is true when $$$k$$$ is an integer.
And, I suppose that there is a typo. It should be $$$\lfloor \sqrt{k} + 0.5 \rfloor = m = \lfloor \sqrt{n} \rfloor$$$, instead of $$$\lfloor \sqrt{k} + 0.5 \rfloor = m = \lfloor n \rfloor$$$
Yes the last one is a typo, fixed. $$$m^2-m < (m^2-m+1/4) = (m-0.5)^2 < k < (m+0.5)^2 = m^2+m+1/4 < m^2+m+1$$$
As you can see, 1/4 is added for lower bound, 3/4 is removed for upper bound, so the inequality only works because k is a positive integer.
Ok, now I understood this formula. I as just getting confused why only 0.5 constant is used and not any other number. Thanks a lot TanJWcode
Because the upper bound and lower bound is $$$m^2 \pm m$$$, completing the square gives us the constant. $$$(m+a)^2 = m^2+2am+a^2$$$, here $$$2a= \pm 1$$$
If you're still confused, note that this is a derivation. I'm intentionally deriving $$$n=k+ \lfloor \sqrt k +0.5 \rfloor$$$ from $$$n-\lfloor \sqrt n \rfloor = k$$$
Some parts of the proof is forced, and there are more natural ways of finding the formula
Intuition:
Suppose $$$l^2 \leq k < (l+1)^2$$$, we need at least $$$l$$$ more lights to compensate for the $$$l$$$ squares before $$$k$$$.
As $$$k+l < l^2+3l+1 < l^2+4l+4 = (l+2)^2$$$, there will be at most 1 square between $$$k$$$ and $$$k+l$$$, and we need to add 1 more light if there is one.
So if $$$k+l \geq (l+1)^2, n=k+l+1$$$, else $$$n=k+l$$$ . This already is the solution, 0.5 is added to make the solution into a pretty formula
If $$$k+l \geq (l+1)^2 , k \geq l^2+l+1 > l^2+l+0.25$$$, then $$$\sqrt k > l+0.5$$$
This means if $$$\sqrt k > l+0.5, n=k+l+1$$$, otherwise $$$n=k+l$$$. The formula follows.
first, few keypoints to keep in mind are: 1) sqrt(1)->1,sqrt(4)->2,sqrt(9)->3,sqrt(6)->2.44.....square root of numbers tells you that how many perfect square where there before that number. for example sqrt(9)=3, so there are total 3 perfect square <=9 which are(1,2,3).similarly sqrt(6)=2.44..round of to 2 perfet squares before 6 which are (1,2).
2)now , according to question we need k ones, so why not lets take n=k(for k ones), now we can say there are total sqrt(k) perfect squares. which means if we take n=k there will be total sqrt(k) which will be zero and rest will be 1. hence to make total number of ones =k we have to add sqrt(k) to n so that we get k ones.
3)example- given k=6. now sqrt(k)=round(2.44)=2. that means total perfect squares before 6 will be 2. that means if we take n=6 then we will get two zeroes and 4 ones i.e 011011 . but according to question we need k=6 ones, hence to add extra 2 ones we do n= k+sqrt(k) i.e n=8 which will give total numbers of one=6 i.e 01101111.
4) note the 0.5 factor is there to compensate for next perfect square we can get as a zero. in case of 8. therefor n=k+sqrt(k)+0.5.
Thanks dohcradam for this explanation. I got it now.
In problem B, how do we derive the formula $$$( n = \left\lfloor k + \sqrt{k} + 0.5 \right\rfloor )$$$ from the equation $$$( n - \left\lfloor \sqrt{n} \right\rfloor = k )$$$?
Derivation:
Suppose $$$\lfloor \sqrt n \rfloor = m$$$, $$$m^2 < n < (m+1)^2$$$ (note that n wouldn't be a square, as the square lightbulb itself is closed)
So, $$$m^2-m < k < m^2+m+1, m-0.5 < \sqrt k < m+0.5$$$ (inequality is true as k is an integer)
$$$\lfloor \sqrt k +0.5 \rfloor = m = \lfloor \sqrt n \rfloor$$$, $$$ n = k + \lfloor \sqrt k +0.5 \rfloor$$$
Intuition:
Suppose $$$l^2 \leq k < (l+1)^2$$$, we have $$$n = k+l$$$, if $$$n \geq (l+1)^2$$$, we have to add 1 to compensate for that new square. So $$$n=k+l$$$ or $$$n=k+l+1$$$
$$$n \geq (l+1)^2 , k \geq l^2+l+1 > l^2+l+0.25, \sqrt k > l+0.5$$$
The formula follows.
I understand the derivation, but I am unsure how $$$m - 0.5 < \sqrt{k} < m + 0.5$$$ follows from the condition $$$m^2 - m < k < m^2 + m + 1$$$.
$$$m^2-m < (m^2-m+1/4) = (m-0.5)^2 < k < (m+0.5)^2 = m^2+m+1/4 < m^2+m+1$$$
As you can see, 1/4 is added for lower bound, 3/4 is removed for upper bound, so the inequality only works because k is a positive integer.
Okay, I got it now. Thanks!
If maxa is sth like 2^20, E will be a good problem. What a pity.
A O(1) solution for C exists: if some solution exists both
b ^ dandc ^ dwill be solutions. This comes from simplifying the truth table.O(1) solution for B exists too
cout << k + (int)sqrtl(k + (int)sqrtl(k)) << endl;I don't think this is O(1) since sqrt is log(n) time complexity
It's considered to be constant in bit complexity, just as how we consider other arithmetic operations to have constant complexity.
Amazing
if a = 1 then a | b = 1 and a & c = c LHS = 1 — c = !c
and if a = 0 then a | b = b and a & c = 0 so LHS = b — 0 = b
a=0 => LHS=b
a=1 => LHS=!c
so for each bit where b != d, we can't have LHS = b, so we are forced to set a = 1, otherwise LHS = b != RHS
and if b = d, then we can simply set a = 0, and a = 1 may also work but no need for this ..
we get a=0 if b=d and a=1 if b!=d, this is xor, so a = b ^ d
and for each bit where !c != d <=> c = d, we are forced to set a = 0 to avoid LHS = !c
, otherwise we can set a = 1,
so a=0 if c=d and a=1 if c differs from d, again xor, a = c ^ d
In problem C simply set a to b xor d and check if it works
I think it should be c xor d.
My submission uses b xor d, not c xor d. I believe both work.
You put image of editorial C to editorial D. By accident I suppose
I got the idea of problem B fast because of 1909E - Multiple Lamps.
Doing what problem B does solves this when $$$n \ge 20$$$.
its an extremely well known riddle, here is a youtube link for n = 100
https://www.youtube.com/watch?v=xwWdBj5WfCo
How was I supposed to solve that B problem, I literally had 0 idea that I will have to build a formulae for that, plus the observation required for the problem isn't normal at all.
Binary search is an alternative solution
Here is how I approached it. First I assumed it to be a dumb problem. And from my past experience and noticing that n and k are not far apart in the samples, and by thinking about prime factorization and number of factors (however I didn't dive into that because I was lazy) I suspect maybe only the first few bulbs are not on. And I printed a table of the first 100 n and k, and quickly realized that k=n-(int)sqrtl(n). Obviously then you may construct some weird formula to do it backwards, but I suddenly came up with binary search and solved it.
I didn't think of establishing a formula when solving this problem, but I found the following pattern by observing the case of n=24: 0110111101111110111111110 Using this rule, the problem is transformed into how many zeros need to be inserted into k ones
contest is too math
In B no need for a formula, you can just binary search for the answer, it only needs that observation
That observation is too much for me, tell me how much more I need to practice in order to get that B always right.
I saw that observation before in blogs but usually you just need practice to get observations fast, if you aren't sure how to practice correctly I think there's lots of cf blogs on it
I personally guess that formula was a trap for chatgpt cheaters
Can someone help me with my code for E. I am finding probability for each bit to be active or not then for all number adding it's contribution to expectation.
z[i][0][j] represent prob in first i element our subset's xor will have j'th bit set
z[i][1][j] represent prob in first i element our subset's xor will not have j'th bit set
then for each number(0-1023) i add contribution number 5's contribution would be simply (z[n-1][0][0]*z[n-1][1][1]*z[n-1][2][0])*5*5
Squaring is not linear so you can't handle bit by bit without doing the editorial's trick, what works is z[i][j] represents probability in first i element that the xor is equal to j
i do understand editorial's way but can't find mistake in my own approch. can you may be give me little example
Oh I didn't understand your solution, it looks like it should work, there might be an implementation mistake somewhere
At first I thought of something similar for this problem. The issue is that the probability of getting a 1 on the ith bit is not independent to the probability of getting a 1 on the jth bit. An example of this may be that given the case:
1
3
5000
I can either take the 2^0 bit and the 2^1 bit or I can take neither, yet your implementation may give some probability to 2's contribution.
Makes sense I think that's the problem with the solution
Ahhh!! you are absolutely right i see problem now.
I had the same idea when implementing at first, but the bit-by-bit approach doesn't work because you're trying to use linearity of expectation on a non-linear operation (squaring). If you're given $$$A=[101_2]$$$ and $$$P=[0.5]$$$, then you should have a 50% chance of obtaining $$$0^2=0$$$ and a 50% chance of obtaining $$$(101_2)^2 = 25$$$. However, if you solve bit-by-bit, your solution will conclude that you have a 25% chance of obtaining $$$(000_2)^2=0$$$, a 25% for $$$(001_2)^2=1$$$, 25% for $$$(100_2)^2=16$$$, and 25% for $$$(101_2)^2=25$$$, which should be impossible since you can only xor by full numbers, not just their individual bits.
Let's say you only have one element in the array, 3. I believe your solution produces a non-zero expected value for the XOR to be 1, because the 0th bit is set in 3. But a XOR value of 1 cannot be achieved.
The editorial solution for E is too complicated. There is a much easier O(1024 * n) dynamic programming solution which comfortably fits within time limit.
Probably it was not intended. But I don't know why they even allowed O(1024n) to pass. Could've had a[i]<10^9 and time limit 4 seconds or something like that
They said they didn't know such solution exists: https://mirror.codeforces.com/blog/entry/134516?#comment-1203470
Why is Carrot not working !?
E can (accidentally) be solved with FWT: https://mirror.codeforces.com/contest/2020/submission/283601247
What is fwt?
fast wavelet transform
https://mirror.codeforces.com/blog/entry/71899 fast walsh hadamard transform
This works, but you can do it more efficiently in $$$O(N + max(A) \cdot log^2(max(A)))$$$ with a divide & conquer approach. Unfortunately it doesn't pass TLs because of high number of test cases: 283681726
Seems like you didnt consider two much easier solutions in D and E
I have solved D using different approach.I won't say it is easy but if someone wants to see here it it 283680740
I solved it with approach that if we fix d and a_i % d, the request is just to merge some vertices inside segment, so its just +1 on segment offline
Problem D has a much easier $$$O(nd^2 + m)$$$ solution.
I solved Problem d using 10 dsu (one for each d).283663343
Hello can anyone help me why B submission is getting WA on Test case 8?
Can anyone tell me what I am doing wrong looking at my profile, I am unable to reach pupil
solve more problems and implement fast!
$$$O(nd+m)$$$ solution to D: 283633809 We can brute force all edges and run dfs for connected components, since there are at most $$$2*d$$$ edges per node.
can u explain how can a node have at most 2*d edges only
For each d and a particular number a, a can only be connected to a-d or a+d.
Can anyone help me debug my code, It failed test case 8. I tried so hard today but not enough :(
Submission:283668245
use sqrtl, because sqrt looses precision with big numbers (i didn't solve B because of that)
I struggled with this as well, until I finally decided to google for "c++ square root of int64" and was able to solve the problem just in time. Then I looked at the tutorial and discovered
sqrtl.Same bro, use isqrt with Python
For C, can someone explain why it is bit independent? I am unable to wrap my head around it
Assume it is not bit independent. Then there must be some i, for which (a|b)'s i-th bit is not set and (a&c)'s i-th bit is set. If (a&c)'s i-th bit is set, then a's i-th bit must also be set. But if a's i-th bit is set, then (a|b)'s i-th set must also be set, which is a contradiction. Therefore it is bit independent.
Oh yes! That makes sense. THANKS!
Also if you can, can you tell why this submission is failing?
283672706
Subtraction in kth bit place in
p - q = raffect other places only if pk is 0 and qk is 1.0 - 0 = 01 - 0 = 11 - 1 = 0For this case to happen, (ak | bk) = 0 which means ak = 0
but (ak & ck) = 1 which means ak = 1 which is a contradiction
Hope the explanation is clear!
This was very helpful, Thanks a lot!
An alternative solution to the problem D in $$$O(max_d * n + m)$$$
Consider the point $$$x$$$, note that it can only be connected to the $$$max_d$$$ points that go in front of it. We will support $$$dp[x][d] = k$$$, where $$$x$$$ is the coordinate of a point on a numeric line, $$$d$$$ is the length of the reverse step, $$$k$$$ is the maximum number of steps that will be taken from point $$$x$$$ with step $$$d$$$. Then note that we can move from point $$$x - d$$$ to point $$$d$$$ only if $$$dp[x - d][d] > 0$$$. In this case, we will draw an undirected edge between the points $$$x - d$$$ and $$$d$$$. Recalculate the dynamics for point $$$x$$$ as follows $$$dp[x][d] = max(dp[x][d], dp[x - d][d] - 1)$$$
Dynamics base, initially for all $$$x$$$ and $$$d$$$, $$$dp[x][d] = 0$$$. Now for all m triples $$$a_i, d_i, k_i$$$ we get $$$dp[a_i][d_i] = max(dp[a_i][d_i], k_i)$$$
At the end, using dfs, we will find the number of connectivity components
Code of this solution: 283668708
i did similar but used dsu for counting
In the editorial of F, I think it should be $$$f(p^{ik},d)$$$ instead of $$$f(p^{i}k,d)$$$
https://mirror.codeforces.com/contest/2020/submission/283572788
can anyone help me why above is wrong
might be a rounding issue. generally a good idea to avoid non-integer types unless absolutely necessary
Where's the originality?
Problem Codeforces 976 Div2 $$$F$$$ be directly copied from AtCoder Beginner Contest 370 G link: https://atcoder.jp/contests/abc370/editorial/10906
The core idea of both problems is absolutely identical, including the approach of solving them with a convolution technique. The only noticeable difference between the two problems lies in how the function $$$f(prime)$$$ and $$$f(prime^{ki}, b)$$$ is computed. Other than that, the rest of the structure, including the logic and solution techniques, are the same. This raises concerns about originality and fair practice in problem setting across competitive programming platforms.
Problem Codeforces 976 Div2 $$$E$$$ has solution with the most basic dp idea with $$$O(n \cdot 1024)$$$.
As someone who placed officially 12-th in Div 2, I’m absolutely disappointed with how Codeforces 976 Div2 F turned out.
..
An alternate solution to D which doesn't use DP:
Similar to the solution in the editorial I used a DSU to keep track of components, but to check whether elements $$$i$$$ and $$$i+d_i$$$ are connected, I simply need to check among operations $$$j$$$ where $$$d_j = d_i$$$, and $$$a_j \% d_j = i\%d_i$$$. I used a map to store sets of operations together based on $$$d_j$$$ and $$$a_j\%d_j$$$, and I stored each operation as a pair $$$[ a_j, a_j + k_j \cdot d_j ]$$$.
Now each set of operations can now simply be represented as sets of intervals, and I used a datastructure which I called an
IntervalSetwhich internally uses anstd::setto efficiently a insert intervals in amortized $$$O(\text{log n})$$$ and store them efficiently by combining overlapping intervals and query whether an interval is completely included in the set in $$$O(\text{log n})$$$ where $$$n$$$ is the number of intervals in the set. This allows me to simply query whether $$$[i,i+d_i]$$$ is included in the among the operations with $$$d_j = d_i$$$, and $$$a_j \% d_j = i\%d_i$$$ which makes the code very simple.My submission: 283669482
PS: I used ChatGPT to help in implementing the IntervalSet class so its not in a great state rn;) and I haven't seen any implementations of such an IntervalSet class, so I would love to learn about any other implementations you guys know about.
I think you can use a normal
setor even just avector, then sort the intervals within each $$$(d_i,a_i \bmod d_i)$$$. 283682972is that a percy jackson profile picture?
Yes it is!!
problem B solution without Binary search : solution
problem a can be solved by take log?
I also have the same question!
Yep it can be.
I try your solution but it got tle on testcase 3
Hey, did you get the answer? I have been racking my brain around this for a day:
Check my comment: Comment-1203949
hmm really?
check out this submission, my submission didn't get tle:
283695273
I saw your submission. I used #define endl '\n',endl flushes the output making it slower. and you should also use
ios_base::sync_with_stdio(false); cin.tie(nullptr);Hi, I've used
#define endl "\n"as well...Also used these in my main function, please check again :) Highly unlikely that these have anything to do with the WA though!
I was replying to thuctapsinh.
About you, I looked at your comment, both of the submission link you put are accepted so I don't really get what you meant.
Just want to point out: You are not actually using the log function to find out the highest power of k, instead you have used an iterator to find it out. So not really applicable to my doubt. I have found a similar solution which got AC but the entire point is that why is
log()not workingWhat do you meant by using iterator? I built my own ceiled log function for it.
The for loop inside the log function is what I'm referring to... Nevermind, thanks for the help!
Look at my profile submission, I have tried using your version of the code and it got accepted in GCC 14 and GCC 13 but rejected in GCC 7 that may be the issue.
How can one figure this out in a contest! :( Though I used C++20 as my compiler in the contest, still gave a WA on Testcase #4... Can you check out my WA code? The logic seems to be right, it still gives a WA
I found out my code got TLE because I miss "#define int long long" line, Thank you for the solution! It's very helpful!
thx a lot ,but why when i use log(n)/log(k) didnot work ,(log here is bultin function)
Checkout this submission of mine, here I used log(n)/log(k) 283840657
i found that you use GNU G++20 13.2(64bit ,winlibs) but i use GNU G++17 7 .3.0 so your code and my code got wrong answer on test2 if i use GNU G++17 7 .3.0 but it give me accepted if i use GNU G++20 13.2(64bit ,winlibs) . because GNU G++20 13.2(64bit ,winlibs) has more features and updates . thank you very much , i got a good information!
Yep to be more precise, programming languages are bad at floating points, log returns float/double, it may return 3.99999 which when converted to int becomes 3 and it will cause error. GNU G++ 20 and above solves this as it problem. To do it in GNU 17, you need to make your own log function as I did earlier or Search for articles (especially before 2020) in codeforces to deal with it.
Although I know $$$O(1204\cdot n)$$$ is not the standard solution to E, I have encountered a strange TLE in this solution by just moving $$$M = 10^9 + 7$$$ to the inside of the $$$solve()$$$. 283686661 283686119 Could anyone tell me what's going on?
if you put it outside pypy compiles it as constant, which is way faster.
Could someone please explain what is wrong here?
During the contest, I took limits of 1 to 1e18 (wrong, I later realised why), tried upsolving with 1 to LONGMAX, 1 to 2e18. all wrong. ~~~~~ void solve() { ll k; cin >> k;
ll low = k, high = 2e18, res = -1; while (low <= high) { ll mid = low + (high - low) / 2; ll sqcnt = floor(sqrt(mid)); ll ON = mid - sqcnt; if (ON == k) { res = mid; high = mid - 1; } else if (ON < k)low = mid + 1; else high = mid - 1; } cout << res << "\n";} ~~~~~ Sorry if the code is bad/unreadable. Thank you for your time.
Just in case, if link to submission is needed. https://mirror.codeforces.com/contest/2020/submission/283589596
Thank you!
Good Day ,
Please replace sqrt with `sqrtl' to avoid precision error.
Please help for question B :
why this submission: https://mirror.codeforces.com/contest/2020/submission/283695028
Gives wrong answer on test 6.
I tried locally with generated test cases my answer is exactly same as the editorial code. No diff.
Why this code is failing at test 8.
why binary search in editorial works perfectly, i mean both are doing the same things.
I have the same question as "gehadd." Can someone please help us out? tion. Someone please help..
boss take sqrtl and check again. if it works.
try sqrtl
yeah it worked, thank you
I have created a video solution for Problem B and Problem A on my youtube channel, please check it out, it's a simple and intuitive solution
Video solution for Problem C
For E I used the dumb O(1024*n) solution but idk why I'm TLEing. For this submission 283708821 it TLE test 12 since I did dp%MOD. But for the previous submission 283708742 it passes, but I all did was changing the MOD so that it MODs the whole thing instead of the dp itself. How in the world is this not the same thing???
Pls help if anyone know the issue thx <3
change to C++23, there will be probably some magic coming out...
damn do you know why this is?
Can someone plz explain the problem A solution why we use % and / and how it is related to powers (k^x)
take example of n=6492 and k=10 to make it 0 we will first apply 6 operation of 1000(10^3) 4 operations of 100(10^2) 9 operations of 10 (10^1) and 2 operations of 1 (10^0) thereby total operations are 6+4+9+2 =21 but here base is 10 now if we generalise this for kth base ans is sum of digits in kth base . This is because each non-zero digit corresponds to an operation that subtracts some multiple of a power of k now we can extract digits in base k similar to how we do in decimal base .but instead to 10 we mod by k
Thank you so much it really helps me to understand the problem.
F can also be solved using standard min_25 sieve trick: https://mirror.codeforces.com/contest/2020/submission/283749226
My O(N * D) solution for D
Can someone help me understand why: 283765681 gives WA But: 283765681 gives AC
In the AC solution I just decrease the number of while iterations by subtracting from n multiples of maximum allowable k^x.
Whereas in the WA solution, I decrease the maximum allowable k^x one at a time.
For problem C why is it giving WA on test-11?
283777193
Hello, did you find what the error is? I have a similar problem in WA 11.
I have changed the approach, after lot of WA!
j * (1 << i)is an integer, changing it toj * (1LL << i)should do!Oh yes! It worked.
Thanks :)
Thanks a lot, i had the same stupid mistake
Binary search for Problem-B gives WA on test-8. 283788662
Can someone pls explain E, how DP is being applied?
in problem d can't we just make a graph with the help of dsu with the help of given nodes that we receive during input and then calculate the number of connected components?
My solution:https://mirror.codeforces.com/contest/2020/submission/283746432
i did same, don't know i expected tle but i got WA can somebbody explain
if you guys get the answer can you please explain to me also?
before adding to the map... and make ds.parent[i] = ds.findupar(i);
In problem A, i do
till n is bigger than zero and count the operations Can anyone explain why it is wrong? It passes the provided test cases but fails on pretests
Looking at the tutorial of problem E, it isn't clear why the contribution of pairs of bits from both operands can be added together. When we think about the multiplication, we observe that multiple pairs $$$(i,j)$$$ can affect the same bit of the result and yield a carry over. Thus, we don't know a priori if that bit will be set (with some probability) or not, but the contribution should only count when the bit is set.
However, after some consideration, I've concluded that it doesn't matter whether the bit will be set. What matters is that the contribution of all pairs will add up (in terms of expected value), just as it would in the multiplication. Please correct me if I'm wrong in this reasoning.
f(S)^2 = \left(\sum_{i=0}^{B}{b_i \cdot 2^i}\right) \cdot \left(\sum_{j=0}^{B}{b_j \cdot 2^j}\right) \\
f(S)^2 = \sum_{k=0}^{2B}{\left(2^k \cdot \sum_{i+j=k}{b_ib_j}\right)} $$$
Yes, it doesn't really matter whether there is carry over. It's just convenient to look at the number in base 2, that's all.
I see it now, thx!
Can someone please clarify my doubt regarding the constraints in problem B.
In my Binary search approch 283836255. The code got accepted but looking at the constraints since k can be 1e18 then answer will be more than 1e18 right. but why are we using long long instead of unsigned long long here and truncating our values?
For problem A, can someone explain why solving the problem for n is equivalent to solving the problem for n/k in case k divides n.
I understand that if n is a multiplier of k, then we don't need the operation of subtracting 1.. and we solve by subtracting k, k^2, ...
But what proves that the min number of operations required to solve for n/k is equal to that required for n in such case?
bro $$$E$$$ is so easy so yet so less accepted submissions , I missed out too , easiest problem in the contest if you know how to do memory optimisation in DP
The same solution problem B in JAVA does not work
In problem E, I tried O(n * 1024) and got tle, so I spent a lot of time to optimize it and did not have enough time to solve D.
And after contest finish, I knew that just need to add ios::sync_with_stdio to get AC
Can someone tell me how I can solve B in java? As far as I know there's no equivalent of sqrtl() in java and Math.sqrt() introduces precision errors for larger inputs.
You can just use binary search to find square root.
Tip for anyone solving B:
go for the Binary Search solution Also to learn and think how to came to solution, just iterate through some cases. It took me while to figure out but once you do, it becomes easy
After testing multiple cases for problem C, I found that the correct answer is a=((b&c)⊕d), but I couldn't determine the exact reason behind this result. If anyone understands please help
why is this not a valid solution for C? 284331257
mmm, i thinking i better formula for B can be
ans = k + floor(sqrt(floor(sqrt(k))) + k))
the m = floor(sqrt(k)) is for know how many perfect squares be in the number k, and now we have the possible ans s. So the answer will be s = k+m;
But we have to verify if the gap between k ans k+m there is not another perfect square, so we have do the same process: ans = k + s + (s — (k+floor(sqrt(s))))
and with some algebra we can end with ans = k + floor(sqrt(s)) how the final answer, with s=k+floor(sqrt(k))
I tried my best for make the comment clear, sorry , i'm not good expressing ideas :(
why 0.5 was added in answer in B
Thanks for the editorial
in the editorial of problem D, can anyone please explain/elaborate the following:
What do we mean j is not a + k*d ? how can j node be a part of connection if it is not representable as a + k*d ?
The binary search in Question B is still a bit difficult to understand. For example, when k=6, both n=8 and n=9 can be calculated on a computer as diff=n-sqet(n)=6=k. So how can this issue be avoided?
you have to find the smallest n satisfying n-sqrt(n) = k so in the code also when mid-sqrt(mid) >= k then r = mid and else l = mid which ensures that l will be the largest number such that l — sqrt(l) < k and r will be the smallest such that r-sqrt(r) >= k.
the link to the book isn't working (B)
can someone explain why for A the following logic is giving WA