В этой задаче нужно было промоделировать то, что написано в условии. Также можно показать, что ответом является формула 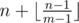 , где под ⌊ x⌋ понимается целая часть числа x.
, где под ⌊ x⌋ понимается целая часть числа x.
Заметим, что S(x) может принимать только целые значения и 1 ≤ S(x) ≤ 81. Переберем S(x) от 1 до 81, и посчитаем значение выражения B * S(x)A + C. Затем, если сумма цифр полученного числа совпадает с S(x), число положительное и оно меньше 109, то оно является решением. В этой задаче могли возникнуть проблемы из-за использования встроенной в C++ функции pow()
Заметим, что ответ положительное число, не превосходящее 109 + 105. Найдем ответ, используя бинарный поиск по ответу. Действительно, мы можем проверять за O(n) можно ли достичь определенной высоты. Для этого идем слева направо. Для текущего цветка посчитаем какое минимальное количество раз нужно полить текущий цветок, что бы он стал высоты не менее, чем проверяемая. Если текущий цветок нужно увеличить на h, то начнем h отрезков в этом цветке. Будем хранить массив, в котором st[i] — количество отрезков, начинающихся в i-ом цветке. Так же будем поддерживать переменную, в которой будем хранить количество отрезков, в которых содержится текущий цветков. Этот счетчик можно обновлять за O(1). Действительно, когда чтобы получить новое значение из предыдущего, достаточно отнять st[i - w], и, если мы создаем новые отрезки, прибавить st[i].
Также можно доказать, что работает простая жадность. На каждой из m итераций можно искать левейший цветок минимального роста, и поливать отрезок, начинающийся в этом цветке. Реализация "в лоб" отрабатывает за O(nm), поэтому для реализации нужно использовать структуру данных, поддерживающую операции взятия минимума и множественного прибавления на отрезке. Помочь в этом деле могут sqrt-декомпозиция или дерево отрезков с ленивым обновлением. Эти решения работают значительно дольше первого, но влазят в TL. Доказательство: Рассмотрим любую оптимальную последовательность ходов (то есть такую, при которой достигается максимальный ответ). Рассмотрим цветок, который изначально был самым левым из минимальных и рассмотрим все отрезки, в которых он содержится.(Предположим он содержится хотя б в одном отрезке, так как иначе, ответ равен начальной высоте этого цветка, а значит мы можем начать отрезок в этом цветке, и ответ не изменится). Предположим, нет отрезков, начинающихся в нем. Тогда рассмотрим отрезок, который начинается правее всех остальных (если их несколько, то любой такой). Тогда верно следующее: мы можем подвинуть этот отрезок вправо, так, чтобы он начинался в минимальном левом цветке. Действительно, цветы которые раньше находились на этом отрезке изначально были строго выше минимального и поливались как минимум столько же раз, сколько и минимальный. Значит после того, как мы сместили отрезок, их высота осталась не меньше, чем высота изначально минимального левого цветка. Таким образом новая последовательность ходов также будет оптимальной. Значит есть последовательность ходов, которая содержит отрезок, начинающийся в левом минимальном цветке. Тогда применим этот отрезок. Аналогично будем поступать в остальные дни, и тогда высота самого низкого цветка будет максиммально возможной.
Если r - l ≤ 4, то можно перебрать все варианты. Иначе, если k = 1, очевидно, что ответ l. Если k = 2, то ответ 1, т.к. можно выбрать числа 2x и 2x + 1, и их xor равен 1. Если k ≥ 4, то ответ 0, т.к. можно выбрать две пары чисел с xor 1, и их xor будет равен 0.
Осталось разобрать случай когда k = 3. Если k = 3, то выбрав числа 2x и 2x + 1 можно достичь значения 1. Поэтому остается узнать, можно ли получить xor равный 0. Предположим, существуют три числа x, y и z (x > y > z) которые лежат на отрезке [l, r], и их xor равен 0. Рассмотрим старший значащий бит числа x. В этом же разряде числа y тоже 1, т.к. xor равен 0, а y > z. Рассмотрим следующий бит. Если у z там стоит 0, то сделаем следующее: в предыдущем разряде чисел x и y 1 заменим на 0, а в этом бите чисел x и y поставим 1, если там был 0. Очевидно xor остался равным 0, число z не изменилось, а числа x и y стали ближе к числу z, поэтому они остались на отрезке [l, r]. Рассмотрим следующий бит чисел. Если там у z опять стоит только нуль, то опять заменим старшие биты в числах x и y и т.д. Т.к. z > 0, то когда-нибудь мы придем к разряду, в котором есть 1. Так как xor равен 0, то у числа x в этом разряде тоже 1 (x > y), а у числа y в этом разряде 0. В последующих разрядах будем заменять бит в числе x на 0, в числах y и z на 1. От этого число z будет не уменьшаться, а x не возрастать, при этом x > y > z будет оставаться верным. В итоге получили следующее: если такие три числа существуют, то существуют и три числа вида
1100…000
1011…111
0111…111
xor которых равен 0. Таких троек мало, поэтому их можно перебрать
Формальная постановка задачи: даны натуральные числа R — радиус окружности, и N. Требуется выбрать N не обязательно различных точек A1, A2, ...AN лежащих внутри или на границе окружности, таких, что величина
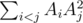
максимальна.
Сперва обозначим за 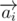 вектор, ведущий из точки начала координат в точку Ai. Величина
вектор, ведущий из точки начала координат в точку Ai. Величина 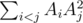 теперь равна
теперь равна 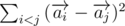 , что равно
, что равно 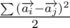 , а это нетрудно расписывается как
, а это нетрудно расписывается как 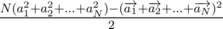 . Это наводит нас на мысль о том, что точки выгоднее расположить как можно ближе к окружности, чтобы |ai2| был как можно больше, но сделать это надо так, чтобы
. Это наводит нас на мысль о том, что точки выгоднее расположить как можно ближе к окружности, чтобы |ai2| был как можно больше, но сделать это надо так, чтобы 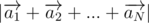 было как можно меньше. В частности, становится очевидным, что если N четно, то можно выбрать один из диаметров, и половину точек покидать в один конец диаметра, а половину — в другой. Теперь попробуем сформулировать все более строго. Пусть мы нашли расстановку точек, на которой наше выражение достигает своего максимума. Обозначим координаты точек как (x1, y1), (x2, y2), ..., (xn, yn). Пусть первые N - 1 точка фиксированы, а координаты последней мы можем двигать — обозначим их, как (x, y). В терминах этих координат, мы хотим максимизировать выражение
было как можно меньше. В частности, становится очевидным, что если N четно, то можно выбрать один из диаметров, и половину точек покидать в один конец диаметра, а половину — в другой. Теперь попробуем сформулировать все более строго. Пусть мы нашли расстановку точек, на которой наше выражение достигает своего максимума. Обозначим координаты точек как (x1, y1), (x2, y2), ..., (xn, yn). Пусть первые N - 1 точка фиксированы, а координаты последней мы можем двигать — обозначим их, как (x, y). В терминах этих координат, мы хотим максимизировать выражение
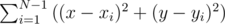
Все квадраты, где не участвуют x, y мы отбросили. Максимизация этого выражения раскрытием скобок и отбрасыванием констант сводится к максимизации
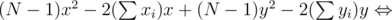
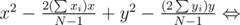
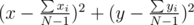
Таким образом, мы свели задачу к тому, чтобы найти наиболее удаленную целочисленную точку от точки с координатами
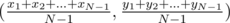 . Теперь мы сделаем очень важный вывод: наиболее удаленная целочисленная точка находится в одной из вершин выпуклой оболочки всех целочисленных точек, находящихся в круге. Доказательство. Обозначим имеющуюся точку за T, а наиболее удаленную от нее, находящуюся в выпуклом многоугольнике P за X(она, очевидно, содержится в выпуклой оболочке). Теперь продлим TX до пересечения с одной из сторон многоугольника — обозначим этот отрезок за AB, а точку пересечения за X'. Ясно, что TX' ≥ TX. Нетрудно видеть, что один из углов
. Теперь мы сделаем очень важный вывод: наиболее удаленная целочисленная точка находится в одной из вершин выпуклой оболочки всех целочисленных точек, находящихся в круге. Доказательство. Обозначим имеющуюся точку за T, а наиболее удаленную от нее, находящуюся в выпуклом многоугольнике P за X(она, очевидно, содержится в выпуклой оболочке). Теперь продлим TX до пересечения с одной из сторон многоугольника — обозначим этот отрезок за AB, а точку пересечения за X'. Ясно, что TX' ≥ TX. Нетрудно видеть, что один из углов 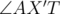 и
и 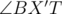 — тупой,следовательно, по свойству тупоугольных треугольников, или TA ≥ TX' ≥ TX или TB ≥ TX' ≥ TX, то есть, точку X можно заменить на одну из вершин оболочки и расстояние может лишь увеличиться.
— тупой,следовательно, по свойству тупоугольных треугольников, или TA ≥ TX' ≥ TX или TB ≥ TX' ≥ TX, то есть, точку X можно заменить на одну из вершин оболочки и расстояние может лишь увеличиться.
Таким образом, каждую точку оптимального набора мы можем считать лежащей в вершине выпуклой оболочки. Соответственно, решение — перебрать всевозможные наборы точек и посмотреть значение выражения для них. Если R ≤ 30, то на выпуклой оболочке содержится не более 36 точек — можно проверить с помощью компьютера. Таким образом, перебор всех наборов точек займет порядка 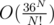 , что вполне укладывется в тайм-лимит, возможно, с некоторыми оптимизациями.
, что вполне укладывется в тайм-лимит, возможно, с некоторыми оптимизациями.
Немного о реализации перебора: в каком-то векторе хранится выпуклая оболочка. Заводится рекурсивная функция, параметры которой это:1) сколько точек уже добавлено 2) ссылка на вектор с точками 3) сумма x-координат точек 4) сумма квадратов x-координат точек 5) сумма y-координат точек 6) сумма квадратов y-координат точек.
На каждом этапе рекурсии берется последняя добавленная в растановку точку, и в расстановку по очереди добавляются точки, начиная с нее и до конца выпуклой оболочки — это начинает новый этап рекурсии. Также мы достаточно очевидно пересчитываем текущую мощность — это делается с помощью 3, 4, 5 и 6го параметров.
На самом последнем этапе, когда мы уже взяли N точек, мы определяем, была ли у нас когда-нибудь столь большая мощность. Если нет — копируем его во внешнюю переменную maxvalue, а набор точек — во внешний объект bestvector.
UPD Разбор задачи C был дополнен











В E заходит рандом, если случайным образом выбирать точки и обновлять ответ передвигая точки на более выгодные места. По-крайней мере трех секунд хватает, чтобы найти оптимальный ответ с нескольких запусков. Если бы не опечатка в индексе, то и на контесте зашло бы :( 7534644
Интересно. Хорошая идея. Я думал, не прокатит (у меня не прокатило:))
Limit is 10^9.. checking till digit sum 72 -_-
I'll not forget this round!
10^9 has 10 digits, which means that the highest reachable number can be 999999999; S(999999999)=81.
Same mistake!! Became Green as a result!! HOW!
same mistake TT
done same and got hacked
Wow, very fast editorial. Thanks for it!
TL по задаче Е меньше чем 2х(авторское решение на плюсах) это, конечно, круто.
Мне вот интересно, а авторы сами умеют упихивать на джаве решение в такой TL? Имеется ввиду без предподсчета и на нормальных тестах. Кстати, сейчас все сданные на джаве решения (а также некоторые на плюсах) упадут на тесте "3 28" :)
Изначально предполагались более жесткие ограничения — количество точек до 8, радиус до 50. Использовались некоторые оптимизации перебора и умение решать задачу за O(1), когда n четно. Потом мы пришли к выводу, что следует сделать задачу более решабельной без использования математических рассуждений (т.е. чтобы мог зайти хитрый рандом или простой перебор) и ослабили ограничения. 2x действительно упало до (3/1.653 = 1.8)х, но учитывайте, что достаточно очевидное наблюдение о четном n снижает время работы до 400мс. Таким образом, ваше заявление о том, что мы подгоняем тайм-лимит под авторское решение кажется несколько безосновательным.
Я говорю о том, что хорошим тоном считается ставить TL в два раза больше времени авторского решения на джаве.
А сейчас получается, что аккуратная реализация того, что описано в разборе, работает где-то 4,5с (хотя, возможно, я не умею писать аккуратно?).
P. S. а сама задача довольно интересная :)
coded the same algo as written in Problem B
but was unaware of the issue with C++ pow() and hence became newbie :/
You learn from your mistakes. Be glad that it's only an online competition. I lost a national olympiad silver medal because pow(10,2) gave me 99, but I knew what to do now. :)
Какие-какие отрезки жадно создавать справа налево?
Я сам не понял. Я решал что-то вроде динамикой. Создал два массива
b[]иc[]. Вbхранилось сколько раз я полилiцветок, а вc— сколько раз полилiцветок, при этом этот цветок является первым в поливе. Поэтому формула имеет следующий вид:b[i] = b[i - 1] - c[i - w]. То есть данный цветок мы полили столько раз, сколько полили и предыдущий, за исключением тех случаев, когда мы начинали поливать цветок находящийся на расстоянииwот данного. То есть полив цветка на расстоянииi - wвлияет на полив цветкаi - 1, но не влияет наi.То есть вы каждый раз выбираете наименьший цветок, например на позиции i и поливаете интервал [i, i + w), меняя с[i]?
Это слишком долго. Я просто один раз иду по всем цветам, если текущий цветок необходимо полить:
a[i] + b[i] < x(b[i] = b[i - 1] - c[i - w],x— минимальная высота цветка, которую я проверяю), то поливаю его ровно столько, сколько необходимо, чтобы он стал высотойx, то естьc[i] = x - a[i] - b[i], и прибавляю это количеству к результату — количеству дней, которое необходимо, чтобы все цветы стали высотой не меньшеx, и если это значение стало больше, чемm, то такой высоты мы не можем достигнуть.Если что, я имею ввиду, что так выглядит функция
check()при решении бинарным поиском. То есть время работы алгоритмаO(n * log2( 10^9 + m ) ).can someone please explain what does the check() function actually check for/how it works, in the referred submission of Problem C
http://mirror.codeforces.com/contest/460/submission/7536171
I also couldn't understand the check() function,do you make it??
yeah I got most of it.. see the updated editorial for problem C
I'm curious about the greedy solution for C. When we find the leftmost smallest element (let's name it L), do we always water flowers [L, L+W] (except when you can't go right anymore)?
Suppose you're going from left to right, and the current position is i. This means that all flowers before i have already been watered enough. Now if the flower at position i is too short, then we conclude that we need to water it x times, and that there is no point in watering the flowers to the left -- it does not improve the answer. So the only choice left is to water the [i, i + w) segment x times.
Could you help me debug this submission 7543565? It seems that I have an infinite loop in my binary search (test case 20), but I can't seem to find it.
The complexity is O(nw), so I doubt the approach is wrong (although I admit it could be optimised).
O(nw) (with a hidden constant factor due to the binary search) is too slow for this problem, because the statement says 1 ≤ w ≤ n ≤ 105.
You need a faster way to do range updates. Some people used a segment tree for this, and some other maintained the current added height and an array of where and how many watered segments end.
Yes. Think like this. You start with the first from the left: if its high is more or equal to the solution you're trying, then there is no problem and you continue to the next one; if high is less than the solution, then you have to water that flower (solution-high)times and, of course, you water also the flowers to the right (because the ones to the left are already ok).
Hope this helps :)
C++ pow() functions bug ? Could someone explain this for me please ?
The default pow() from the C++ STL (the one in <math.h>) returns a double, not an integer.
By using a double you are prone to rounding errors (if you are not aware why, research on how are doubles stored), which can sometimes offset a whole number when casting to integer (2.9999999999 can be cast to 2), which can give you a wrong result.
These rounding errors might seem rare, but in ~100 test case at least one is sure to produce it. This is why you should use your own pow function instead, something like :
This will return an integer, making sure you don't get a rounding error.
I think it is if( b== 0) return 1;
Should have been a 1 there, fixed it now.
can anyone explain 460C?? I am unable to get the question?? for the first test case 2 2 2 1 1 1 after 1st day 2 2 2 3 2 2 why din he water for 2nd day so that it would result in 2 2 2 4 3 3 so that 3 is the maximum height of the smallest flower i.e., 1 at the beginning
2 2 2 4 3 3 the maximum height of the smallest flower is 2. it does not mean the height of the smallest flower in the 1st day, but in the m-th day.
В разборе не написаны частные случаи, когда k = 2, то ответ всё равно l. Например: 1023 1024 2.
Точно!
Great contest!
Till now I could not believe that my simple back — tracking solution passed E (shocked when looking at the editorial).
The main idea of our solution is to prove, that optimal rearragement of points lies on the convex hull and brute-force it. Could you explain your solution?
In the contest, when I saw n <= 8, I think that may be brute-force works. I tried to implement a slow brute-force consider all points in the circle and realize that there is a 'pattern': if n is even, then we only need points of types (0; r) and (0; -r), else with odd n, it is sufficient to use the points which have maximum distance from O (there are 8 points which have that property), plus 2 points (0; r), (0; -r), we get 10 points in total. So a back-tracking algorithm to deal with these 10 points is enough ! (Actually in my solution, I use up to 27 points, just to ensure the correctness). It seems that the solution described in the editorial uses the same idea as mine, but it need to check all points on the convex hull. Anyway, these are only guesses, I cannot prove it yet.
In the problem c, Can anyone please explain the 2nd technique to solve the problme?
I solved the problem using Sqrt-Decomposition.
What you basically do is that, break the array into sqrt(n) groups of about sqrt(n) elements. Read Here( I read it after translating to English via Google Translate ) Then for each group, you store the minimum element in an array(of size sqrt(n)), with its index.[ Complexity: O(n) ]
Repeat this process m times-> - Find the minimum element in the new array(of size sqrt(n)).[ Complexity: O(sqrt(n)) ] - Then for the minimum element in the whole array, you update the indexes from i (of the min element) to min(i+w-1,n-1) by +1. The process of updation is explained quite well in the article above.
After this process, find the minimum element in the sqrt(n) sized array, and thats your answer.
Overall Complexity: O(m*sqrt(n)) 7558102
I'm new to this concept, but I liked it a lot. All those familiar with Sqrt-decomposition, pls give me some tips as to when and where to apply this concept.
isn't sqrt decomposition just like a worse version of segment tree..
There is no need to use data structure. Look at this. 7521845 (Sorry,I chose Russian by mistake..)
There could be other solution, which use data structure, but doesn't use binary search
Oh sorry. I misunderstood the editorial.
In Problem C, what exactly is "sqrt-decomposition" method?
link
Can anybody explain why the segment tree approach would be correct? I got the idea during the contest but I wasn't sure whether the idea is correct. How can we justify that approach?
what is sqrt-decomposition? I have searched it but founf nothing? could someone tell me? in Chinese if can? thx
In English
Thx!
fast tutorial. great!
Can someone please help me? According to codeforces my solution for Prob 2 fails pretest 8 but on my PC as well as ideone, it works and gives the required output!! here is my solution solution in ideone
You forgot to initialize the variable
suminsum(). And you assign the result of the formula computation tolong int, but it may requirelong long.In addition to andreyv' remarks: You don't check that your answers are in the allowed range. From the problem statement: "Print only integer solutions that are larger than zero and strictly less than 10 ^ 9."
del
Hi, I solved 460A correctly but i would like to understand the more elegant and mathematical solution posted by this editorial. Can anyone explain why n + [(n-1)/m-1] is the formula ?
We can use mathematical induction on this. Suppose that by having n pairs of socks, Vasya receives a pairs of new socks and lasts for b more days since his last gift; thus Vasya lasts for am + b days.
Now, if we increment n by 1, we can ignore this extra pair of socks and let Vasya to get a pairs of socks and survive for b more days. Now we introduce our new pair of socks. If b ≠ m - 1, then our new pair of socks don't give Vasya any extra pair of socks; just one more day of surviving. On the other hand, if b = m - 1, then after using these socks, Vasya will get another pair, so this increments a and sets b = 1.
Now observe that b goes 1, 2, 3, ..., m - 1, 1, 2, 3, ..., m - 1, 1, 2, 3, ... in a cycle, so we can be sure that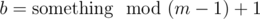 , since it is a repeating sequence of increasing integers of period m - 1, and it begins with 1. By a little trial and error, we get
, since it is a repeating sequence of increasing integers of period m - 1, and it begins with 1. By a little trial and error, we get 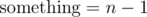 , so
, so 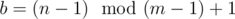 .
.
What about a? It begins at 0, and increases when n = m, 2m - 1, 3m - 2, ...; exactly when b = 1 (except for the first time where n = 1). Thus we need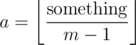 , so that we have a jump every m - 1 steps. Turns out that
, so that we have a jump every m - 1 steps. Turns out that 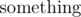 is n - 1, since we need
is n - 1, since we need 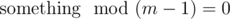 in order for the floor to increase.
in order for the floor to increase.
Now we have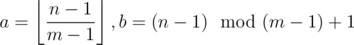 , we plug these into our formula:
, we plug these into our formula: 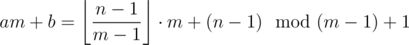 . Ouch, this will be messy.
. Ouch, this will be messy.
Let's split m = (m - 1) + 1. Then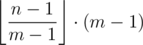 is simply the largest multiple of m - 1 not exceeding n - 1, and
is simply the largest multiple of m - 1 not exceeding n - 1, and 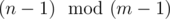 will add for the remainder, so we have
will add for the remainder, so we have 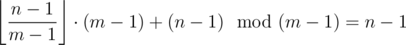 , exactly. Hey, this isn't bad! Adding the + 1 remaining, we get n, the first term of the sequence.
, exactly. Hey, this isn't bad! Adding the + 1 remaining, we get n, the first term of the sequence.
We are left with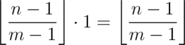 , which is just the second term of what we want to prove. So Vasya survives for exactly
, which is just the second term of what we want to prove. So Vasya survives for exactly 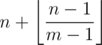 days with his socks, and he really needs to start doing laundry with his possibly 199 pairs of used socks present.
days with his socks, and he really needs to start doing laundry with his possibly 199 pairs of used socks present.
One can also solve E without any insights whatsoever ;)
By rewriting the formula you get that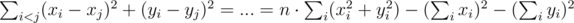 . Notice that we were able to get rid of all double sums. This gives rise to the following dynamic programming solution:
. Notice that we were able to get rid of all double sums. This gives rise to the following dynamic programming solution: 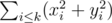 that you can get if you select k points such that
that you can get if you select k points such that 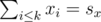 and
and 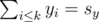 . The complexity is
. The complexity is 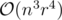 . This is too slow to pass, but you can precompute all the answers locally.
. This is too slow to pass, but you can precompute all the answers locally.
dp[k][sx][sy]is the maximum value of the sumYou can probably also prove that only border points are worth looking at. In this case, one step becomes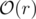 rather than
rather than 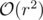 and you don't need precomputations.
and you don't need precomputations.
Anyway, this proves that there is a solution polynomial in n and r, rather than exponential as in the editorial.
You can take a look at my solution: 7529095.
How do you prove that only border points are worth looking at ?
I think they prove it above (in the editorial).
Consider a point that can be moved left or right: (x, y), added as the last one. Its addition incurs an increase in the answer of
while for addition of points (x + 1, y) and (x - 1, y), the increases are
If neither of these points gives a better answer, then V + , V - ≤ V, so
but combining these inequalities together yields 2(n - 1) ≤ 0, which is only possible for n = 1 (which we knew already — if there's just 1 point, it doesn't matter where we put it). Proof by contradiction complete.
I don't know what happens, but for problem E ,The solution run in my machine for about 8 sec. But in codeforces it's 373ms . Is codeforces that fast ? I am using intel core-i-5 with 4 GB ram. Here is my submission 7552805 . You can check it. and the authors solution takes 9 sec. So , CF is 9 times faster than my PC.
Did you compile without -O2 locally?
Problem C: Can anyone explain in more details how to find in O(n) if a fixed height is reachable? I didn't really get it. Thank you!
Iterate the input array from left to right. if you visit a flower with the height less than your fixed height, begin some watering from there, and continue. Now when you check the height of flower, consider your watering before (I call that Y), and add Y to current flower's height.
Because of each watering ends at some position, just subtract the amount of watering that start at position i-w from Y. So it's better to store st[j] which means the amount of watering you start at jth position.
I tried hard, but could not get how this while loop works to find 3 numbers whose XOR is 0, in sample solution for Problem D
Could someone please explain??
Link here: 7536186
See here. Basically you're generating numbers in the form 2·2i - 1, 3·2i - 1, 3·2i, which can be shown to have XOR of 0.
Hi can anybody explain why the segment tree approach would be correct in problem C? I cannot understand why that is the solution?
I have a question about 460E — Roland and Rose My deduction of the formula(and oops I think its right) ∑(ai−aj)/2 = N(a12+a22+....+aN2)−(a1+a2+a3+....+aN)2 (i != j) Does it have some problem?
Maybe you meant ∑(ai − aj) ^ 2 / 2 (i != j)?
In this case you can add to the left part ∑(ai − aj) ^ 2 / 2 = 0 (i == j), because (ai — ai) ^ 2 / 2 = 0.
why the value of |a1+a2+a3...+an| make no difference of the value of(a1^2+....an^2) in problem E?It difficult for me to prove it
Anyone mind proving how n+(n-1)/(m-1) (int n,m) is the correct answer?
Some one please check 11514761 it gives the right answer on ideone but wrong on codeforces?
pow function..got it!
Editorial was probably translated using Google Translator. All we have to do in problem D , Case K = 3 is maintain 3 Numbers Low , Mid , High initially {1,2,3} . Then at any point multiply all by 2 and add 1 to the lowest number(We want lowest number to increase faster and highest number to increase slower and maintain xor 0 so Mid's bit = 1)
hi there,can anyone please explain the editorial of div2 C using binary search approach?? i can't understand the following lines of the editorial :- "If cuurent flower need to be watered for h times, we will star h segments in current flower. We would keep array, in which st[i] — number of segments, which starts in i-th flower. Also, we will keep variable, in which we will keep number of segments, which cover current flower. This variable could be updated at O(1). Really, to get new value we just need to subtract st[i - w], and, if we create new segments, to add st[i]."
hi there,can anyone please explain the editorial of div2 C using binary search approach?? i can't understand the following lines of the editorial :- "If cuurent flower need to be watered for h times, we will star h segments in current flower. We would keep array, in which st[i] — number of segments, which starts in i-th flower. Also, we will keep variable, in which we will keep number of segments, which cover current flower. This variable could be updated at O(1). Really, to get new value we just need to subtract st[i - w], and, if we create new segments, to add st[i]."
You binary search for the maximum height possible for the lowest flower. And you validate the 'mid' of your binary search greedily. This is how you do it. Suppose you are at position i of the array. You already know how many times you have watered the w-length segments starting at each of 1,2,3..i-1 (you have stored these somewhere, i.e. ops[] in my code linked below). Then some of these already-watered segments will affect index i too, more specifically the segments which start at i-w+1, i-w+2,..i-1. Sum up the number of operations on these segments (let it be S). If current_height_of_i + S >= mid, then you don't need to do anything and you can move on to i+1. Else, you need to fill the deficit by watering the w-segment starting at i.
You can look at my code for reference. Hope that helps! :)
thank u... :3
For Vasya and Socks, a simple solution and code.
https://medium.com/@deeptechtalker/vasya-and-socks-codeforces-solution-460a-with-explanation-b4a5aa56c24b
can you explain why we took mod? I mean i get the problem that we were having where the last sock wasn't getting counted(like in 10,2 example). But why mod for that? Bear with me i'm a newbie :)
mod returns the remainder of the integer division, the of the link is based in a integer division n/m, however n is not necessary divisible by m, so the remainder of the disivion is unitized in the iteration, and if its value is unitized we should pass this value to the nexts iterations, because it can contribute to the other iterations.
Something like having the case 5 3, in the first iteration we have $$$5/3 = 1$$$, but with the remainder, in the next iteration n=3=1+2(the mod), so we can divide n again per m in the second iteration, having the answer 7, if we dont use the remainder the code will have just 1 iteration instead of 2.
Thank you for the editorial. The explanation for problem B is obvious.