Hello fellow Codeforcers ! I participated in Codeforces Round 977 (Div. 2, based on COMPFEST 16 - Final Round) last Saturday and I had a great time. I was composed and was able to solve A, B and C1 in just under an hour. I thought I was close to solve C2 as well, but it took me some more time after the contest.
Here is my thoughts and solution about the first 5 problems of the contest. Welcome to my humble green editorial !
2021A - Meaning Mean
My first thought was that choosing two elements of different parity would result in "loosing" a unit because of the floor operation. I then tried with toy inputs like $$$8,5,2$$$.
- $$$\lfloor \frac{\textbf{8}+\textbf{5}}{2} \rfloor = 6$$$, $$$\lfloor \frac{6+\textbf{2}}{2} \rfloor=4$$$
- $$$\lfloor \frac{\textbf{8}+\textbf{2}}{2} \rfloor = 6$$$, $$$\lfloor \frac{5+\textbf{5}}{2} \rfloor=5$$$
- $$$\lfloor \frac{\textbf{2}+\textbf{5}}{2} \rfloor = 3$$$, $$$\lfloor \frac{3+\textbf{8}}{2} \rfloor=5$$$
I could conjecture two propositions. First, an order of summation could yield an optimal solution even if it combined odd and even number together (like in the third option). Then, it seems important to combine the largest values in the last steps.
Suppose we consider the values in the same order as they are in $$$a$$$, and insert new values at the front. The result for 3 values is :
Without floor this rewrites as
First chosen values will appear in more operations, and consecutive division by 2 will reduce their impact on the solution. Operations with floor will only increase this effect by eventually penalizing the result by one unit.
My idea was to maintain a sorted array by combining the two smallest values and reinsert the result at the front.
Complexity
Initial sort of the array, and performing $$$n-1$$$ operation results in $$$\mathcal{O}(nlog(n) + n) = \mathcal{O}(nlog(n))$$$ complexity
What I've learnt
In first problems of a contest, identifying an intuitive strategy by looking at some key examples is often a good idea
2021B - Maximize Mex
A standard MEX problem. It felt easier than problem A. The general idea here is to iterate over $$$mex$$$ from $$$0$$$ to $$$n$$$ and test whether it is possible to obtain this value. It is possible iff :
- $$$mex \in a$$$, or
- $$$\exists 1 \leq i \leq n$$$ such that $$$a[i] \leq mex$$$ and $$$a[i]-mex \equiv 0 [x]$$$, i.e. $$$mex$$$ can be obtained from $$$a[i]$$$ by performing the operation of adding $$$x$$$ several times.
My approach during the contest was to sort $$$a$$$ and iterate over its elements. While the current element was lower or equal to the current $$$mex$$$, I'd store it as an available lower value w.r.t. its rest in the division by $$$x$$$ in a vector $$$over$$$. Then, I'd look for the number of stored values at the index $$$mex \% x$$$. If it is more that $$$1$$$, I can decrease it by $$$1$$$ and increase $$$mex$$$ by $$$1$$$. Else the real value of $$$mex$$$ has bee found.
The official editorial uses a more elegant solution. Values in $$$a$$$ can be sorted and counted in place inside of an array $$$freq$$$ of size $$$n$$$ in $$$\mathcal{O}(n)$$$. The algorithm then writes as follows :
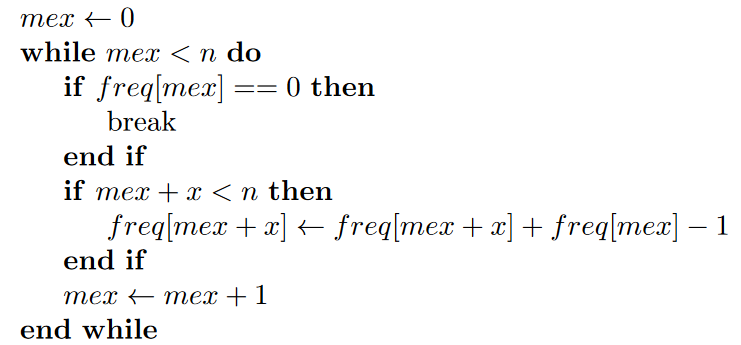
Complexity
Initial sort of the array, and iterating over values of $$$mex$$$ and elements of $$$a$$$ results in $$$\mathcal{O}(nlog(n) + m + n) = \mathcal{O}(nlog(n))$$$ complexity.
Official editorial reaches a $$$\mathcal{O}(n)$$$ complexity.
What I've learnt
I have solved several MEX problems, and I learnt that finding it's value is generally doable in $$$\mathcal{O}(n)$$$. I liked the idea of propagating overflow while looking for it.
2021C1 - Adjust The Presentation (Easy Version)
I tried to think of the first steps to check if a slideshow $$$b$$$ was good.
In the first step, we must have $$$b_1 == a_1$$$, since we couldn't make any decision on $$$a$$$
In the second step, we can have replaced $$$a_1$$$ at the front and have $$$b_2 == a_1$$$, or placed it somewhere else and have $$$b_2 == a_2$$$. Previously visited $$$a_1$$$ is considered to be in an available set of values for $$$b$$$.
In the third step, complexity arises :
- If we had $$$b_2 == a_1$$$, it means that we had to replace it at the front before the second step. The only available values for $$$b_2$$$ are either $$$a_1$$$ or $$$a_2$$$, the next available one.
- Else, we could have replaced $$$a_2$$$ at the front or somewhere else and could have a valid slideshow with $$$b_3 == a_1$$$ or $$$b_3 == a_2$$$ or $$$b_3 == a_3$$$.
- If we had $$$b_2 == a_1$$$, it means that we had to replace it at the front before the second step. The only available values for $$$b_2$$$ are either $$$a_1$$$ or $$$a_2$$$, the next available one.
My observation was that at each step $$$1 \leq j \leq m$$$, the prefix of the slideshow was valid if :
$$$b[j]$$$ was among the $$$k$$$ distinct previous visited values of $$$a$$$, or
$$$b[j] == a[k+1]$$$, and $$$b[k]$$$ would be a new visited value.
I used a unordered set to keep track of the visited values, and iterated over the elements in $$$b$$$.
Complexity
Iterating over values in $$$b$$$ results in $$$\mathcal{O}(m)$$$ complexity overall.
What I've learnt
This felt like the simplest of all three problems. However, I didn't solve it considering C2, and I didn't know at the time whether the approach was suitable to tackle the second part of the problem. In future contests, I guess that I should try to anticipate the next parts when looking for a solution.
2021C2 - Adjust The Presentation (Hard Version)
It's always challenging for me to start second part of a problem. In a problem with queries like this one, there usually are two parts to identify :
the deep structure of the problem, emphasized in part one, that has to be computed at least once,
the shared structure of the problem, that allows to handle queries sequentially without having to perform costly computation (often leveraging pre-computation).
My first naive solution handled each query independently : update of $$$b$$$ in $$$\mathcal{O}(1)$$$ and complete check in $$$\mathcal{O}(m)$$$. Of course, TL.
I couldn't find a way to reuse the unordered set from one query to another, so I had to find another structure that could be maintained. I identified that for a slideshow $$$b$$$ to be valid, I needed two conditions:
$$$b[1] == a[1]$$$
$$$\forall 1 \leq i \leq n-1$$$, $$$first[a[i]] \leq first[a[i+1]]$$$, where $$$first[v]$$$ holds the index of the first occurrence of $$$v$$$ in $$$b$$$, and $$$m+1$$$ if it's not in $$$b$$$
I defined $$$nbConflicts$$$ the number of conflicts in $$$a$$$, i.e the number of $$$i$$$ s.t. $$$first[a[i]] > first[a[i+1]]$$$. I used $$$ra$$$ the inverse permutation of $$$a$$$ ($$$ra[a[i]] = i$$$). To avoid the $$$\mathcal{O}(m)$$$ conflict check complexity, one should see that queries only create of solve conflicts locally, and this can be checked in $$$\mathcal{O}(1)$$$.
Before updating $$$b$$$, I decrease $$$nbConflicts$$$ for possible conflicts before and after the value $$$t$$$ in $$$a$$$, and before and after the value $$$b[s]$$$ in $$$a$$$. The four inequalities to check (if they exist) are :
$$$(first[a[ra[t]-1]] > first[t]])$$$,
($$$first[t] > first[a[ra[t]+1]]$$$),
$$$(first[a[ra[b[s]]-1]] > first[b[s]]])$$$,
($$$first[b[s]] > first[a[ra[b[s]]+1]]$$$).
I then updated $$$first[u]$$$ if needed. BUT. I couldn't find a way to update $$$first[b[s]]$$$ and kept doing i in $$$\mathcal{O}(m)$$$ and kept getting TL ...
I then realized I had freewill and could scroll comments under the contest blog, and I saw a comment by DuongForeverAlone with his submission 284562164. His solution was to maintain for each value $$$a[i]$$$ an ordered set of positions of $$$a[i]$$$ in $$$b$$$. This vector is computed only once at the beginning, and maintained in $$$\mathcal{O}(1)$$$ for each query, and we have first[b[s]] = *pos[b[s]].begin().
Complexity
Pre-computation of $$$ra$$$, $$$first$$$, $$$nbConflicts$$$ and $$$pos$$$ are done in $$$\mathcal{O}(n + mlog(m))$$$. Then for each query, the complexity of all operation is $$$\mathcal{O}(1)$$$, except the insertion of $$$s$$$ in $$$pos[t]$$$ in $$$\mathcal{O}(log(m))$$$. The total complexity is $$$\mathcal{O}(n + mlog(m) + qlog(m))$$$.
What I've learnt
- There is a specific mindset needed to tackled problems in several parts. I should try to anticipate the second part when solving the first
- In a query problem, it is always about precomputation and smart updates. Identify source of complexity in the query loop, and find how to reduce it this way.
- I genuinely didn't think of using std::set to maintain an ordered sequence (with an insertion cost of $$$\mathcal{O}(log(n))$$$). I'll keep this in my toolbox now.
- Finally, it took me some times to get this straight, and being able to do so in the time of a contest will be challenging for me !
2021D - Boss, Thirsty
This problem was really challenging for me. I understood that the possible scores for day $$$i$$$ were determined by day $$$i-1$$$, and I should probably build a dynamic array and update it day by day. The first challenge is to find a suitable representation of the solution at day $$$i$$$ that can be updated efficiently to produce a solution at day $$$i+1$$$.
If first thought of $$$dp[i][(a,b)]$$$, the best possible score that can be obtained on day $$$i$$$ by choosing range of products $$$(a,b)$$$. It would be the sum of :
the direct score $$$\sum_{c=a}^{c=b}(A_{i,c})$$$,
the best possible score of a compatible segment on day $$$i-1$$$.
Those segments $$$(a', b')$$$ must be such that $$$(a',b') \cap (a,b) \neq \emptyset$$$ and $$$(a,b) \setminus (a',b') \neq \emptyset$$$, which can be translated to :
$$$a \leq a' \leq b$$$, or
$$$b \leq b' \leq b$$$,
AND the extra condition that $$$(a,b) \neq (a',b')$$$.
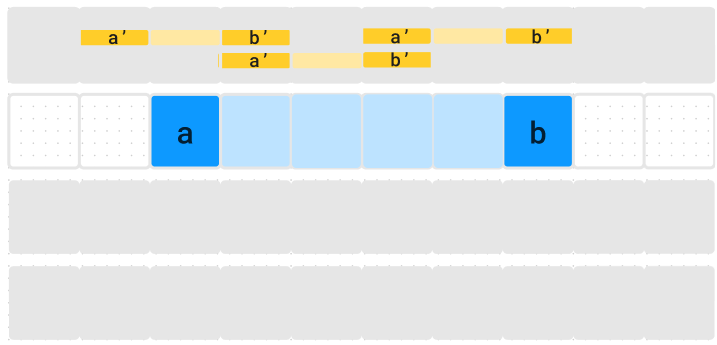
With $$$\frac{m(m-1)}{2}$$$ segments $$$(a,b)$$$ each day, the resulting complexity would be $$$\mathcal{O}(n*m^2)$$$. I thought of introducing $$$dpA[i][a]$$$ (resp. $$$dpB[i][b]$$$) the best possible score at day $$$i$$$ starting in $$$a$$$ (resp. ending in $$$b$$$). However, when trying to connect it with the previous day, I couldn't find a way to enumerate valid $$$(a', b')$$$.
Luckily, the official editorial came out and I started reading their solution. Their idea was to use $$$l$$$ and $$$r$$$ to describe the external edges of a segment rather than its end points.
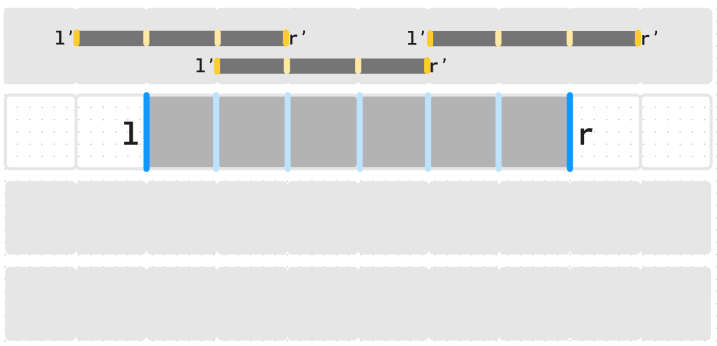
The conditions on previous segments $$$(l', r')$$$ then writes :
- $$$l < l' < r$$$, or
- $$$l < r' < r$$$,
without any further condition. This could be understood as "any compatible previous segment has an extremity strictly inside of the current segment".
We now introduce $$$dpL[i][l]$$$ (resp. $$$dpR[i][r]$$$) the best possible score obtainable on day $$$i$$$ using segment starting in $$$l$$$ (resp. ending in $$$r$$$). With $$$0 \leq \textbf{l} < \textbf{r}-1 \leq m$$$, we get
This looks much nicer ! For the next steps, I'll focus on $$$dpR$$$. For a given $$$r$$$, the exterior $$$\max$$$ can be computed in $$$\mathcal{O}(r)$$$ and the interior $$$\max$$$ in $$$\mathcal{O}(r)$$$. The resulting complexity of the algorithm would then be $$$\mathcal{O(n*m^2)}$$$.
Since we will compute values of $$$dpR$$$ for iterative values of $$$r$$$, we should try to share efforts and avoid recalculation.
The sum over $$$A_{i,p}$$$ can be expressed with prefix sums. Let's denote it $$$prefS[p] = \sum_{q=1}^{q=p}A_i,q$$$. It can be computed in $$$\mathcal{O}(m)$$$ for all $$$0 \leq p \leq m$$$, then
We now have
The next step requires to work with index bounds. I needed a long time to understand than $$$\max$$$ expressions can be commuted following this transformation
The left most expression can be illustrated with this picture. It is the max over columns $$$l$$$ of the max over all rows $$$p$$$ such that $$$l<p$$$.
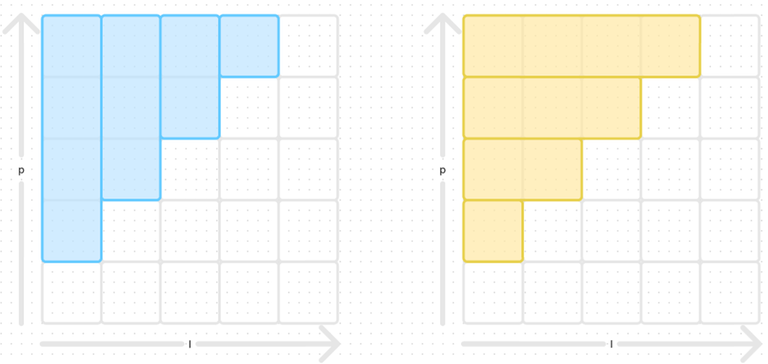
The right most expression is the max of all rows $$$p$$$ of the max over all columns $$$l$$$ such that $$$l<p$$$.
[pic]
Both describe the same area, and both of their values is the maximum of $$$f(l) + g(p)$$$ in this area.
The expression of $$$dpR$$$ can be written as
The rest is a gymnastic of prefix sums and prefix maximums.
$$$prefM[l] = \max{(prefM[l-1], -prefS[l-1])}$$$
$$$prefN[p] = \max{(prefN[p-1], prefM[p] + \max{(dpL[i-1][p], dpR[i-1][p])})}$$$
$$$dpR[i][r] = prefS[r]+ prefN[r-1]$$$
For $$$dpL$$$, remarking that the problem is symmetric allows us to simply reverse $$$A_i$$$ and use the same approach.
I had some trouble finding the right index ranges, recurring expressions, range end values of these structures and there may be still some mistakes here, but I got AC !
Complexity
Thanks to all prefix sums and maximums, the complexity is linear for each day and results in a $$$\mathcal{O}(nm)$$$ complexity.
What I've learnt
It was a very interesting problem, I loved it.
I had a really hard time working with indices, and I really doubt I'd able to do this during a contest. This is something I need to work on.
Prefix sum and prefix max allow to design really efficient approaches. Furthermore, they can be combined to build prefix of prefix and yield very elegant solutions.
Maybe I should take more time to look at other's submission to learn alternative approaches. I came along this super short answer by ecnerwala that I'm still trying to understand.
Thank you for taking some time to read this, I really appreciated doing it and will eventually continue for some recent contests. Let me know if I was unclear, or if you have suggestions to share on some problems.
Thank you ArvinCiu, CyberSleeper, athin and joelgun14 for writing this contest, and MikeMirzayanov for the amazing Codeforces and Polygon platform ! See ya










As the author of B, my initial solution was also $$$O(n\text{log}n)$$$ and someone else came up with the final $$$O(n)$$$ solution
This is the beauty of CP : generally there isn't a unique best solution, and nothing prevents future coders to find more effective algorithms.
This only occurs in nice problems though, so well done.