The following formula: F(n) = F(n-2) + F(n-1) + 1 give to me how many calls I need to generate the N-th term of Fibonacci. But I don't know how to handle the constant value + 1 to find the recurrence matrix.
I'm bit lost, and I found the following (but wrong) recurrence:
F(0) = 1, F(1) = 1
[F(0), F(1)] * [[0,2], [1, 1]]^(n-1) = [F(n), F(n+1)]
Can someone help me to understand ? Thank you.











In this case, you need a 3x3 matrix that converts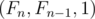 to
to 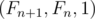 .
.
Alternatively, you could define Gn = Fn + c such that Gn = Gn - 1 + Gn - 2, find the constant c, calculate Gn and from it Fn.
Ok, I understand now, I'll try two ways that you gave to me.
I definitely solved this problem some time ago, cant remember when and where. Can you please provide the link?
Anyway, let G0 = 1; G1 = 1; Gn = Gn - 2 + Gn - 1 + 1. One can be proved that Gn = Fn - 1 + Ln - 1, where Fn - 1 is (n - 1)-th Fibonacci number and Ln is n-th Lucas number
https://www.urionlinejudge.com.br/judge/pt/problems/view/1033
The only thing to observe is that we can reuse the equation A(n-2) = A(n-2) to make a square matrix that are required for binary exponentiation. so,
A(n) = A(n-1) + A(n-2) + 1A(n-1) = A(n-1)1 = 1,using these three equations we can form the following matrixW = [[1,1,1], [1,0,0], [0,0,1]]now
M(n) = W * M(n-1)which is now a simpler version of the problem, here is a quick python implementation : http://ideone.com/kOYLeZhope it helps !