Я скоро засабмичу свои решения и положу здесь ссылки.
В некоторых разборах приведены дополнительные челленджи, над которыми можно поломать голову. Делитесь идеями в комментариях. =)
Если прибавить к числу 1, его двоичная запись поведет себя понятным образом: все младшие единицы превратятся в нули, а следующий за ними ноль станет единицей. Найдем длину максимального суффикса из единиц, пусть она равна l. Тогда ответ равен l + 1, кроме случая, когда вся строка состоит из единиц, тогда ответ l.
Забавно, что в задаче div1E тоже приходится думать о том, что будет, если прибавить к числу 1. =)
Наилучшая стратегия такова: для каждого непрерывного отрезка из непрочитанных писем откроем первое письмо, пролистаем до последнего в том же отрезке, если есть еще непрочитанные письма, вернемся к списку.
Легко показать, что лучше мы сделать не сможем: для выбранного отрезка посмотрим на момент, когда мы прочитаем последнее письмо из него. Если мы еще не все прочитали, нам придется либо вернуться в список, либо переместиться в одно из соседних писем, среди которых нет непрочитанных. Таким образом, Для каждого отрезка, кроме одного, мы должны совершить лишнее действие, которое не приводит к прочтению нового письма. Эта же оценка достигается, если действовать по описанному выше методу.
Если строка s содержит нетривиальную подстроку-палиндром w, то она содержит и подстроку-палиндром длины 2 или 3 (к примеру, это середина строки w). Поэтому строка s является терпимой тогда и только тогда, когда никакие два соседних символа или символа через один не совпадают.
Найдем теперь лексикографически следующую терпимую строку t. Она больше, чем s, поэтому у них есть общий префикс (возможно, нулевой длины), и следующий за ним символ больше в t, чем в s. Кроме того, этот символ должен располагаться как можно правее, чтобы строка t была как можно меньше. Для каждой позиции i мы можем попытаться увеличить si и проверить, не совпадает ли он с si - 1 или si - 2. Если у нас получилось сделать так с каким-то символом, оставшийся суффикс всегда можно корректно дополнить, если выполняется условие p ≥ 3, поскольку при заполнении его слева направо у нас всегда не больше двух запрещенных символов. Каждый символ в суффиксе надо жадно делать как можно меньше, чтобы не создать конфликтов с тем, что уже есть слева. Пишем жадность или умный перебор, они работают за O(n). Случаи p = 1 и 2 разобрать нетрудно, потому что в первом случае подходит только a, а во втором только a, b, ab, ba (впрочем, если жадность правильная, их и разбирать особо не надо).
Это пример общего алгоритма для генерации лексикографически следующего чего угодно: попытаемся увеличить элемент в позиции, расположенной как можно правее, чтобы суффикс можно было добить как-нибудь, после этого добиваем суффикс минимальным способом.
К сожалению, оказалось, что это более простой вариант задачи, которая уже встречалась на одном из старых раундов: 196D - Следующая хорошая строка. Мы не были в курсе этого и приносим за это свои извинения. В счастью, похоже, никто не стал копировать оттуда решения. Если вам понравилась эта задача, можете попытаться решить ее усложненный вариант. =)
Для этой задачи есть куча способов решения. Опишем самый лобовой: переберем все перестановки координат для каждой точки, и для всех конфигураций проверим, является ли данное множество точек вершинами куба. Количество различных конфигураций в худшем случае можно достигать (3!)8 > 106, поэтому проверка должно работать быстро.
Проверять можно, например, так: найдем минимальное расстояние между всеми парами точек, оно должно быть равно длине ребра куба, обозначим его за l. Для каждой вершины должно найтись ровно три другие вершины на расстоянии l, и ребра, исходящие в эти вершины, должны быть попарно перпендикулярны. Если это выполняется в каждой вершине, наша конфигурация является кубом, поскольку не-куб в таких условиях построить нельзя. Такой способ выполняет примерно 82 простых операций на каждую проверку, что достаточно быстро. Существуют и другие способы проверки, опирающиеся на различные свойства куба.
Такой алгоритм можно по-разному оптимизировать, чтобы наверняка влезть в TL. Можно, например, заметить, что если переставить все координаты каждой вершины куба одинаковым образом, получится снова куб. Отсюда заключаем, что порядок координат любой одной точки можно фиксировать и перебирать только остальные. Эта простая оптимизация ускоряет алгоритм в 6 раз, что сильно облегчает задачу упихивания во время.
Челлендж: судя по всему, работает и такой способ проверки: найдем длину стороны l, и посчитаем количество пар на расстоянии l, 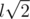 ,
, 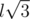 . Куб должен содержать ровно 12 пар первого типа, 12 пар второго типа и 4 пары третьего типа. Можете ли вы доказать, что это необходимое условие является достаточным для того, что конфигурация является кубом? Верно ли это, если координаты могут быть нецелыми? Можете ли вы придумать еще более простой способ проверки на куб?
. Куб должен содержать ровно 12 пар первого типа, 12 пар второго типа и 4 пары третьего типа. Можете ли вы доказать, что это необходимое условие является достаточным для того, что конфигурация является кубом? Верно ли это, если координаты могут быть нецелыми? Можете ли вы придумать еще более простой способ проверки на куб?
Хранить всю строку после каждого запроса тяжело, потому что ее длина растет экспоненциально и запросы меняют ее сложно предсказуемым образом. Иногда помогает мудрая мысль: не можешь решить задачу, попробуй решить с конца. =)
Пусть для последовательности запросов мы знаем для каждой цифры d, в какую строку превратится после выполнения всей последовательности (обозначим ее за td). Тогда строка s = d1... dn превратится в строку td1 + ... + tdn (+ означает конкатенацию). Обозначим за v(s) числовое значение строки s. Тогда v(s) можно выразить как v(tdn) + 10|dn|(v(tdn - 1) + 10|dn - 1|(...)). Поэтому, чтобы найти v(s), достаточно знать md = v(td) и sd = 10|td| для всех цифр d. Раз ответ нужен по модулю P = 109 + 7, сохраним все эти числа по модулю P.
Теперь добавим спереди к последовательности новый запрос di → ti. Как поменяются чиселки md и sd? Очевидно, для d ≠ di ничего не поменяется, а для di их надо пересчитать по формуле выше. Это делается за время O(|ti|). Когда добавили все запросы, ответ для исходной строки s вычисляется точно так же за время O(|s|). Получили решение за 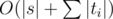 . Код по сути состоит из одной формулы, поэтому реализация получается проще некуда.
. Код по сути состоит из одной формулы, поэтому реализация получается проще некуда.
Тупые решения, которые просто хранили всю строку и честно выполняли запросы, могли случайно проходить претесты. Очень жаль.
Челлендж: пусть мы хотим выдавать ответ после каждого запроса. Это легко делать off-line за суммарное время O(n2). Можно ли быстрее? Что, если мы обязаны отвечать онлайн?
В этой задаче надо было хорошо понимать вероятность, но в остальном все тоже несложно.
Обозначим количество заработанных монет X, а количество монет за продажу только предметов типа i за Xi. Понятно. что X = X1 + ... + Xk, и EX = EX1 + ... + EXk (здесь EX это мат. ожидание X). Поскольку все типы имеют равную вероятность выпадения, все EXi равны между собой, и EX = kEX1. Давайте искать EX1.
Если следить только за предметами одного типа, например, 1, выпадение предметов выглядит так: с вероятностью  нам ничего не выпадает, а с вероятностью
нам ничего не выпадает, а с вероятностью 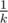 мы получаем предмет, уровень которого распределен как обычно. Обозначим за dn, t среднее количество заработанных денег после убийства n монстров, если в начале у нас есть предмет уровня t. Ясно, что d0, t = 0 (убивать больше некого, и денег мы не заработаем), а
мы получаем предмет, уровень которого распределен как обычно. Обозначим за dn, t среднее количество заработанных денег после убийства n монстров, если в начале у нас есть предмет уровня t. Ясно, что d0, t = 0 (убивать больше некого, и денег мы не заработаем), а 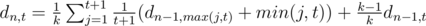 , что то же самое, что и
, что то же самое, что и 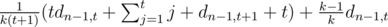 =
=  . Ответ находится как EX1 = dn, 1. К сожалению, у этой динамики Ω(n2) состояний, что слишком много при
. Ответ находится как EX1 = dn, 1. К сожалению, у этой динамики Ω(n2) состояний, что слишком много при 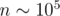 .
.
Можем ли мы поотсекать маловероятные события, которые не сильно влияют на ответ? Мы видим, что вероятность улучшить наш предмет падает с ростом его уровня, поэтому вряд ли он может стать очень большим. Мы знаем, что среднее количество попыток до успешеного выпадения монетки с вероятностью выпадения p равно 1 / p. Поэтому, среднее количество монстров, которых надо убить, чтобы получить предмет уровня T, равно 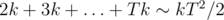 . Поэтому в общем случае уровень нашего предмета будет равен примерно
. Поэтому в общем случае уровень нашего предмета будет равен примерно 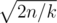 , что в наших ограничениях не превосходит 500. Мы хотим найти такую границу B, что если отсечь все состояния при t > B, ответ изменится не сильно. Это можно сделать, если честно посчитать дисперсию T и применить какое-нибудь неравенство типа Чебышева, или установить опытным путем: если мы увеличили границу, а ответ не поменялся, значит, она уже достаточно хорошая. На практике оказывается, что B ≥ 700 хватает для заданной точности. Получили решение за время
, что в наших ограничениях не превосходит 500. Мы хотим найти такую границу B, что если отсечь все состояния при t > B, ответ изменится не сильно. Это можно сделать, если честно посчитать дисперсию T и применить какое-нибудь неравенство типа Чебышева, или установить опытным путем: если мы увеличили границу, а ответ не поменялся, значит, она уже достаточно хорошая. На практике оказывается, что B ≥ 700 хватает для заданной точности. Получили решение за время 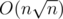 (мы опираемся на то, что
(мы опираемся на то, что 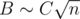 , и константа C спрятана в О-большом).
, и константа C спрятана в О-большом).
Челлендж: пусть мы убиваем монстров и предметы выпадают по тем же правилам, но теперь мы каждый раз можем выбрать, хотим мы продать новый предмет или уже имеющийся того же типа. Мы хотим максимизировать количество монет в конце. Каково мат. ожидание этого количества, если мы действуем оптимально?
Теперь иногда выгодно продавать дорогой и крутой предмет, а иногда выгодно оставить себе. Насколько быстрое решение такой задачи вы сможете придумать?
Это было бы просто упражнение на графовые алгоритмы, но непонятно, как работать с большими весами ребер, которые надо складывать и сравнивать абсолютно точно.
То, что вес каждого ребра — это степень двойки, подсказывает нам, что можно хранить битовую запись длины пути, поскольку она не сильно меняется при добавлении одного ребра. Но хранить все записи явно для всех вершин нельзя, поскольку суммарное количество единиц в них Ω(nd) (где d — это максимальное значение xi), что не влезает в память даже с битовой магией.
Хочется воспользоваться какой-нибудь полезной структурой. Хорошо подходит персистентное дерево отрезков, которое хранит битовую запись. Персистентное дерево отличается от обычного тем, что каждый раз, когда мы хотим поменять состояние какой-то вершины, мы вместо этого создаем копию этой вершины и записываем новые значения в нее. Теперь у нас есть что-то вроде <<системы контроля версий>> над деревом: все состояния каждой вершины, и к любой вершине можно делать запросы, поскольку все ее поддерево, достижимое по ссылкам, остается неизменным. В таком дереве все запросы все еще выполняются за  времени, но каждый запрос может потребовать создания
времени, но каждый запрос может потребовать создания  дополнительных вершин.
дополнительных вершин.
Какие запросы к дереву мы хотим делать? Чтобы прибавить к числу 2x, нужно найти ближайший ноль к x-ой позиции, записать в него единицу и заполнить нулями все позиции от него до x. Это умеет делать дерево с ленивым проталкиванием, которое тоже можно сделать персистентным.
Сравнивать два числа можно так: найдем самый старший бит, где числа отличаются, тогда то число, у которого в этом бите записан 0, меньше; если никакие биты в числах не различаются, они равны. Это можно делать за  , если хранить хэши поддеревьев в каждой вершине и параллельно спускаться по обоим деревьям. Ограничения по времени и памяти были очень добрыми, поэтому разных хэшей можно было хранить сколько душе угодно и не бояться коллизии.
, если хранить хэши поддеревьев в каждой вершине и параллельно спускаться по обоим деревьям. Ограничения по времени и памяти были очень добрыми, поэтому разных хэшей можно было хранить сколько душе угодно и не бояться коллизии.
На этом общая идея заканчивается. Теперь просто используем такую реализацию чисел как черный ящик внутри Дейкстры. Все операции с числами замедлились в 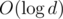 , поэтому наше решение работает за время
, поэтому наше решение работает за время 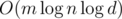 . Однако, реализовывать его надо было аккуратно.
. Однако, реализовывать его надо было аккуратно.
Главная ошибка, которую можно было сделать — сравнивать числа за 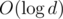 дополнительной памяти, поскольку чтобы спускаться по дереву, нам иногда приходится делать проталкивания, и это создает новые вершины. Если так делать, мы съедим
дополнительной памяти, поскольку чтобы спускаться по дереву, нам иногда приходится делать проталкивания, и это создает новые вершины. Если так делать, мы съедим 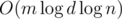 памяти, что в ML уже не влезает никак. От этого можно избавляться по-разному; например, если мы приходим в вершину, из которой надо что-то протолкнуть вниз, это значит, что весь отрезок этой вершины состоит из одинаковых чисел, поэтому ответить на запрос о сравнении можно уже сейчас.
памяти, что в ML уже не влезает никак. От этого можно избавляться по-разному; например, если мы приходим в вершину, из которой надо что-то протолкнуть вниз, это значит, что весь отрезок этой вершины состоит из одинаковых чисел, поэтому ответить на запрос о сравнении можно уже сейчас.
Я хочу описать, как мне кажется, самое изящное решение по времени, памяти и простоте кода, которое позволяет совсем избавиться от ленивого проталкивания. Сперва создадим два дерева, полностью заполненных нулями и единицами соответственно. Пусть теперь мы присваиваем что-то на отрезке (пускай, для определенности, ноль), и текущая вершина целиком лежит внутри отрезка из запроса. Теперь вместо того, чтобы создавать копию и/или проставлять какие-то пометки, заменим эту вершину на соответствующую вершину из дерева с нулями. Все, поддерево этой вершины заполнено нулями, как мы и хотели. Если так делать, каждая операция создает  новых вершин (с ленивым проталкиванием такого достичь не удастся, придется создавать минимум
новых вершин (с ленивым проталкиванием такого достичь не удастся, придется создавать минимум 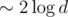 ), кроме того, вершины хранят в себе меньше информации и занимают меньше памяти. И про проталкивание чего бы то ни было думать не надо. Красота.
), кроме того, вершины хранят в себе меньше информации и занимают меньше памяти. И про проталкивание чего бы то ни было думать не надо. Красота.
К этой задаче челлендж отсутствует, она и так достаточно challenging. =) Эта задача — хорошее упражнение, если вы хотите научиться работать со сложными структурами, поэтому всячески рекомендую ее написать и сдать в дорешку.
Все. Если остались вопросы, не стесняйтесь спрашивать в комментах. Благодарю за внимание.










What's the greedy approach to solve 464A - Нет палиндромам!?
Round #265 was my first contest here at Codeforces and I enjoyed very much participating in it, in a large part due to the varied analytic approaches considering all problems. The contest's problemset at Div. 2 didn't demand pulling off very advanced algorithms but, first of all, some careful observation and coding in a straighforward manner so that the round time would be well spent.
I thought that clearing problem D, even instead of its easier conterparts B and C, would fit in a reasonable round strategy since checking its entire search space for solution correctness is straightforward. However, I had a more of a hard problem trying to fit my Java solution under a doable time limit and I also took too much time modifying my solution's code in place of the algorithm itself, so had I opted for an "easy" algorithm speed-up such decision would pay off dearly.
464A — No to Palindromes's editorial is not detailed enough. there are two things to be done: 1. keep palindrome 2. next minimal string t the first thing, the editorial says just keep checking t[i] != t[i — 1] && t[i] != t[i — 2], that's ok. but the second thing and the whole process is not clear enough. can someone explain it more clearly?
let's look at the a little bit changed last example given in the problem:
n = 4, p = 4, s = bacdif we want to find lexicographically next string we should start to change right most char (d). but it can't changed because p = 4 and we can just use a, b, c, d. so we try to change the char at the left of the right most char (c). we increase it and we get d and we delete all of the chars that comes after this char and we get:bad_after this we try to fill the deleted part of the string with a string that is as possible as lexicographically small. so we try to put a and we get:badathis is not a valid string because "ada" is palindrome. lets try b:badbyes we found.i hope this will help.
And also for filling the deleted part,on average you need O(n) time,because for every j from i+1 to n,you want to put the lowest letter != s[j-1] and != s[j-2],and this will take at most 3 steps. :) This is why the total complexity is O(n^2 * 26).
excellent
can someone provide a better explanation to 464C — Substitutes in Number ?
There are two things we need to keep track of for each digit: the value it will eventually turn into, which we can keep modulo 10^9+7, and the length of the number. With just these two values, we can apply rules efficiently. Keep track of these in two arrays val, len
Our base case is just that each digit goes to itself and has length 1. (i.e. val[i] = i, len[i] = 1).
Now, let's focus on applying a single rule of the form p -> d_1d_2...d_n
Notice applying these rules takes time linear to the number of characters in the rule, so applying all rules will take O(|t|) time.
Now, apply rules from the end of list to the front of the list until we get to the first rule. To get the final answer, just add a rule 0->s to the front, and return val[0]. Total running time is O(|s|+|t|).
You need to be careful with mods, but you can also notice you should mod the lengths of numbers by (10^9+6) since we're taking 10^len, and we know 10^len mod 10^9+7 = 10^(len mod 10^9+6) mod 10^9+7 by Fermat's little theorem. Of course, instead of storing len, you can just store 10^len directly, and you can adjust the rules and base case above as necessary. This way doesn't require FLT, and is what the editorial is referring to.
Hopefully this helps, this is a brief overview on how to solve.
Why do we need to process the queries backward from the end to the front? UPD: Sorry for a naive question, I got it!. Your explanation is clear for me now!
thanks :)
can u help me find why my submission return a TLE. thank u.http://mirror.codeforces.com/contest/465/submission/7749873
Source of TL (if it was not TL, it would be WA):
gets stuck in infinite loop, when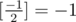 .
.
expis negative, becauseYour problem is next:
len[i]can grow exponentially, so if you are not careful, it will overflow long long type, and probably will be negative at some point.But because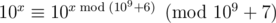 (see Fermat's little theorem), you can store
(see Fermat's little theorem), you can store
len[i]modulo 109 + 6: 7750490. Only change is lineu r right!thank u!
thanks a lot! :)
Спасибо большое за div. 1 C! Мне действительно понравилось решать её :)
It seems like there is a typo in the explanation of the Div2.E/Div1.C.
The resulting number is written to be represented as
v(tdn) + 10^|dn|*(v(tdn - 1) + 10^|dn-1|*(...)), however, it seems like it must bev(tdn) + 10^|tdn|*(v(tdn-1) + 10^|tdn-1|*(...)).For example, lets
s=01initial string, if substitutions are0->23and1->45, then the resulting string iss=2345, according to the formulav(s) = 45 + 10^|1|*23which is incorrect.В этом раунде сложнее было реализовать, чем придумать (A, B, C div.1)
Did anyone manage to get an AC in the problem 464B — Restore the cube by coding in Java?
I implemented the brute force approach mentioned in the editorial in Java but got a TLE: Java Solution
Any ideas on speeding up the solution?
Have you tried not to shuffle first point?
I haven't but I can. Could you please explain in more detail the correctness of the solution if the first point is not shuffled?
Suppose you found a cube. Shuffle coordinates of all points in the same way so that first point will stay the same. Cube will be still a cube because coordinates are independent.
I tried your suggestion, but sadly I get a WA: Modified Java submission
Although, I get the correct answer with my previous code. Am I doing something wrong?
Hi Alex, I figured out the mistake in my code. I managed to get an AC after keeping the first point constant. Thanks a lot!
AC Solution
Hi sultan, I am still not able to figure out why we need to fix one point and shuffle only others.
Could you please help me understanding that?
Hi, we can fix one point and find the other points by shuffling. If a cube is possible then we'll know, no need to shuffle the fixed point.
To fully understand this, I think it'll help if you visualize/draw the figures on paper.
The way I understood it was by reducing the 3d cube to a 2d rectangle. Take any rectangle in the 2d plane, start with axis parallel rectangles. Now keep one point fixed. Swap (x,y) coordinates of the rest of the 3 vertices. You'll again get a rectangle of the same length and breadth. Go ahead, draw it on paper and see for yourself.
Similar concept can be applied to the 3d cube, when we ensure that the coordinates are shuffled in the same way i.e. for e.g. swap x and y of all vertices except one, the resulting 3d figure will still be a cube of the same dimensions. Similarly, it holds true if you swap y and z, z and x, etc
I hope I was clear enough :)
Что за раунд, что за разбор тебе надо памятник поставить при жизни.
464E — The Classic Problem
Memory problem can be avoided by keeping 32 bits in leaf node. Then no other tricks are needed, and you can add 2^x brutally (add 2^x to the corresponding leaf node, if it overflows add 1 to the next leaf node and so on).
We can also have perfect hashing by numbering vertices like in checking tree isomorphism.
Solution
Not true, this can result in quadratic complexity, for example your code with test generator on ideone.
The idea of test: the graph is a tree that consists of
i.e. edge
i.e. edge
Find the shortest path from 1 to 100'000.
Here, updating the shortest path to the vertices with numbers from 50 001 to 99 999, you will perform 50 000 adds of 2x for every vertex.
That's right, my mistake, thanks.
why can't it be solved by kruskal?
Что означает "добить суффикс как-нибудь"? В задаче 464A.
Скорее всего, сделать суффикс как можно меньше
Кажется, в разборе задачи Div 1 D есть небольшая ошибка: в формуле для dn, t не учитывается, что при выпадении предмета не того типа, что мы ищем, деньги, которые были у нас до этого остаются:
в разборе:
правильно:
UPD. Уже исправлено.
Верно, спасибо.
In problem A I forgot that the given string didn't contain palindroms and still get AC. The algorithm does the following:
Iterate from i=0...size(s)-1
a. Check if s[i]==s[i+2], if yes:
--> s= next substring s[0...i+2] (so p=3 a c b c a a c c a a)
a c c a a)
--> go back to the earliest position modified by the update-2.
b. else check if s[i]==s[i+1], if yes do sth analogous.
Do you think tests weak, that the condition could be removed or that the condition makes my algorithm run in time?
Thanks!
WARNING: I'm new to probability theory, so my post may not be the smartest post here, but I'm curious:
In div1 D (464D - World of Darkraft - 2), why can't the Coupon Collector's Problem be applied?
EDIT: I realize now that probably it doesn't apply, as the expectations are not independent (probability of getting level X depends on probability of getting X - 1)
Div1C.
Первая часть разбора по этой задаче понятна. Не мог бы кто-нибудь объяснить, что значит — "Теперь добавим спереди к последовательности новый запрос..."? И не совсем понятна идея с обратным порядком просчёта всего этого дела.
Спасибо.
Идея такова: в любой момент времени мы хотим знать для каждой цифры остаток числа, на которое мы её заменим и длину этого числа. Допустим, у нас есть такая информация в момент выполнения запроса k. Давай научимся обновлять для момента выполнения запроса k-1. Будем идти по числу из запроса и на ходу заменять в нём цифры. Это будет иметь примерно такой вид:
Наконец, целиком обработав запрос, мы точно знаем, на что мы заменим цифру, соответствующую этому запросу. Изменим значения to и len для соответствующей цифры, а остальные оставим без изменений. Теперь мы знаем, на что поменяются цифры, которые мы захотим использовать в следующем (т.е. более раннем) запросе. Идём так, пока не обработаем все запросы.
Круто! Спасибо! Разобрался.
464B — Restore Cube , In the editorial , it is written "Is it true if we allow points to have non-integer coordinates?".
What does he mean by this? I am getting WA on test case 15 ( it contains a lot of negative integers ). Here is the link to my code ( in java ) : http://mirror.codeforces.com/contest/465/submission/7737985 Can anyone help ??? Thanks in advance.
i am quite confused about the The Classic Problem,since it too strange for the modify and push
464E — Классическая задача
TL&DR: неполные тесты.
Я в этой задаче при сложении вместо того чтобы искать ближайший 0 слева, полагался на последовательный перенос (если текущий разряд равен единице, заменить его на 0 и увеличить следующий разряд), и на то, что амортизированное число необходимых переносов — O(1).
Можно заметить, что амортизированные оценки обычно ломаются для персистентных структур данных, так что мое решение не должно работать. Однако, существующие тесты эту проблему не обнаруживают!
Вот генератор теста, который убивает мое решение (7789804):
К счастью, есть трюк, который позволяет вернуться к амортизированному O(1) (7789945), но к сожалению этот трюк не пригодился.
464E - The Classic Problem
TL&DR: The tests are not complete.
In this problem when adding bits to large numbers instead of searching for the closest 0 to the left I relied on ripple carry and the fact that it's amortized O(1).
You might notice that amortized complexity usually doesn't work for persistent data structures so my solution is supposed to be quadratic. However, the existing tests do not reveal this problem.
Here is a test generator that kills my initial solution (7789804):
Fortunately, there is a trick that lets you recover the amortized O(1) (7789945). Unfortunately this trick doesn't improve your time on Codeforces.
But ripple carry is amortized when you accumulatively keep incrementing the same number but in this problem you might need to increment the same number by the same amount, i.e. do exactly the same operation, many times and then your cost is not amortised. Unless maybe you do some sort of caching--is this what your "trick" is? And did I describe the same reason for which you think your initial solution is supposed to be quadratic?
Can someone please tell me why I am getting Runtime Error using this code: http://ideone.com/8m5Bve Problem is C. Substitutes in Number. Codeforces Round #265 (Div. 1)
Can someone provide a prove for those conditions in 464B — Restore Cube will form a cube and not the different thing?
Is there a solution for the challenge part of 464C — Substitutes in Number?
If someone could comment on a possible solution to the challenge part of 464C, that would be great!
464E — The Classic Problem
Why do you need a tree containing only 1's? I used your "clever trick", which I like, but I only needed a tree containing only 0's.
can anyone please clear my doubt in
464A No to Palindrome? Suppose we find a position 'i', and increase the corresponding char s[i] such that s[i] != s[i-1] and s[i] != s[i-2]. Now consider the prefix s[0:i+1]. How can you guarantee/prove that there exists a tolerable string with s[0:i+1] as its prefix ?Endagorion ?