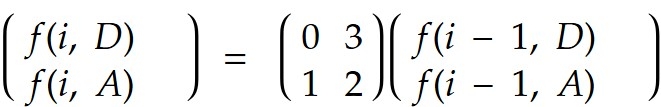Link to the problem You are given a tetrahedron. Let's mark its vertices with letters A, B, C and D correspondingly.
your task is to count the number of ways in which the ant can go from the initial vertex D to itself in exactly n steps. In other words, you are asked to find out the number of different cyclic paths with the length of n from vertex D to itself. As the number can be quite large, you should print it modulo 1000000007 (1e9 + 7).
Idea is simple,
Base case?
For a general i?
Think a little bit (relation between A, B and C)
Use the above mentioned recursive relations to find out the answer
Code
Optimized code can be found here (DP solution Click here for code)
What if n<= 1e18? Think about the optimizing the above equations in matrix form, u might have done this for fibonacci series
Further optimized code (Click here for code)
Solutions are discussed in this video