Условие :
Я умею решать за n * n / 32. Сначала, идем и ищем маленький массив как подстроку, потом битсетами берем xor и все хорошо.
После 25 попыток я понял что мне не загнать такую асимптотику ;)
На timus писали что-то про FFT, но как его туда впихнуть, не понятно.
Прошу помощи.











Там сводится к скалярным произведениям, а как их находить, можно почитать на емаксе.
Здорово :)
Почитаю. Благодарю.
Лично у меня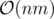 недавно (не больше месяца назад) зашло на тимусе (точнее упихнулось, возможно тесты слабые). Здесь тоже заходит за 998 миллисекунд.
недавно (не больше месяца назад) зашло на тимусе (точнее упихнулось, возможно тесты слабые). Здесь тоже заходит за 998 миллисекунд.
Идея с FFT такова: нам даны два массива битов: a0, ..., am - 1 и b0, ..., bn - 1, n ≤ m. Надо уметь находить для всех "разрешённых" k на отрезке [0, m - n] и выбрать среди них минимум. Пусть сi = am - i при
для всех "разрешённых" k на отрезке [0, m - n] и выбрать среди них минимум. Пусть сi = am - i при  . Тогда
. Тогда
А второе выражение уже почти представляет из себя коэффициент какого-то произведения многочленов при m - k. Только XOR вместо произведения. Это легко исправить: Пусть Ci = ( - 1)ci, Bi = ( - 1)bi. Тогда если ci = bj, то Ci·Bj = 1, иначе Ci·Bj = - 1. Пусть F — многочлен с коэффициентами Ci при xi, G — многочлен с коэффициентами Bi при xi. Тогда можно посчитать FG за с помощью FFT. Тогда заметим, что если коэффициент FG при xm - k равен t, то
с помощью FFT. Тогда заметим, что если коэффициент FG при xm - k равен t, то  .
.