Всем привет! Первый раунд опенкапа закончился. Давайте обсудим задачи.
UPD. Результаты раунда — http://opentrains.snarknews.info/~ejudge/res/res10271
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Всем привет! Первый раунд опенкапа закончился. Давайте обсудим задачи.
UPD. Результаты раунда — http://opentrains.snarknews.info/~ejudge/res/res10271
| Название |
|---|



Я к сожалению сегодня писал один и всего 2 часа. Так и не смог побороть Б. Считал все в дробях, дроби сокращал, но что то видимо не учел.
Может есть какие идеи, где стандартно мог проколоться?
Вообще, там нужно пользоваться тем, что ни одна дробь не превосходит 1, но строго больше нуля. Считая в лоб мы можем натолкнуться на последовательность с 100000 простыми числами, где ни сокращение дробей, ни длинная арифметика уже не помогут.
Контест было лень писать, но разве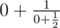 не превосходит единицу?
не превосходит единицу?
В условии написано, что ai > 0 при i > 0, поэтому такой случай невозможен.
А, ладно, я таки не умею читать условия. Но все-таки нехорошо писать в формате вывода |ai| < 109 и больше ничего, ведь именно на этом акцентируется основное внимание
Так написано же в двух местах: и в условии, и в формате ввода (сразу после |ai| ≤ 109).
Если такие ограничения не вводить, не будет однозначного представления для рациональных чисел (это, кстати, тоже написано).
Подскажите решение C и I из div1. в I поток надо пихать?
В I есть решение без потока динамикой за O(nm)
Можешь рассказать?)
Основная фишка — что граф ациклический, так что топологически его отсортируем и будем считать, что все дуги идут слева направо. Будем строить пути одновременно. В каждый момент есть текущая вершина на пути из A в B и текущая вершина на пути из C в D. Будем двигать ту из них, которая левее.
Это решение находит просто два пути. А чтобы они рёберно не пересекались, нужно добавить к состоянию ещё один бит: верно ли, что мы только что пришли из состояния, где две вершины были равны. Если да, то сразу же идти опять в такое состояние нельзя.
Состояний O(N^2), переходов в сумме O(N*M).
А как решать потоком?
Можно не добавлять бит, а двигать оба пути одновременно из состояний, где вершины равны. Сложность от этого не испортится.
Тогда сложность станет O(M^2). Разве не так?
Нет, будем сумма квадратов степеней вершин, что не превосходит O(NM).
Все понял, туплю. Ведь кратных ребер нету в графе
Никак, нет способа заставить поток течь именно из A в B, а из C в D.
Как-то зашёл минкост в котором сделал цену прямых ребер 1,а обратных 100000000.
И у двух ребер сделал цену. S>C = 200000000,D>T = 200000000
А можно подробнее? Минкост с не кососимметричной матрицей цен это что-то странное
Ну помимо того что я таким образом задаю ребра, я при восстановлении ответа для первого пути запрещаю проходить по ребрам S>C и D>T. А так просто минкост Белманом. И если не находит поток нужной величины или не получается восстановить оба пути то вернуть NO.
Тест приведенный ниже оно проходит.
UPD: нашёл тест на котором всё же не работает.
Судя по всему, это заходит по той же причине, что и это решение. Контртест против него есть ниже.
Во втором дивизионе по I зашло такое: найдём кратчайший путь до одной пары, удалим все рёбра этого пути, найдём кратчайший до другой пары. Если не нашлось, поменяем пары вершин местами и повторим.
Вроде в первом дивизионе условие не отличается.
Кажется, контртест:
16 18
1 3
2 3
3 4
4 5
4 6
5 7
6 7
7 8
8 9
8 10
2 11
11 12
12 13
13 6
5 14
14 15
15 16
16 9
1 9 2 10
Любой кратчайший путь из 1 в 9 проходит через 8 (единственная смежная с 10 вершина) и перекрывает все пути из 2 в 10, а любой кратчайший путь из 2 в 10 проходит через 3 (единственная смежная с 1 вершина) и перекрывает все пути из 1 в 9.
В то же время ответ: 1-3-4-5-14-15-16-9, 2-11-12-13-6-7-8-10.
Действительно. Моя программа, получившая AC, выдаёт "NO".
В С заходит следующее решение. Покрасим каждую вершину в случайный цвет, а затем заведем очередь вершин, которые не подходят под условие задачи. На каждом шаге берем вершину из очереди и смотрим в какой цвет мы можем ее перекрасить, чтобы количество соседей с таким же цветом было не больше одного (т.к. всего соседей 5, то это всегда возможно). Затем вершину удаляем и смотрим на ее соседей, удовлетворяют ли они условию (если нет, то добавляем в очередь).
Это правильное решение. Если не красить когда можно, то можно доказать 5E итераций. Это не более, чем 12,5V. Если этого не делать, то я думаю верно 15E.
А можно, пожалуйста, доказательство в студию?:)
Ну как — на каждом шаге число рёбер, соединяющих вершины одного цвета, уменьшается хотя бы на один.
О, клево, спасибо! У нас просто была реализация чуть другая (где вершины добавлялись по одной и перекрашивалась некоторая цепочка), и мы как-то не задумывались о том, что суммарное-то число перекрасок будет ограничено чем-то небольшим.
Это кстати тоже придумал halyavin, да.
Это на самом деле довольно старый баян (теорема 1.1).
В каких случаях раскраска графа будет невозможна? Не могу доказать, что раскраска всегда существует, но и опровергнуть это никак не получается.
Полный граф на 6 вершинах не подойдет?
Нет, не подойдет, это второй семпл :)
Нет, там можно сделать по 2 вершины каждого цвета, и у каждой, очевидно, будет не больше одного соседа того же цвета
Раскраска возможна всегда, это следует из того что после каждого перекрашивания вершины, нарушающей условие, количество пар соседей одинакового цвета уменьшается.
Но ведь не всегда уменьшается. Мы можем в одном месте коллизию убрать, а у соседа добавить..
К вершине, которую мыперекрашиваем была 2 ребра ее цвета, а стало одно, следовательно кол-во ребер между вершинами одного цвета уменьшилось.
Тогда я ничего не понимаю: написал алгоритм согласно комментариям MSPA, но получаю TLE#41. http://pastebin.com/5s2g95em
На первый взгляд у вас две проблемы: 1. Вы перекрашиваете все вершины (даже те, которые удовлетворяют условию). 2. Программу можно ускорить, если принять во внимание тот факт, что после перекраски вершины, в очередь может добавится только один сосед.
Большое спасибо: исправил, получил AC 308ms 8.79Mb
Изначально в очереди все вершины, которые имеют соседа такого же цвета? Если у вершины итак только 1 сосед такого цвета,то что с ней делать? На таком шаге кол-во ребер, соединяющих вершины одного цвета, не изменится? Сортируется ли как-то очередь, может ли в очередь быть добавлен элемент, который там уже есть? Может ли быть в очередь добавлен элемент, который был из нее удален ранее?
Нет. Изначально в очередь складываются вершины, которые не удовлетворяют условию (количество соседей такого же цвета больше одного). Очередь никак не сортируется. В нее могут попасть вершины, которые там уже есть или были. Просто когда из очереди достается очередная вершина, нужно проверить, не стала ли она удовлетворять условию, если уже все нормально, то переходим к следующей.
Пользуясь случаем, хочу передать привет человеку, который написал в объяснении к задаче D числа без интового переполнения. Последний час контеста только тем и занимался, что искал где ошибка в вычислениях.
Понял только за минуту до конца контеста, но там ещё нужно было по времени упихать. В дорешку зашло.
Как решать D, H?
Наши идеи:
По D, если бы не надо было домножать на p(A) + 1, то ответ, вроде,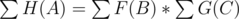 , где A, B, C итерируются по всем подмножествам U.
, где A, B, C итерируются по всем подмножествам U.
По H, утверждается, что у нас любая пара циклов если и имеет рёберное пересечение, то это какой-то элементарный путь из нуля. Значит, сперва вырезаем бесполезную часть графа (всякие деревья, отходящие от циклов), а потом выделяем циклы в виде последовательности вершин степенью три. Далее "убиваем" крайние вершины в последовательности и вершины в оставшейся части через одну.
По H: Запускаем следующий рекурсивный DFS из всех смежных с вершин, смежных с нулевой: для каждой вершины считаем количество путей в нулевую вершину, кроме того, по которому мы пришли. Если количество путей больше единицы, то значит, что это вершину нужно удалить, при этом вернув 0, иначе возвращаем количество путей. Если по окончанию DFS возвращает нам 1, то нужно удалить ту вершину, из которой мы запустили DFS.
D: Воспользуемся тем, что p(A) это сумма 2ai. Переберём i. В ответ войдут всевозможные произведения функций с множителем 2i по множествам, в хотя бы одном из которых есть i-тый элемент. Т.е. к ответу прибавляем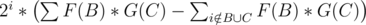
H: Отметим все вершины, смежные с 0. Теперь удалим вершину номер 0. Тогда у нас останется дерево с отмеченными вершинами. Цикл появится, если будет путь между отмеченными вершинами. А это можно сделать одним обходом в глубину жадно.
По d это наш косяк, что такое заходило. Это не планировалось, можно почистать во всех точках за n*2^n. Напишу как, когда буду не с телефона, если до этого никто не напишет. А функцию просили, чтобы со скоростью вывода не было проблем.
Мы это n*2^n упихивали в TL ногами)
Странно. У нас на плюсах 0.5 секунды, на джаве секунда. Бывает рекурсивный, он наверное подольше.
Раз никто не рассказал, давайте расскажу, что имелось ввиду.
Посчитаем такое преобразование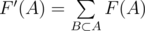 . Тогда H' = F' * G' поточечно, кроме того
. Тогда H' = F' * G' поточечно, кроме того 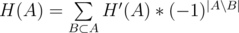 .
.
Осталось научиться быстро считать F' по F. Обратное аналогично
Это считается динамикой
,
Физический смысл dp[k,A] сумма по подмножествам в которых все элементы кроме 1..k те же, что в A.
Можно более подробно по D, что входит в суммы и как их считать.
Да и в H, что удалять из этого дерева с пометками?
В D если подставить H в результат, то получится, что нужно посчитать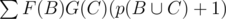 по всем B и C. Сначала избавимся от + 1. Нужно посчитать
по всем B и C. Сначала избавимся от + 1. Нужно посчитать 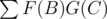 . А это считается как
. А это считается как 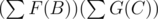 .
.
Теперь осталось разобраться с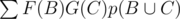 . Распишем, что такое p.
. Распишем, что такое p. 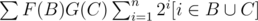 (квадратные скобки равны 0, если выражение ложно, и 1, если истинно).
(квадратные скобки равны 0, если выражение ложно, и 1, если истинно).
Поменяем порядок суммирования. Внутреннюю сумму мы можем переписать как сумму по всем B и C минус сумму по множествам, в которых i нет.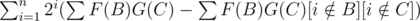 .
.
Ну и в итоге нужно ответ считать по формуле
Теперь по поводу H. Вот мы поставили отметки в вершинах, связанных с 0. Теперь забудем, что эта вершина существует, у нас останется дерево. Теперь нам нужно удалять вершины в этом дереве, чтобы в каждой компоненте было не больше одной помеченной вершины. Запустим дфс, который будет считать, сколько достижимых отмеченных вершин в поддереве. Как только получается, что в какой-то вершине набралось хотя бы две отмеченные достижимые, эту вершину нужно удалить и после обработки детей, дфс должен вернуть из неё 0.
Спасибо, очень доходчиво.
В D можно очень просто сосчитать функцию . Для этого можно просто для каждого множества сосчитать сумму значений f от всех его подмножеств и сумму значений g от всех его подмножеств и перемножить. Дальше можно методом включений-исключений перейти от q к h. Вот код, чтобы понятней было: http://pastebin.com/f5LSaXZG
. Для этого можно просто для каждого множества сосчитать сумму значений f от всех его подмножеств и сумму значений g от всех его подмножеств и перемножить. Дальше можно методом включений-исключений перейти от q к h. Вот код, чтобы понятней было: http://pastebin.com/f5LSaXZG
"Честное" решение D: Определим conv[F] как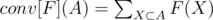 . Тогда обратный к conv оператор определяется так:
. Тогда обратный к conv оператор определяется так: 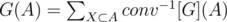 .
.
Пусть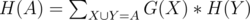 . Рассмотрим
. Рассмотрим 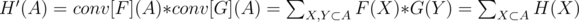 . Значит H = conv - 1[H'] = conv - 1[conv[F] * conv[G]], где * — поточечное умножение.
. Значит H = conv - 1[H'] = conv - 1[conv[F] * conv[G]], где * — поточечное умножение.
Осталось научиться считать conv[H] (и conv - 1[H]).
Определим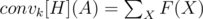 , где первые k бит X — подмножество A, а остальные совпадают с A. conv0[H] = H, convn[H] = conv[H].
, где первые k бит X — подмножество A, а остальные совпадают с A. conv0[H] = H, convn[H] = conv[H].
Тогда convk[H](A) = convk - 1[H](A) если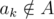 , иначе
, иначе 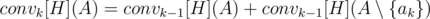 .
.
Аналогично, conv - 1k[H](A) = conv - 1k - 1[H](A) если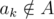 , иначе
, иначе 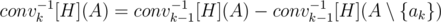 .
.
Итого, получается решение со сложностью O(2n * n): http://pastebin.com/Y2Hw2saP.
А каким образом команды в "Sponsor standings" попадают? Почему там нет половины ACM команд?
/blog/entry/14317
Выдержка из правил
4.2.4 В спонсорский зачёт каждого Гран-При входят команды со статусом ACM, участвовавшие в данном Гран-При в соответствии с 4.2.1. и выполнившие при этом предложенные организаторами спонсорского зачёта требования. Гран-При в спонсорском зачёте считается состоявшимся, если хотя бы одна участвующая в спонсорском зачёте команда успешно решила хотя бы одну задачу.
Расскажите как решать F и J?
F: у выпуклого пятиугольника всего пять триангуляций, каждая выглядит как "одна вершина, из которой торчат две диагонали". Переберем их все, для каждой проверим, что это действительно триангуляция. Я проверял так: середина каждой диагонали лежит внутри пятиугольника, диагонали не пересекают стороны и друг друга.
Можно просто проверить, что площадь 3 треугольников совпадает с площадью всего пятиугольника, ну и что они все ненулевые.
В J перебор для первых 2000 значений показал, что один из прямоугольников всегда имеет обе стороны не более 10. А второй, очевидно, должен иметь стороны как можно более близкие к квадрату. Ну и написать можно следующий перебор. Переберем обе стороны первого прямоугольника от 1 до 100. Одну из сторон второго прямоугольника от корня оставшейся части до этого же корня минус 10000. Оставшуюся сторону можно выразить через предыдущие три, если таковая вообще существует. Выбираем наилучший ответ и выводим.
100 вроде маловато чуть-чуть, например:
999999999000010001
4000000402 999999992 1000000007 89 113
У Div2 были ограничения до 109, а у Div1 до 1018.
UPD: это я к тому, что pkhaustov участвовал в Div2-версии соревнования, а Petr пишет про Div1-версию задачи J.
Действительно, у Div1 в решении та же идея (один прямоугольник — большой и почти квадрат, другой очень маленький), но реализация требует чуть большей аккуратности. В тестах (Div1) сумма сторон маленького прямоугольника бывает больше 500, а разность сторон большого — больше 1 300 000.
Эм... В той версии условий div2, что была у меня (скачана и распечатана до контеста) ограничения были до 1018.
Так вот в чём дело было — в Div2 в начале открывались не просто старые условия, а старые Div1 условия?.. Я изучу этот вопрос.
Самое интересное, что Div2 в этот раз порешали лучше, чем обычно идут наши Div2-версии. Если всё было действительно так, надо взять этот приём на заметку.
В «настоящих» Div2-условиях у каждой задачи в названии должно было быть (Division 2) большими буквами.
O_O
Я изучил этот вопрос. Действительно, был момент, когда из репозитория можно было собрать такую версию условия (в ней ещё была ошибка в ответе на первый пример, 10 вместо 12). Видимо, это и произошло.
Из хороших новостей — в этот момент другие условия, скорее всего, не пострадали.
Прошу прощения за ошибку в условии Div2.
Вот кстати да, у нас в условии была эта опечатка в семпле.
Мне кажется, что это неправильно исправить ошибку в сэмпле и не сделать броадкаст на всех участников.
И да, в ответ Бурундуку про неиспользование Полигона: вот такие, например, досадные ошибки и вкрадываются при отсутствии достаточной автоматизации.
Как решать Е?
Будем решать с конца — удалять по одному треугольнику.
Нужно, чтобы в каждый момент множество оставшихся треугольников было связно и множество удаленных треугольников было связно и связано с внешней гранью.
Второе условие проверять просто: будем поддерживать количество сторон каждого треугольника, связанных с удаленными треугольниками или внешней гранью. Если оно >=1, то треугольник можно удалять и второе условие не нарушится.
Первое условие тоже несложно. Если у треугольника уже две стороны "внешние", то он подсоединён ко всего одному оставшемуся треугольнику и его можно безопасно удалить. Если же у него одна внешняя сторона, то его можно удалить тогда и только тогда, когда у него есть хотя бы одна вершина, не находящаяся на границе внешней грани (т.е. не бывшая на внешней грани изначально и не являющаяся вершиной какого-то удалённого треугольника).
Это всё придумали halyavin и Michael, я просто примазываюсь :)
Круто! Спасибо. Правда, в дорешке такое у меня пока получает TL137:(
UPD. уже ОК, оказывается плохо делать HashMap<Long, Edge>, и считать первый аргумент как (from << 32) | to. Потому что hashmap работает долго из-за коллизий, которые возникают, когда считает хеш от лонга...
EZ Collections, EZ Life http://mirror.codeforces.com/blog/entry/14328
Я думаю тебе надо было использовать EZCollections и не париться
Задолбали форсить, такое пока не поддерживается
Можно еще добавлять грани в порядке убывания разности расстоний до внешней грани и исходной грани.
А что делать, если разность одинаковая? Можно довольно легко построить пример, на котором оно не будет работать (если можно задавать порядок посещения для тех, у кого разность одинаковая).
Можно пример? Я вроде умею доказывать, что это работает.
Пусть есть некоторый треугольник, у которого есть три соседа. Если для этих соседей разность будет одинаковая, то и для внутреннего треугольника она будет такая же. Тогда может случится ситуация, что мы добавим вначале соседей (и после этого центральный треугольник не будет соединен со всеми другими треугольниками).
Я не умею делать пример с маленьким количеством вершин, но вроде бы понятно, как сделать так, чтобы расстояние от одного треугольника до нужных трех было одинаковым.
А какое доказательство? Может проще найти в нем ошибку?:)
Да, вы правы, я умею доказывать только то, что можно брать в порядке убывания разности, но если есть равные расстояния, то надо еще понять, в каком порядке брать такие вершины. Возможно, если сортировать равные разности еще по расстоянию до внешней вершины, то это поможет.
UPD: не прочитал что многоугольник выпуклый.
Hard to understand after translating. Can you please translate the keypoints of the solution?
Key points: 1) Since the answer is always "yes", it suffices to find the last triangle we add — after that we're left with a smaller problem of exactly the same type 2) the last triangle should possess two properties: after removing it the remaining figure must stay connected, and another figure formed by the outside of original figure plus the already removed triangles must stay connected. 3) we will maintain two things: the number of edges of each triangle that is "outside", and whether each vertex is "outside". 4) for the outside figure to stay connected, it is necessary and sufficient for at least one edge of the removed triangle to be outside 5) out of those, for the remaining figure to stay connected, it is necessary and sufficient that either two edges of the triangle to remove are outside (meaning that just one edge connects it to the figure, and it can be safely removed), or one edge of the triangle is outside AND at least one of its vertices is not outside.
Как решалась задача C с покраской графа?
UPD Прошу прощения. Не обратил внимания, что выше объяснено.
Выше написано.
По задаче С wa29, пожалуйста, помогите найти ошибку: код
Кажется, самый простой способ найти ошибку в Вашем далеко не читаемом коде — это в конце проверить, верен ли ваш ответ и позапускать решение на маленьких случайных тестах.
How about G?
Play randomly until each connected component becomes small (<= 10 possible moves). After that, compute grundy function of each component in O(2^n), and xor values for all components. With high probability, result will be non-zero.
One of the solutions involves only trivial observations, but a fair bit of coding.
When we have a game position, it can be partitioned into independent regions where moves can be made. Two possible moves are immediately dependent when they share at least one cell.
We will recognize three classes of regions based on two boolean outcomes.
Is it possible to invalidate all possible moves in the region by a single move?
Is it possible to make a move such that there remains at least one possible move from the region?
An example of (1) but not (2) is a square of 2 × 2 or 3 × 3 cells. Such a region (a Type I region) requires exactly one move to disappear.
An example of both (1) and (2) is a rectangle of 2 × 4 or 3 × 4 cells. In such a region (a Type II region), we have a choice: it requires either one or two moves to disappear.
An example of (2) but not (1) is any large region. Such a region (a Type III region) requires at least two moves to disappear.
Our first goal will be to have only Type I and Type II regions left on the board. We can try to achieve a perfect grid of Type II regions (4 × 2 rectangles) by trying to place every square of the pattern shown on the left picture. Of course, Felix will mess things up, and the resulting board will look more like the right picture (result of a 16 × 20 game up to this point).
There are 8 Type I regions, 8 Type II regions and 2 Type III regions on the right picture.
In the second part of the game, we eliminate all Type III regions by detecting them and making random moves in these regions.
In the endgame, we have only X Type I regions and Y Type II regions.
If X and Y are even, the player who makes a move loses if both play optimal: the winning strategy for the other player is to keep them both even after their turn. If we find Sophia in such position, we can make a random move and hope Felix does not follow the winning strategy.
If X is even and Y is odd, we make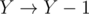 by eliminating one Type II region, so that both are even after our turn.
by eliminating one Type II region, so that both are even after our turn.
If X is odd and Y is even, we remove one Type I region just the same.
Finally, if X and Y are both odd, we move in a Type II region such that it leaves a new Type I region, effectively making the new values of X and Y even: X increases by one and Y decreases by one.
The more Type II regions we had at the beginning, the more are our chances to eventually avoid the situation when X and Y are even and Sophia has to make a move. If we avoid that at least once before the game is over, we follow the above simple strategy to win.
The above strategy is a simple case of calculating and using Grundy numbers for regions, as in winger's solution: they are 1 for Type I regions and 2 for Type II regions. Still, this solution requires only knowledge of elementary game theory and invention of simple symmetric strategies.
When checked several times against the judges' test cases with different random seeds, it won at least 293 out of 300 games.
My solution with region cutoff of <= 16 wins ~99.85% of games on 16x16 field and nearly 100% on 25x25, but unfortunately is too slow to pass the TL.
I don't have a login. How can I get the problems? Will the contest be published on gym?
when did it start
Где посмотреть задачи?
Как решать A (Barabashka, Div.2)? Или как пройти 2-ой тест? Беру сперва красный стул, потом 2,3,4 предметы совподающие, а потом немогу забрать "blue book", так как он 1 на столе остался, а на карте есть "blue bottle".
Один предмет можно брать несколько раз
Спасибо, теперь решил. А как решали B (div.2)? Мне TLE na test 37, так как использую арифметику больших числ.
Жаль, что EZBigInteger еще нет.
А вот EZ Collections уже есть! http://mirror.codeforces.com/blog/entry/14328
Вы так говорите, как будто эту задачу можно решить с помощью BigInteger.
Ведь не успеет всё равно, как его оптимально ни пиши.
Перед тем, как показывается очередная карта, все предметы ставятся на стол.
Grand Prix of Siberia в это воскресенье начнется в 11:00 по московскому времени? Просто на сайте кубка время на сервере, видимо, до перевода на зимнее время, поэтому непонятно, во сколько начнется?
Я отправил заявку неделю назад на регистрацию сектора, а open cup не отвечает. Написал пару дней назад им еще раз, все еще глухо. Хотя перед тем, как отправить заявку, я уточнял по поводу участия в кубке координатора сектора — ответили через пару часов.
Как быть? Что делать? Хочется в это воскресенье этап написать.
Данные по новым секторам будут высланы завтра.
Можно обновить расписание на оф.сайте, если уже что-то более-менее конкретно известно? Там до сих пор не указано, какой этап будет после Grand Prix of Siberia и когда вообще он будет:)