Есть известная задача для новичков которые только научились алгоритму поиска минимума в массиве: найти M минимальных в массиве из N элементов.
И вот коллега недавно проводил собеседование и троллил соискателя вариацией:
Есть десятки терабайт логов — обозначим их как
Nзаписей — каждая запись содержит в частности значение некоторого параметраA. Мы хотим выбрать небольшое количествоM(ну скажем, миллион) записей в которых значение параметра минимально. Как это сделать?
Характерные нюансы вариации:
- исходные данные живут во внешней памяти, в оперативку их целиком не прогрузишь;
- очень желательно чтобы алгоритм можно было распараллелить т.к.
Nопределяемое терабайтами близко по порядку к1e12и один проход на обычном компьютере будет занимать примерно сутки (исходный массив хранится в распределённой системе так что нет проблем с тем чтобы использовать его пофрагментно).
Собеседуемого мой коллега успешно затроллил и выгнал с позором, но потом я взялся троллить его самого — и его собственное решение ему нравиться перестало.
Какие возможны подходы к этой задаче?
У меня родилось немного "детских" версий:
Можно идти по нашим данным и пихать их в двоичную кучу с максимальным размером
M(т.е. пропускаем элемент если его параметр больше чем максимальный в куче, а если в кучу что-то запихнули и размер сталM+1то вытряхнем из неё максимальный элемент). Быстродействие здесь будет лучше чемN*log(M)потому что не придётся обычно пихать все элементы — даже вероятно ближе кN + M*log(M). Однако как распараллелить двоичную кучу? Возможно заменить её наConcurrentSkipListMap...Если само
Mтаково, что не помещается в оперативку (ещё вариация предложенная коллегой), то вместо кучи мы будем складывать элементы в список-копилку и после достижения размера2Mбудем её сортировать слияниями и обрезать размер доM. Быстродействие по-видимомуN*log(M). Распараллеливать наверное не очень легко но можно.Больше всего мне нравится вариант (против которого коллега протестует) стохастический: пройдём по исходным данным и выберем все записи значение параметра у которых ниже некоего порога
k. Как определим этот порог? Тут разные варианты — например сделаем предварительный проход по данным и выберем рандомно столько значений параметра сколько влезает в оперативку, скажем миллиард. Возьмём от них пропорциональноеM/Nколичество наименьших значений и в качестве порогаkвыберем максимальное из этих значений. Конечно в результате просеивания мы потом можем получить не совсемMзаписей — но мы можем либо заранее завысить порог, чтобы прицелиться на2Mзаписей например — и отбросить лишнее. Т.е. этот способ хорош "среднестатистически". Его сложность может быть близка кO(N)и распараллелить его вроде легко.
Но хотелось бы узнать о более остроумных вариантах — если есть какая-то удобная структура со свойствами очереди с приоритетами, которую можно распараллеливать (а то ещё держать во внешней памяти) — то первый вариант можно довести до ума?











Есть алгоритм нахождения K-ой порядковой статистики за O(N) в наихудшем случае. Делается на основе qsort с разбиением на 5 массивов, в принципе, можно его изменить и разбить на большее количество.
Если элементы во входных логах не повторяются, то найдя m-ый по возрастанию за O(N) потом идем и кладем все что меньше или равны. Если элементы повторяются, то сначала проходим и берем все что меньше, потом выбираем необходимое кол-во равных.
Алгоритм поиска должен неплохо паралелиться, т.к. он рекурсивный. Хотя тут важно какую часть мы еще можем поместить в оперативку. Описание алгоритма есть в Кормене.
Дело в том, что алгоритм K-ой порядковой статистики работает на памяти с произвольным доступом, а не на диске с терабайтом данных.
Если считать, что у нас M влазит в память, то да, идём по массиву, заполняем буфер до 2 * M, обрезаем первые M:
std::nth_element(v.begin(), v.begin() + M, v.end()); Параллелится тем, что можно разбить массив на K частей и каждую обрабатывать своим потоком. O(N)Если же M в память не влазит, а влазит только 2K элементов (2K < M), то нужно использовать что-то вроде дисковой сортировки, но не сортировать. Мерж двух кусков по 2K элементов такой: делаем первому и второму
nth_element(a, a + k, a + 2*k)пусть a[k] > b[k], тогдаfor(i = 0;i < k;++i) swap(b[i + k], a[i + k]);сноваnth_element(b, b + k, b + 2*k)теперь все элементы первых половин массивов больше всех оставшихся элементов. Будет что-то вроде O(N * log(M/K))можно написать обычную сортировку слиянием, как в GNU coreutils, но при каждом слиянии оставлять только первые M элементов
Но последниее слияние обрабатывающее N элементов мы не можем распараллелить?
ни одно слияние не будет обрабатывать больше M элементов
А ну да, я двоечник фразу не дочитал до конца.
а не, тут я перемудрил, тут степень log2(3) появляется. F(n) = 3*F(n / 2) + O(n). Тупо сортировка слиянием лучше выходит.
На прошлом московском четвертьфинале была задача: есть определенные правила генерации последовательности, сгенерируйте ее на своем компьютере и выберите K (K ≤ 105) максимальных элементов. Количество элементов последовательности было довольно большим. Ограничение на память было 8МБ. Предлагалось два решения. Первое — тупо идти по последовательности, держа при себе не более 2K элементов, время от времени пересортировывая их каким-то хитрым способом (схоже с подходами 1 и 2). Второй подход — разобьем каждое число на два блока по 16 битов, и при первом проходе запомним, сколько чисел попадает в какой блок (который первым идет). На втором проходе мы уже будем знать, какие первые блоки могут быть у этих минимальных чисел. Вроде это выглядит довольно ограниченным по памяти и даже линейной сложности.
На контесте я пытался заслать что-то наподобие третьего подхода, но ввиду кривых рук даже не отдебагал:( Да и вряд ли зашло бы.
Второе сложности N*d, где d — кол-во разрядов в числе. Обычно d ~ lg(N).
Почему? Мы же для каждого числа узнаем блок, в котором он находится за о(1),так же за о(1) мы узнаем и последние 16 битов числа. Посчитали блоки, что гарантировано входят в ответ за о(log(n)), а потом одним пробегом добрали "недостающие" числа. Не тяжело понять, что все "недостающие" числа лежат в одном блоке.
Потому же, почему и сортировка подсчетом за O(N*d), представь что у тебя числа d битные, тогда решение за N*d/64.
Я недавно наткнулся (на курсере) на описание задачи (вроде поиска пресловутых "памперсов и пива"), где наиболее частые кортежи по бигдате искали — и там подобный рандомный вариант очень восхваляли. Т.е. похоже в реальности им пользуются не очень парясь что можно часть результатов потерять.
Непонятно почему, если мы уже согласились на N × log(M), то просто не сделать бинпоиск по значению. Вроде получается невероятно простой и легко параллелящийся код.
Опять же, каждую машину можно сделать ответственной за свой кусок логов и вытащить их один раз.
самофикс: будет, конечно же, N × log(maxA)
В формулировке не хватает многих важных деталей. Задача решается на одной машине, или на нескольких? Насколько быстрый storage (может, это ssd)? Если машин несколько, насколько быстрая сеть? Рандомно ли разбиты логи по машинам?
На одной машине ничего лучше прохода с кучей не придумаешь — bottleneck всё равно диск. Если машин несколько (k штук) — то для рандомного разбиения можно достать c * m / k минимальных элементов с каждой машинки, а потом посортить их на мастере. Если про рандомность ничего не известно, то можно либо доставать по m элементов с машинки (а потом жёсткий file sort m*k элементов), либо сделать 2 прохода — на первом с каждой машинки достать порядковые статистики , на мастере их посортить, понять, где находится ответ, и на второй фазе достать по
, на мастере их посортить, понять, где находится ответ, и на второй фазе достать по 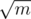 элементов с машинки. Итого — 2 прохода и 2 sort'а
элементов с машинки. Итого — 2 прохода и 2 sort'а  элементов (при этом такой подход отлично реализуется mapreduce'ом). В общем, всё зависит от требований.
элементов (при этом такой подход отлично реализуется mapreduce'ом). В общем, всё зависит от требований.
Я действительно про распараллеливание нечётко слишком сказал.
Можно считать что задача решается в реалиях хадупа — несколькими десятками виртуальных или реальных машинами, а сторадж это файлы по 100Мб в HDFS, размещённые несколькими копиями на этих машинах в произвольном порядке — т.е. да, в жизни решение именно в виде мэп-редьюса работает
да, спасибо, кажется прикольно придумано — хоть я и медленно корректность этого подхода осознаю. :)
На одной машине можно применять
nth_element(a, a + m, a + 2 * m);линия всяко лучше прохода с кучей.Это только если данные на одной машине влезают в память. Что далеко не всегда правда.