Alex7's blog

Sum of Natural Numbers
By Alex7, 10 years ago, In English

So I've just been reading that the proof that sum of all natural numbers

1 + 2 + 3 + 4... = -1/12

the mathematical proof is sound but it causes some problems like:

how come the sum of 2 natural numbers is a fraction???

my answer is because we aren't dealing with a natural finite number

but I'm not sure how to mathematically explain it

Any ideas??

(Before you rush into saying that the sum is wrong please do some research)..

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it -31 Vote: I do not like it

(Before you rush into saying that the sum is wrong please do some research)..

And only then say that the sum is wrong? Because it is — it's just a faulty result of a faulty proof. A simple example.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Why do you say so? It's counter-intuitive, but there may be some theories where assigning sums to such series have sense. For example,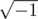 is counter-intuitive too and have no sense when using rational or real numbers, but you can extend them with complex numbers and get amazing results.

    Wikipedia article describes which methods are used to determine this value. It also notes that such methods for summation of natural numbers were used by Ramanujan and Euler, I guess they knew well what to do with numbers.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It's called "Ramanujan summation", not "summation". In other words, it's not equality in the usual sense, which is what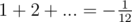 would imply. I'm not doubting it in concept of a wider theory, but if we sum up consecutive natural numbers, we don't get .

      Of course, that's the point of view of someone who's often in contact with physics, where reality is what ultimately matters.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +15 Vote: I do not like it

        Of course, that's the point of view of someone who's often in contact with physics, where reality is what ultimately matters.

        Funny that in this explanation (0:36) a professor can be heard saying «..and what's even more bizarre, is that this result is used in many areas of physics» :)

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it +15 Vote: I do not like it

          Quantum physics is weird in more ways than one :D

          Seriously, if something doesn't make sense in classical physics, it probably has an important meaning when quantum effects are introduced.

          But you're understanding it wrong — it's that the result itself is used within the bounds of a wider theory, not by itself in usual calculus (the same calculus that's used to describe classical physics).

          → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yeah, sure. I am just trying to say that this 'usual sence' is different for everyone.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it +16 Vote: I do not like it

          Nah, (almost) everyone understands summation in the same way. It's just similar (related) terminology and notation getting mixed up. And a faulty proof without zeta function.

          At least Wikipedia is watching out so it wouldn't cause confusion, putting the word "sum" in quotation marks where necessary etc. Careless reading can be dangerous, not only in math :D

          → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it -7 Vote: I do not like it

      so you're telling us that:

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +4 Vote: I do not like it

        No, that's not what I'm saying. As Xellos states, it's not 'standard summation' and never was.

        But, there is a technique called 'Ramanujan summation', which looks really like normal summation with the exception that it can assign sums for divergent series, like that one. I guess it's defined in a different way, not the way you wrote (it's like standard sums for convergent series are defined).

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it -22 Vote: I do not like it

          it's not 'standard summation' and never was.

          so you are defining a new operation which is "non stardard summation" so please give it a sign other than the plus sign "+" because when I see a plus sign "+" I expect that it is a standard summation and in standard summation simply 1+2+3... is infinity .

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
            ← Rev. 2   Vote: I like it +21 Vote: I do not like it

            The "+" sign is defined only for two operands, not for infinite number of them. What you call "summation" is a summation defined in classical calculus: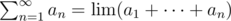 . You cannot just take infinite number of values and add them to each other; instead of it you define a symbol 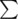and assign some meaning to it. This definition is quite intuitive and follows some basic obvious laws, such as "if you add x to the infinite series then the sum will increase by x", "{2*a_n} converges iff {a_n} converges and so on", that's why exactly this meaning is mostly used in mathematics.

            You can also define some other rule for summation. Like Lobachevsky invented his own geometry axioms, I may define some special, say, Smirnov summation: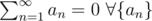 . It will fulfill only part of general rules but now all sequences will converge! One will not have to memorize difficult convergence criteria, summation could be now explained even to kids! Khhm.

            Speaking seriously, there is actually more than one way to define infinite sums. Standard calculus summation. Ramanujan summation (which you can see in this example). Cesàro summation (used in Fourier series). They are defined a bit differently and have different convergence areas but are widely used and have enough common sense in the definition.

            → Reply
»
10 years ago, # |
  Vote: I like it +39 Vote: I do not like it

We have: 1+2+3+4+... = -1/12 0+1+2+3+... = -1/12 (we just added a zero)

so if we subtract these two equations, we have:

1+1+1+1+... = 0 (perfectly logical as the first equation)

and we add it to the first equation.

=> 2+3+4+5+... = -1/12

did we just prove that 1=0?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    I guess you did something disallowed here, like subtracting two infinities or stuff. It's like Russell's paradox: if you use intuitive understanding, you can bump into contradiction. But if you use formal logic and axioms only, you won't be able to construct such paradoxical object.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    On the other hand, you proved that 2+3+4+5+...=-1/12, this means that 1+2+3+4+...=-1/12+1=11/12 (we just added 1).

    But if 1+2+3+4+...=11/12 then your proof itself is not valid, because it is based on assumption that 1+2+3+4+...=-1/12 :)

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    read this

    → Reply