Блог пользователя lukasP

NWERC 2014
Автор lukasP, 10 лет назад, По-английски

Are you coming to NWERC? Please comment in the TopCoder Forums.

There will also be an online contest. The contest starts on Sunday 2014-11-30 at 11:00 AM CET and lasts for 5 hours.

  • Проголосовать: нравится
  • +42
  • Проголосовать: не нравится

»
10 лет назад, # |
  Проголосовать: нравится +21 Проголосовать: не нравится

There will be an online contest. I have updated my post above with the correct URL and start time.

→ Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

a very good contest,i will take part in

→ Ответить
»
10 лет назад, # |
  Проголосовать: нравится +11 Проголосовать: не нравится

Is it possible to create a team for online contest? If yes, please say how.

→ Ответить
»
10 лет назад, # |
← Rev. 2   Проголосовать: нравится +8 Проголосовать: не нравится

Will ranking in online contest include teams from onsite contest? Or will we have access to ranking of onsite teams at least?

→ Ответить
»
10 лет назад, # |
← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

The online contest starts in about two hours!

→ Ответить
»
10 лет назад, # |
  Проголосовать: нравится +5 Проголосовать: не нравится

How to solve problem F, I , K ?

→ Ответить
  • »
    »
    10 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится

    I: meet in the middle on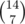 half-cycles, watch out for constants

    I suppose F is divide and conquer while bounding the number of interesting lines in a subset of points. I'm not sure what kind of bounding works, though. (UPD: Nah, I'm probably just getting the due to counting the same line many times.)

    K seemed like just efficient simulation when starting at any knapsack + computing sums for all positions from that (the time should increase linearly when moving away from a knapsack till encountering another one)... not sure, I didn't try to code it.

    → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
      ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

      I thought about the Meet in the middle technique but could not figure it out for problem I. Can you explain your idea ?

      → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
        ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

        Edit: I explained F instead :D

        Try all choices for the first N / 2 vertices of any path and remember (in a set) just the starting, ending vertex, set of vertices in the path and length of the path. The number of choices is . Backtrack, bitmasking, anything works (but the time limit is a bit tight).

        Suppose that you have two halves of a path: one between u1 and v1 and containing vertices from a set S and with length l1, the other between u2 and v2 containing all vertices not in S. Try all choices of u1, v1, u2, v2, S, l1. Try to finalize the cycle by connecting u1, v1 and u2, v2; now, the cost of the second half-path is uniquely given, so you can just check if it exists in the corresponding set.

        → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
      ← Rev. 4   Проголосовать: нравится +8 Проголосовать: не нравится

      In F p is always > 20. If line that contais > p% of points exists, then pair of randomly choosen points lies on it with probality > 0.04. So we can pick random pair of points several hundred times and either find answer or find out that it doesn't exists.

      → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
        ← Rev. 2   Проголосовать: нравится +8 Проголосовать: не нравится

        Oh, of course!

        I'm not really used to trying to find something like a randomized algorithm. I think the divide and conquer should work, but my code is getting WA somewhere. I wonder when the tests will be public...

        UPD: solved it using divide and conquer, I just missed the case when N = 1 *facepalm*

        → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
          Проголосовать: нравится +16 Проголосовать: не нравится

        Why a random pair of points? Just pick a single point, which has a 20% chance of being in the line. Count up the number of other points in each direction to check it.

        → Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

How to solve A?

→ Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Though easy problems were pretty ok, I didn't enjoy problemset in general, because 3 hardest problems were geos, no problem demanded any deeper insight (I think I figured out tricky cases in A and B, though in geo you never know) and problem "I" was really bad — I came up with good solution really quickly, but it was hard for me to squeeze it in TL, I needed 11 attempts and they differed by small optimizations.

→ Ответить
  • »
    »
    10 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    On the other hand, I think that NCPC problems were really nice :).

    → Ответить
  • »
    »
    10 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    I also made 6 attempts (though 2 of them were WA 1 -_-). In my last optimization, I realized that since it is a cycle, we can fix 1 point at 0, thus gain 7x speed up. My last submission runs in 2.25s while TL is 10s

    → Ответить
  • »
    »
    10 лет назад, # ^ |
      Проголосовать: нравится +5 Проголосовать: не нравится

    For I there are plenty of solutions that passed well below the time limit. Your approach was probably not the fastest one.

    In problem A one can come up with many "deeper inisghts" that simplify the coding. And I would also disagree on whether G was a geometry or not. It's Manhattan metric after all.

    → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
      ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

      I had complexity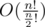 in problem I. Is there something significantly faster in terms of complexity?

      And talking about A I agree that one probably should think much before starting coding it. I started, but I quickly realized that my approach is completely wrong, because I wasn't taking care of doing a lap, which was in fact main point here. I think that we should draw two half lines with equation x = x1, y ≥ y1 and x = x1, y ≤ y1 and consider crossing them in an appropriate order (of course creating a graph of admissible connections between them and doing some dp/Dijkstra). Is that right? Even if it is then I should think about many coding issues :P. And I have to admit that this problem is really taken from "real life", which is always a plus :).

      → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
        ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

        I did a Dijkstra but I was calculating winding number instead. Try solving this problem first and then modify that approach for A. Per Austrin thinks his convex hull solution is nice too.

        The slides are up now, you can check your I solution.

        → Ответить
        • »
          »
          »
          »
          »
          10 лет назад, # ^ |
          ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

          Hah, ternary search was essential/useful in 3 tasks (B, E, G) :D. And in B it was nested ternary search :P (after seeing the editorial I have to admit that I definitely didn't consider all cases and haven't thought about ternary :P). It reminded me of a problem when I ternary searched in ternary search in order to find place where is the best result and when fixing parameters I computed result in that place using binary search :P (problem B here: http://mirror.codeforces.com/gym/100491).

          And model solution to I was essentialy the same as mine and resulted in exactly the same complexity. I would even say that my solution is more elegant, because it doesn't middle vertex and do that whole partitioning: http://ideone.com/cuWbcC It is basically Dfs considering all possible paths of length <=n/2.

          Btw sorry that in previous post I asked about is there something faster than complexity which was an expression which couldn't be parsed xD. Codeforces got down for a while, so I didn't do a preview, now it's ok :pp.

          → Ответить
          • »
            »
            »
            »
            »
            »
            10 лет назад, # ^ |
              Проголосовать: нравится 0 Проголосовать: не нравится

            E? Pfft, binsearch on the derivative.

            → Ответить
            • »
              »
              »
              »
              »
              »
              »
              10 лет назад, # ^ |
                Проголосовать: нравится 0 Проголосовать: не нравится

              Why? This is not a big difference between ternary and binary search and you do not have to do some not that nice computations about derivatives/any further thinking whether derivative is positive/negative.

              → Ответить
              • »
                »
                »
                »
                »
                »
                »
                »
                10 лет назад, # ^ |
                  Проголосовать: нравится 0 Проголосовать: не нравится

                Why? Why not? :D

                It's just that I have better skill in calculus than in coding ternary search, and if I express the original function as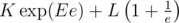 , with simple formulas for K, E, L, then I see immediately that the derivative is 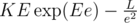— and thinking about signs is a matter of seconds (large e: positive derivative, small e: negative).

                I just pointed it out as "ha! but I'm different!" :D

                → Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

How to solve C and E?

→ Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

How to solve G?

→ Ответить
  • »
    »
    10 лет назад, # ^ |
      Проголосовать: нравится +16 Проголосовать: не нравится

    I didn't code it, but I think this should work:

    It is trivial, that if d = inf, then x *  = med(x1, ..., xn), where med is a median function and analogous property holds for y * .

    Firstly create circles with radius d for all points from input as their centers (in Manhattan metric, so in fact these are squares with sides parallel/perpendicular to y=x) and intersect them all, it will be a rectangle. If (med(X), med(Y)) lies within that field than we're done. If not, we should check all 4 sides separately (or even just 1 or 2, but doesn't matter). Each side can be checked in O(n) if we will divide it into intervals where we are not crossing x or y coordinate of any of the points.

    → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
        Проголосовать: нравится +8 Проголосовать: не нравится

      It's easier to do last step with ternary search by x.

      → Ответить
      • »
        »
        »
        »
        10 лет назад, # ^ |
          Проголосовать: нравится 0 Проголосовать: не нравится

        Good point, it surely simplifies code :) (this is not an irony, to be clear :p).

        → Ответить
  • »
    »
    10 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится +8 Проголосовать: не нравится

    You can also find rectangle in rotated plane in which solution must lie and then do 2D ternary search on it. You just have to be careful that not all points in that rectangle map to integer points in normal plane (only those with x%2==y%2 do), easiest thing to do is to do search twice, once for odd points and once for even points.

    → Ответить
»
10 лет назад, # |
← Rev. 2   Проголосовать: нравится +21 Проголосовать: не нравится

Videos of problem analysis.

→ Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

How many teams will advance to WF from this region?

→ Ответить
»
7 лет назад, # |
← Rev. 2   Проголосовать: нравится -10 Проголосовать: не нравится

Is there something wrong with problem H for the system?

http://mirror.codeforces.com/gym/101482/standings

The following simple code is not passing (WA on test 1). Am I missing something?

#include <bits/stdc++.h>
using namespace std;
#define rep(i, n) for (int (i) = 0; (i) < (n); (i) ++)
#define rep1(i, n) for (int (i) = 1; (i) <= (n); (i) ++)
#define FOR(i, a, b) for (int (i) = (a); (i) <= (b); (i)++)
#define db(x) {cout << #x << " = " << (x) << endl;}
#define dba(a, x, y) {cout<<#a<<" :";FOR(i123,x,y)cout<<setw(4)<<(a)[i123];cout<<endl;}
#define clr(x) memset(x,0,sizeof(x));
#define mp make_pair
#define pb push_back
#define sz(x) int((x).size())
typedef long long ll;
typedef long double ld;
const int INF = INT_MAX;
const ll INFL = LLONG_MAX;
const ld pi = acos(-1);
// const int MOD = ;

vector<int> G[100100];
pair<int,int> F[100100];
int T = 0;

void dfs(int u, int p, int a){
    if(p == -1){
        F[u].first = ++T;
        F[u].second = ++T;
        rep(i,sz(G[u])){
            int v = G[u][i];
            if(i == 0) dfs(v,u,F[u].first);
            if(i == 1) dfs(v,u,F[u].second);
            if(i >= 2) dfs(v,u,F[u].first);
        }
    }else{
        F[u].first = a;
        F[u].second = ++T;
        for(int v : G[u]){
            if(v == p) continue;
            dfs(v,u,F[u].second);
        }
    }
}

int main()
{
    ios_base::sync_with_stdio(0); cout.precision(15); cout << fixed; cout.tie(0); cin.tie(0);
    int N;
    cin >> N;
    rep(i,N-1){
        int a,b;
        cin >> a >> b;
        G[a].pb(b);
        G[b].pb(a);
    }
    dfs(1,-1,0);
    rep1(i,N) cout << F[i].first << " " << F[i].second << endl;

}
→ Ответить