Сегодня в 15:00 закончился November long Challenge 2014.
Давайте обсудим задачи!!!! Как решается задача POWERMUL на full?
Может кто — нибудь написать разбор в обсуждение. Буду признателен.

| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3803 |
| 2 | jiangly | 3707 |
| 3 | Benq | 3627 |
| 4 | ecnerwala | 3584 |
| 5 | orzdevinwang | 3573 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | Radewoosh | 3542 |
| 9 | jqdai0815 | 3532 |
| 10 | gyh20 | 3447 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | maomao90 | 167 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | maroonrk | 152 |
| 5 | -is-this-fft- | 151 |
| 5 | nor | 151 |
| 7 | atcoder_official | 147 |
| 8 | TheScrasse | 146 |
| 9 | Petr | 145 |
| 10 | pajenegod | 143 |
Сегодня в 15:00 закончился November long Challenge 2014.
Давайте обсудим задачи!!!! Как решается задача POWERMUL на full?
Может кто — нибудь написать разбор в обсуждение. Буду признателен.

| Название |
|---|



Решение Fomblinatorial на 40 баллов:
Предподсчитаем разложение на простые множители f(x) до 600, и при каждом запросе будем выводить ответ. Код
Мое решение примерно такое и у меня 40 баллов.
Я эту задачу не решил, но всё равно поделюсь соображениями. Сразу можно заметить, что формулу можно сократить на f(n - r). Тогда имеем
При больших r числитель и знаменатель ещё будут пересекаться в районе n / 2, и можно сократить ещё больше множителей, но я это не использовал.
Будем рассматривать каждый случай с n и m отдельно. Значения формулы можно было бы посчитать так: рассчитываем её для r = 1, потом из этого получаем значение для r = 2 и т.д. Алгоритм такой:
Большие степени по модулю будем считать с помощью двоичного возведения в степень, а inv(x) — это функция обратного элемента.
Однако это не работает, потому что не для всех значений можно посчитать обратный элемент. inv(x) существует только тогда, когда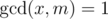 , а это не выполняется, если x|m и m > 1.
, а это не выполняется, если x|m и m > 1.
Чтобы решить эту проблему, я пробовал действовать так: разложим m на простые множители. Будем ещё поддерживать массив, который показывает, в каких степенях в результат входят эти простые множители. В шагах 4 и 5 выделим заранее из чисел n - i + 1 и i все простые множители m, запишем изменения степеней в массив (в 4 шаге степени увеличиваются, в 5 — уменьшаются), а оставшиеся от n - i + 1 и i значения теперь не будут иметь общих множителей с m, то есть, можно считать для них обратный элемент с помощью теоремы Эйлера. В конце каждого шага ещё умножим cur на произведение множителей m в тех степенях, которые записаны в массиве.
И, наконец, отвечать на запросы будем, просто выводя arr[r].
Хотя это решение, наверное, и работает, оно очень медленное, и, как я и ожидал, получило TLE. Заметим, что я так и не доказал, что результат формулы — это целое число, хоть и использую этот факт в одном месте. Наверное, если доказать это, то тогда и правильное решение будет очевидно.
Спасибо, что поделился.
Они ведь скоро выложат разборы:)
Но если лень ждать — наброски моих решений.
Distinct Characters Subsequence — понятно, что длина ответа равна числу различных букв в строке.
Let us construct palindrome — находим в строке первую позицию, на которой все портится. Так как ее обязательно нужно исправить, то понятно, что достаточно перебрать О(1) вариантов позиции (эта позиция +-1 и аналогично для ее отражения; вероятно, даже какие-то из этих лишние) — и мы можем проверить каждый из них наивно.
Chef and Segment Game — если порисовать, то понятно, что у нас сначала одна точка на первом уровне, потом две на втором, потом 4 на третьем, 8 на четвертом и так далее. А расстояние между точками на каждом уровне уменьшается в два раза. Поэтому находим по номеру точки номер уровня и позицию на уровне, дальше очевидно:)
Fombinatorial — всем знакомо решение "для простого М" — посчитать произведения по модулю, а вместо деления делать умножение на обратный элемент. Для произвольного М проблема в том, что делить уже не всегда получится:) Но если числа взаимно простые с М — то все ОК, даже если М не простое. Поэтому посчитаем все произведения в виде "часть, которая не взаимно простая с М * что-то, взаимно простое с М". Первую часть нужно считать явно, храня степени простых делителей М; вторую можно считать так, как и для простого М, предварительно сделав множитель взаимно простым с М. Например, если нужно считать 7! по модулю 24 — то это будет (2^4)*(3^2)*(5*7 mod 24). Для первой части: при умножении степени суммируем, при делении — вычитаем:) Для второй — при умножении числа умножаем по модулю, при делении — умножаем на обратный элемент. В конце считаем значение первой части по модулю (быстрым возведением в степень), вторую мы знаем, умножаем их и получаем результат:) Поскольку у числа М не может быть много различных простых делителей, то все работает достаточно быстро.
Chef and Red Black Tree — во-первых, все вершины на одной глубине в каждый момент времени одного цвета. Во-вторых, перед нами полное бинарное дерево, поэтому для заданных ограничений высота не превышает 30 + мы умеем легко считать отца вершины. Отсюда решение — можно отвечать на запросы моделированием (поднимаясь к LCA).
Chef and Churu — не знаю, как делать нормально, лень было думать, так как сел за контест в последнюю ночь:) Я упихал корневую. Во-первых, заменим отрезки [L,R] на [1,L-1] и [1,R] — нам нужно просуммировать отрезки первого типа, просуммировать отрезки второго типа, потом вычесть из второго результата первый. Отсортируем эти наши отрезки по правому краю, разобьем на блоки; внутри каждого блока отсортируем по номеру. Теперь для операции изменения в массиве в позиции Х нам важно заметить, что почти во всех блоках либо максимальное значение правого края меньше Х (на эти блоки можно забить), либо минимальное значение правого края не меньше Х (таким блокам делаем + на всем блоке за О(1)). Только один блок может быть "плохим", и его нужно обновить вручную. Для запроса — в каждом блоке у нас все отсортировано по номеру, поэтому мы можем найти в нем границы нашего запроса бинарным поиском. Если прикрутить сюда частичные суммы, то при известных границах можно за О(1) сказать результат в этом блоке. Из хитрых мест — не стоит забывать, что ответ на макс.тест не влезает в long long, поэтому без unsigned long long будет WA на одном из тестов третьей группы.
Chef and Words — у нас есть матрица перехода, возведя ее в нужную степень — можем определить, какая вероятность того, что буква Х перейдет в букву Y через K шагов. Вероятность получить конкретное слово равна произведению вероятностей по каждой из его букв. Единственная хитрость — слова в словаре могут дублироваться:) И для таких слов не нужно прибавлять значение к ответу несколько раз.
Sereja and Permutations — переберем, какая из перестановок была получена после удаления первого числа, и какое это было число. Зафиксировав число х, мы знаем, что среди остальных n-1 перестановок число х-1 должно встречаться на первом месте x-1 раз, все остальные — число х. Если это так, и число нам подходит, то промоделируем действия Сережи для нашей перестановки-кандидата и проверим, совпадает ли результат со входными данными.
Sereja and Order — известная задача теории оптимизации, представитель класса Open Shop Problems. Решение, при желании, можно легко нагуглить:) Если коротко — когда у нас есть свободная машина, то на нее лучше ставить работу, которая еще не выполнялась ни на одной из машин, а если таких работ несколько — ту, у которой максимальная продолжительность выполнения на другой машине. Моделируем все это несколькими сетами, вот и все. На самом деле вводит в заблуждение то, что на странице контеста у задачи мало Successful Submission, но на это не стоит обращать внимание) У той же Chef and Churu полных решений меньше, но все отправляли частичные, а теперь это тоже засчитывается.